Charges +q−4q and +2q are arranged at the corners of an equilatoral triangle of side 0.15m.If the q=1μC their mutual potential energy is
0.4J
0.5J
0.6J
0.8J
The correct Answer is:3
To find the mutual potential energy of the charges arranged at the corners of an equilateral triangle, we can follow these steps:
1. Identify the Charges and Their Values:
- Let the charges be:
- q1=+q=+1μC=+1×10−6C
- q2=−4q=−4×1μC=−4×10−6C
- q3=+2q=+2×1μC=+2×10−6C
2. Determine the Side Length of the Triangle:
- The side length L of the equilateral triangle is given as 0.15m.
3. Use the Formula for Potential Energy Between Two Point Charges:
- The potential energy U between two point charges qi and qj separated by a distance r is given by:
Uij=kqiqjr
- Where k=9×109Nm2/C2 is Coulomb's constant.
4. Calculate the Potential Energy for Each Pair of Charges:
- For q1 and q2:
U12=kq1q2L=9×109(1×10−6)(−4×10−6)0.15
U12=9×109−4×10−120.15=−240×10−3=−0.24J
- For q1 and q3:
U13=kq1q3L=9×109(1×10−6)(2×10−6)0.15
U13=9×1092×10−120.15=120×10−3=0.12J
- For q2 and q3:
U23=kq2q3L=9×109(−4×10−6)(2×10−6)0.15
U23=9×109−8×10−120.15=−480×10−3=−0.48J
5. Calculate the Total Mutual Potential Energy:
- The total potential energy U is the sum of the potential energies of each pair:
U=U12+U13+U23
U=(−0.24)+(0.12)+(−0.48)=−0.60J
Final Answer:
The mutual potential energy of the three charges is U=−0.60J.
- Let the charges be:
- q1=+q=+1μC=+1×10−6C
- q2=−4q=−4×1μC=−4×10−6C
- q3=+2q=+2×1μC=+2×10−6C
- The side length L of the equilateral triangle is given as 0.15m.
- The potential energy U between two point charges qi and qj separated by a distance r is given by:
Uij=kqiqjr
- Where k=9×109Nm2/C2 is Coulomb's constant.
- For q1 and q2:
U12=kq1q2L=9×109(1×10−6)(−4×10−6)0.15
U12=9×109−4×10−120.15=−240×10−3=−0.24J
U13=kq1q3L=9×109(1×10−6)(2×10−6)0.15
U13=9×1092×10−120.15=120×10−3=0.12J
U23=kq2q3L=9×109(−4×10−6)(2×10−6)0.15
U23=9×109−8×10−120.15=−480×10−3=−0.48J
- The total potential energy U is the sum of the potential energies of each pair:
U=U12+U13+U23
U=(−0.24)+(0.12)+(−0.48)=−0.60J
The mutual potential energy of the three charges is U=−0.60J.
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level II(C.W)
Explore 27 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level III (C.W)
Explore 55 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:C.U.Q
Explore 133 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
Three charges +q,+qand−q are located at the corners of an equilaterial triangle of side a. Calculate potential energy of the system.
View SolutionThree charges +q,2qand−4q are placed on the three vertices of an equale-laterail triangle of each side0⋅1m. Calculate electrostatic potential energy of the system, take q=10−7C
View Solution
Knowledge Check
Three charges each20μC are placed at the corners of an equilateral triangle of side 0.4m The potential energy of the system is
A18×10−6JB9JC9×10−6JD27JThree point charges of +2q,+2qand−4q are placed at the corners A, B and C of an equilateral triangle ABC of side x. The magnitude of the electric dipole moment of this system is
A2 qxB3√2qxC3 qxD2√3qxThree point charges of +2q,+2qand−4q are placed at the corners A, B and C of an equilateral triangle ABC of side x. The magnitude of the electric dipole moment of this system is
A2qxB3√2qxC3qxD2√3qx
Three charges -q +q and +q are placed at the corner of the equilateral triangle of side a as shown in the figure.The net electric potential at the centroid of the triangle will be (k=(1)/(4 pi varepsilon_(0)))
View SolutionElectric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work done to separate the charges at infinite distance.

View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View SolutionThree charges of (+2q),(−q) and (−q) are placed at the corners A,B and C of an equilateral triangle of side a as shown in the adjoining figure. Then the dipole moment of this combination is
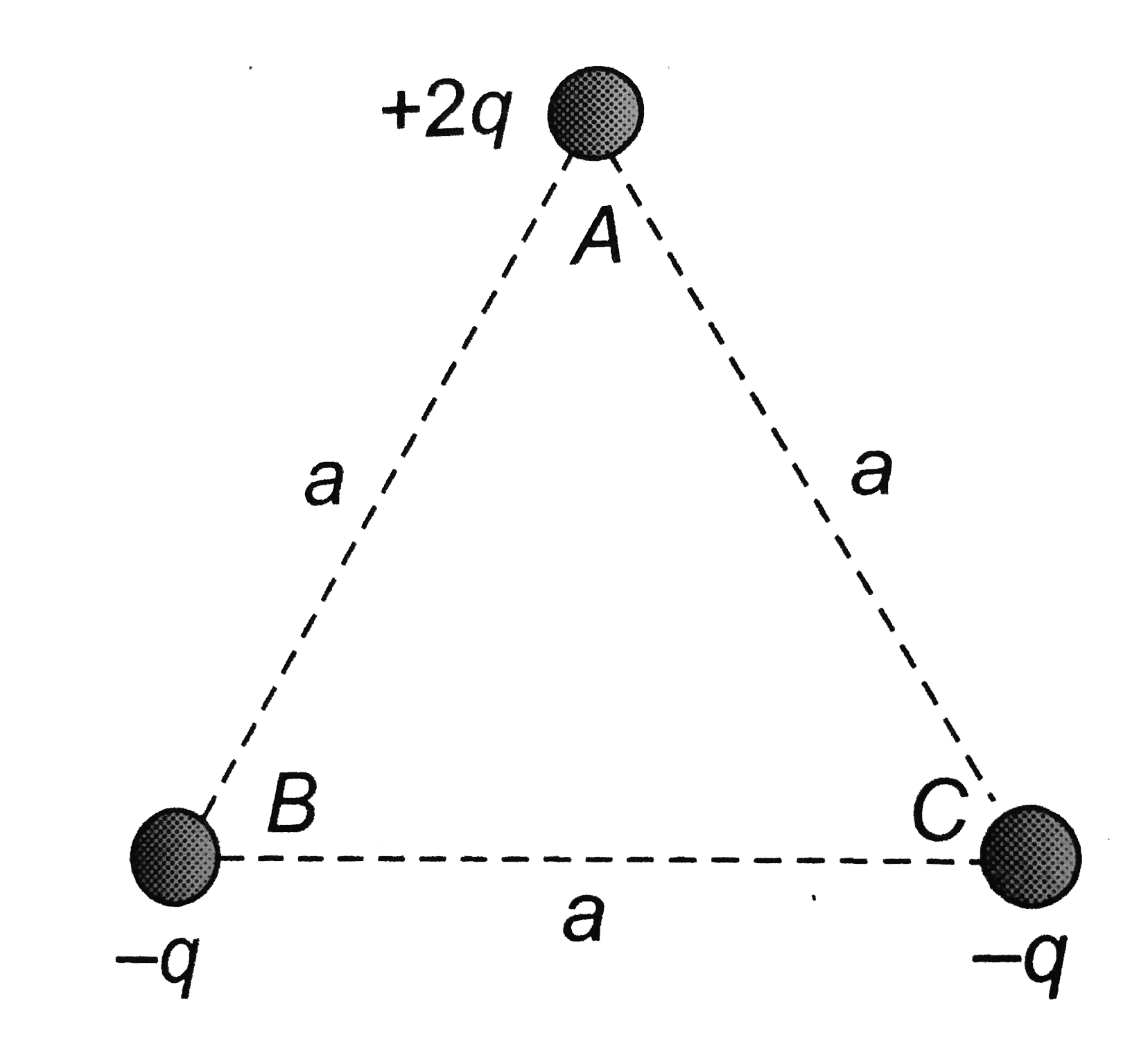
View Solution

