A charge of +2μC is placed at x=0 and a charge of −32μc at x=60 .A third charge −Q be placed on the x axis such that it experiences no force .The distance of the point from +2μC is ( in cm)
−20
20
15
10
The correct Answer is:1
To solve the problem, we need to find the position along the x-axis where a charge of −Q can be placed such that it experiences no net force due to the other two charges, +2μC at x=0 and −32μC at x=60 cm.
1. Understand the Setup:
- We have two charges:
- Charge Q1=+2μC at x=0 cm.
- Charge Q2=−32μC at x=60 cm.
- We need to place a third charge Q3=−Q at a position x=d such that the net force on it is zero.
2. Determine the Regions:
- The charge Q3 can be placed in three possible regions:
- To the left of Q1 (i.e., x<0)
- Between Q1 and Q2 (i.e., 0<x<60)
- To the right of Q2 (i.e., x>60)
Since Q3 is negative, it will experience a repulsive force from Q1 and an attractive force from Q2. The only region where it can experience no net force is to the left of Q1.
3. Set Up the Electric Field Equations:
- The electric field E1 due to Q1 at a distance d is given by:
E1=kQ1d2=k2×10−6d2
- The electric field E2 due to Q2 at a distance d+60 (since Q2 is at 60 cm) is given by:
E2=k|Q2|(d+60)2=k32×10−6(d+60)2
4. Set the Electric Fields Equal:
- For the charge Q3 to experience no net force, the magnitudes of the electric fields must be equal:
E1=E2
- Therefore, we have:
k2×10−6d2=k32×10−6(d+60)2
- The k cancels out:
2d2=32(d+60)2
5. Cross-Multiply and Simplify:
- Cross-multiplying gives:
2(d+60)2=32d2
- Expanding the left side:
2(d2+120d+3600)=32d2
- Simplifying:
2d2+240d+7200=32d2
- Rearranging:
30d2−240d−7200=0
6. Solve the Quadratic Equation:
- Dividing the entire equation by 30:
d2−8d−240=0
- Using the quadratic formula d=−b±√b2−4ac2a:
d=8±√(−8)2−4⋅1⋅(−240)2⋅1
d=8±√64+9602
d=8±√10242
d=8±322
- This gives two solutions:
d=402=20andd=−242=−12
7. Select the Valid Solution:
- Since we are looking for a position to the left of Q1, we take d=−12 cm.
- Thus, the distance from +2μC is 12 cm to the left.
Final Answer:
The distance of the point from +2μC is 12 cm (to the left).
- We have two charges:
- Charge Q1=+2μC at x=0 cm.
- Charge Q2=−32μC at x=60 cm.
- We need to place a third charge Q3=−Q at a position x=d such that the net force on it is zero.
- The charge Q3 can be placed in three possible regions:
- To the left of Q1 (i.e., x<0)
- Between Q1 and Q2 (i.e., 0<x<60)
- To the right of Q2 (i.e., x>60)
- The electric field E1 due to Q1 at a distance d is given by:
E1=kQ1d2=k2×10−6d2
- The electric field E2 due to Q2 at a distance d+60 (since Q2 is at 60 cm) is given by:
E2=k|Q2|(d+60)2=k32×10−6(d+60)2
- For the charge Q3 to experience no net force, the magnitudes of the electric fields must be equal:
E1=E2
- Therefore, we have:
k2×10−6d2=k32×10−6(d+60)2
- The k cancels out:
2d2=32(d+60)2
- Cross-multiplying gives:
2(d+60)2=32d2
- Expanding the left side:
2(d2+120d+3600)=32d2
- Simplifying:
2d2+240d+7200=32d2
- Rearranging:
30d2−240d−7200=0
- Dividing the entire equation by 30:
d2−8d−240=0
- Using the quadratic formula d=−b±√b2−4ac2a:
d=8±√(−8)2−4⋅1⋅(−240)2⋅1
d=8±√64+9602
d=8±√10242
d=8±322
- This gives two solutions:
d=402=20andd=−242=−12
- Since we are looking for a position to the left of Q1, we take d=−12 cm.
- Thus, the distance from +2μC is 12 cm to the left.
The distance of the point from +2μC is 12 cm (to the left).
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level II(C.W)
Explore 27 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level III (C.W)
Explore 55 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:C.U.Q
Explore 133 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
Two charges Q and -3Q are placed fixed on x-axis separated by a distance 'd' Where should a third charge 2Q be placed such that it will not experience any force?
View SolutionTwo charge q and –3q are placed fixed on x–axis separated by distance d. Where should a third charge2q be placed such that it will not experience any force ?
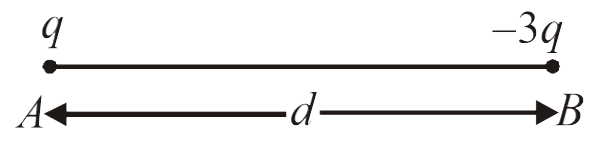
View Solution
Knowledge Check
Two charges q and −3q are placed fixed on x-axis separated by distance d. Where should a third charge 2q be placed such that it will not experience any force ?
Ad2(1+√3) to the left of qBd2(1+√3) tothe right of qCd2(1+√5) to the left of qDd2(1+√5) to the right of qA charge q=−2.0μC is placed at origin. Find the electric field at (3m,4m,0).
A−(4.32ˆi+5.76ˆj)×102N/CB−(4.32ˆi−5.76ˆj)×102N/CC−(5.76ˆi+4.32ˆj)×102N/CD(4.32ˆi+5.76ˆj)×102N/CThe number of lines of force starting from a point charge of 10μC in vacuum are
A1.2×106Nm2/CB1.3×106Nm2/CC1.13×106Nm2/CD2.3×106Nm2/C
Two charge q and –3q are placed fixed on x–axis separated by distance d. Where should a third charge2q be placed such that it will not experience any force ?

View SolutionTwo charges q and 3q are placed fixed on x-axis separated by distance 'd'. Where should a third charge 2q be placed such that it will not experience any force ?
View SolutionA point charge q1=+2μC is placed at the origin of coordinates. A second charge, q2=−3μC, is placed on the x-axis at x=100cm. At what point (or points) on the x-axis will the absolute potential be zero?
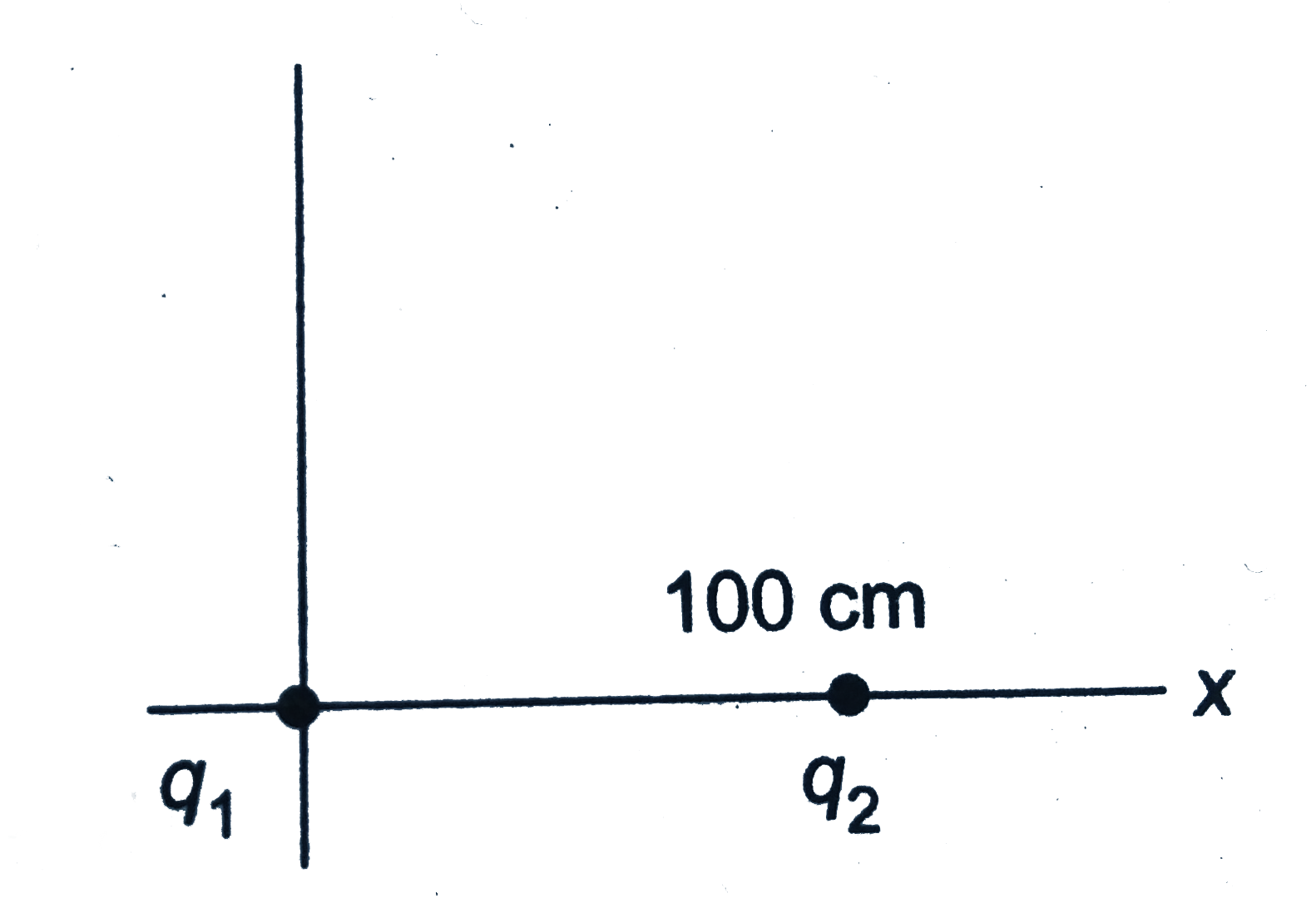
View SolutionTwo free charges q and 4q are placed at a distance d apart A third charge Q is placed between them at a distance x from charge q such that the system is in equilibrium. Then magnitude of third charge and postion,
View SolutionEqual charges each of 20μC are placed at x=0,2,4,8,16cm on X-axis. Find the force experienced by the charge at x=2cm.
View Solution

