A thin fixed ring of radius a has a positive charge q uniformly distributed over it.A particle of mass m having a negative charge Q, is placed on the axis at a distance of x(x<<a) form the center of the ring. Show that the motion of the negatively charged particle is approximately simple harmonic. Calculate the time period of oscillation.

The force on thepoint charge Q due to the element dq of the ring is
F=14πε0dQr2 along AB
For every element of the ring ,there is symmetrcially situated diametrically oppsite element ,the components of froces along the axis will add up while those perpendicular to it will cancel each other .Hence, net force on the charge −Q is −ve sign shows that this force will be towards the centre of ring.
F=∫dFcosθ=cosθ∫dF
=xF∫14πε0[−Qdqr2]
F=−14πε0Qrr3∫dq=−14πε0Qqx(a2+x2)32....(1)
(as r=(a2+x2)12 and r=(a2+x2)12)
As the resorting froce is not linerar ,so the motion will be oscillatory .However if x<<a then
F=−14πε0Qqa3x=−kx
with k=Qq4πε0a3
i.e, the restoring force will become linear and so the motion is simple harmonic with time period.
T=2πω=2π√mk=2π√4πε0ma3qQ
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - C.U.Q
133 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 1(C.W)
24 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS
14 Videos
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type
6 Videos
Similar Questions
A thin fixed ring of radius a has a positive chage q unformly distributed over it.A particle of mass m having a megative charge Q, is placed on the axis at a distance of x(x<<a) form the center of the ring. Show that the motion of the negatively chaged particle is approximatly simple harmonic. Calculate the time period of oscillation.

View SolutionA thin fixed of radius 1 metre has a positive charge 1×10−5 coulomb uniformly distributed over it. A particle of mass 0.9 gm and having a negative charge of 1×10−6 coulomb is placed on the axis at a distance of 1cm from the centre of the ring. Show that the motion of the negatively charged particle is approaximately simple harmonic. Calculate the time period of oscillations.
View Solution
Knowledge Check
A thin semi-circular ring of radius r has a positive charge q distributed uniformly over it. The net field →E at the centre O is
 A(a) q4π2ε0r2ˆjB(b) −q4π2ε0r2ˆjC(c) −q2π2ε0r20ˆjD(d) q2π2ε0r2ˆj
A(a) q4π2ε0r2ˆjB(b) −q4π2ε0r2ˆjC(c) −q2π2ε0r20ˆjD(d) q2π2ε0r2ˆjA thin semi-circular ring of radius r has a positive charge q distributed uniformly over it as shown in the figure. The net field →E at the center O is
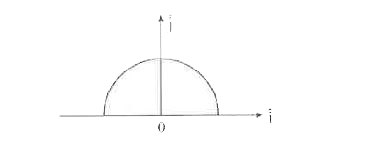 Aq2π2ε0r2ˆjBq4π2ε0r2ˆjC−q2π2ε0r2ˆjD−q2π2ε0r2ˆj
Aq2π2ε0r2ˆjBq4π2ε0r2ˆjC−q2π2ε0r2ˆjD−q2π2ε0r2ˆjA positive charge Q is uniformly distrubuted along a circular ring of radius R.a small test chage q is placed at the centre of the ring .The
 Aif q>0 and is displaced away from the centre in the plane of the ring.it will be pushed back towards the centre.Bif q<0 and is displaced away from the cnetre in the plane of the ring .it will never return to the centre and will continue moving till it hits the ring.Cif q<0 it will perform SHM for small displacement along the axisDq at the centre of the ring is in an unstable equilibrium within the plane of the ring for q<0
Aif q>0 and is displaced away from the centre in the plane of the ring.it will be pushed back towards the centre.Bif q<0 and is displaced away from the cnetre in the plane of the ring .it will never return to the centre and will continue moving till it hits the ring.Cif q<0 it will perform SHM for small displacement along the axisDq at the centre of the ring is in an unstable equilibrium within the plane of the ring for q<0
Electric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x ltltR, find the time period of oscillation of the particle if it is released from there.
View SolutionA ring of radius R carries a uniformly distributed charge +Q. A point charge −q is placed on the axis of the ring at a distance 2R from the centre of the ring and released from rest. The particle executes a ismple harmonic motion along the axis of the ring.
View SolutionA conducting ring of radius 40 cm has a charge of 5×10−9 C uniformly distributed over it. Calculate the electric field intensity at a point P, 40 cm away from the centre on the axis of the ring.
View SolutionFind the electric flux due to a point charge 'Q' through the circular region of radius R if the charge is placed on the axis of ring at a distance x.
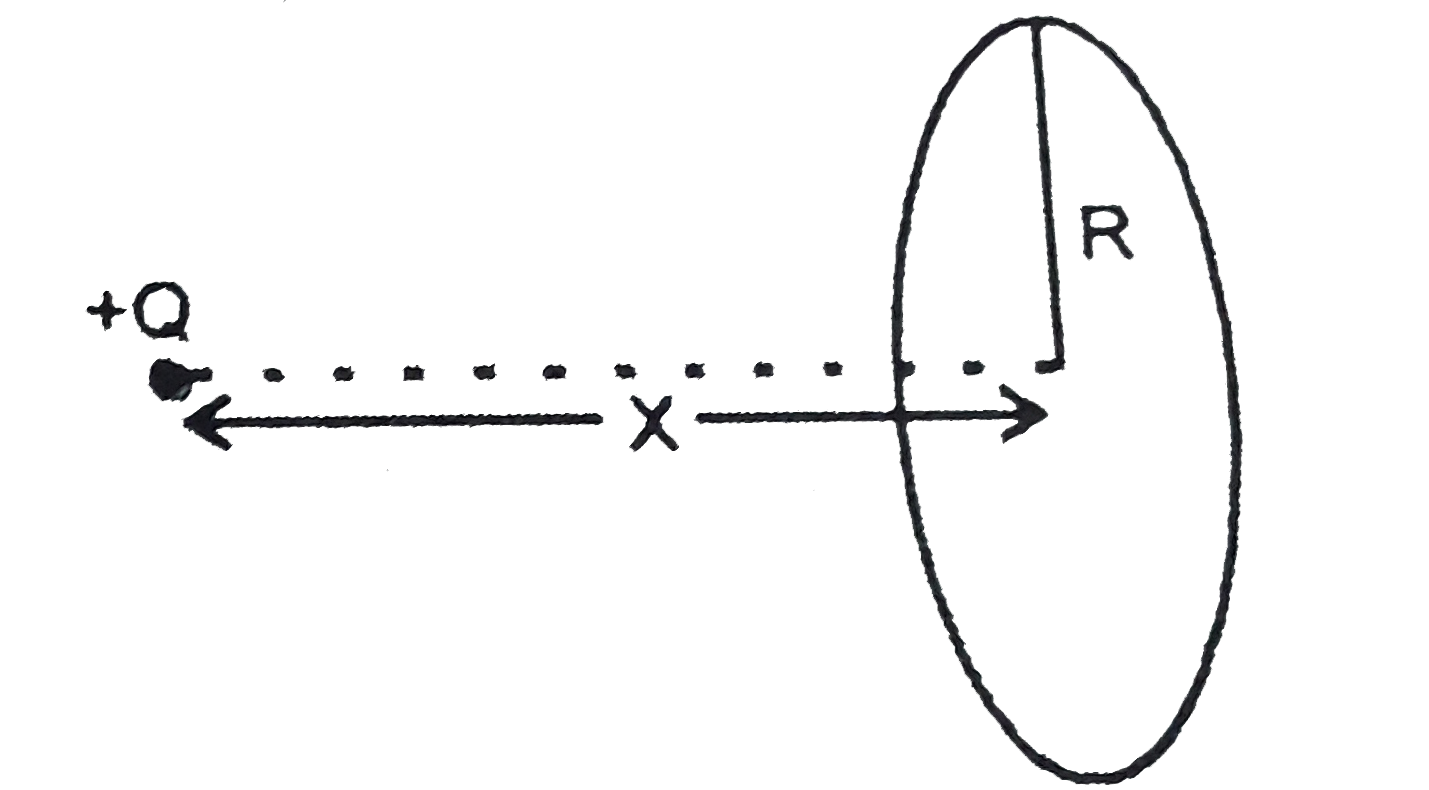
View Solution
