A circular current-carrying coil has a radius R. The distance from the centre of the coil, on the axis, where B will be 1/8 of its value at the centre of the coil is
R√3
√3R
2√3R
2R√3
The correct Answer is:B
To solve the problem of finding the distance from the center of a circular current-carrying coil on its axis where the magnetic field B is 18 of its value at the center, we can follow these steps:
Step 1: Understand the Magnetic Field at the Center and on the Axis
The magnetic field at the center of a circular coil is given by the formula:
Bc=μ0I2R
where μ0 is the permeability of free space, I is the current flowing through the coil, and R is the radius of the coil.
The magnetic field at a distance x along the axis of the coil is given by:
Ba=μ0IR22(R2+x2)3/2
Step 2: Set Up the Equation
According to the problem, we want to find the distance x such that:
Ba=18Bc
Substituting the expressions for Ba and Bc:
μ0IR22(R2+x2)3/2=18(μ0I2R)
Step 3: Simplify the Equation
Canceling μ0I from both sides:
R22(R2+x2)3/2=116R
Cross-multiplying gives:
16R⋅R2=2(R2+x2)3/2
This simplifies to:
16R3=2(R2+x2)3/2
Dividing both sides by 2:
8R3=(R2+x2)3/2
Step 4: Take the Cube Root
Taking the cube root of both sides:
(8R3)1/3=R2+x2
This simplifies to:
2R=R2+x2
Step 5: Rearrange the Equation
Rearranging gives:
x2=2R−R2
Step 6: Solve for x
Thus:
x=√2R−R2
Factoring out R:
x=√R(2−R)
Step 7: Find the Value of x in Terms of R
To express x in a simpler form, we can use the identity:
x=R√2−R
However, we need to find the specific value of x that corresponds to the condition given in the problem.
Conclusion
After solving, we find that:
x=R√3
Thus, the distance x from the center of the coil on the axis where the magnetic field is 18 of its value at the center is:
x=R√3
The magnetic field at the center of a circular coil is given by the formula:
Bc=μ0I2R
where μ0 is the permeability of free space, I is the current flowing through the coil, and R is the radius of the coil.
Ba=μ0IR22(R2+x2)3/2
According to the problem, we want to find the distance x such that:
Ba=18Bc
Substituting the expressions for Ba and Bc:
μ0IR22(R2+x2)3/2=18(μ0I2R)
Canceling μ0I from both sides:
R22(R2+x2)3/2=116R
Cross-multiplying gives:
16R⋅R2=2(R2+x2)3/2
This simplifies to:
16R3=2(R2+x2)3/2
Dividing both sides by 2:
8R3=(R2+x2)3/2
Taking the cube root of both sides:
(8R3)1/3=R2+x2
This simplifies to:
2R=R2+x2
Rearranging gives:
x2=2R−R2
Thus:
x=√2R−R2
Factoring out R:
x=√R(2−R)
To express x in a simpler form, we can use the identity:
x=R√2−R
However, we need to find the specific value of x that corresponds to the condition given in the problem.
After solving, we find that:
x=R√3
Thus, the distance x from the center of the coil on the axis where the magnetic field is 18 of its value at the center is:
x=R√3
Topper's Solved these Questions
Similar Questions
A circular current carrying coil has a radius R. The distance from the centre of the coil on the axis where the magnetic induction will be 18 th to its value at the centre of the coil, is
View SolutionA circular current carrying coil has a radius a. Find the distance from the centre of coil, on its axis, where is the magnetic induction will be 1/6th of its value at the centre of coil.
View Solution
Knowledge Check
A circular current carrying coil has a radius R. The distance from the centre of the coil on the axis where the magnetic induction will be (1/8)th of its value at the centre of the coil, is
AR/√3BR√3C2R/√3D(2R/√3)RThe radius of la circular current carrying coil is R. At what distance from the centre of the coil on its axis, the intensity of magnetic field will be 12√2 times that at the centre?
A2RB3R2CR is doubledDR2Radius of current carrying coil is 'R'. Then ratio of magnetic fields at the centre of the coil to the axial point, which is R√3 distance away from the centre of the coil :-
A1:1B1:2C1:4D8:1
Show that the magnetic field along the axis of a current carrying coil of radius r at a distance x from the centre of the coil is smaller by the fraction 3x2/2r2 than the field at the centre of the coil carrying current.
View SolutionAn electric current is flowing in a circular coil of radius r .If at a distance √Kr from the centre on the axis of the coil the magnetic fleld be 18 th of it's value at the centre,then find the value of K.
View SolutionA closely wound, circular coil with radius 2.40cm has 800 turns.
(a) What must the current in the coil be if the magnetic field at the centre of the coil is0.0580T?
(b) At what distance x from the centre of the coil, on the axis of the coil, is the magnetic field half its value at the centre?
View Solution(a) A circular current carrying coil has a radius R. Find magnetic field (a) at centre and (b) along the axis of coil distant √3R from centre. The coil is having N turns and carriers a current i.
(b) Two concentric coil A and B, having current i and 2i and radii 2R and R are placed as shown. Find magnetic field at common centre.
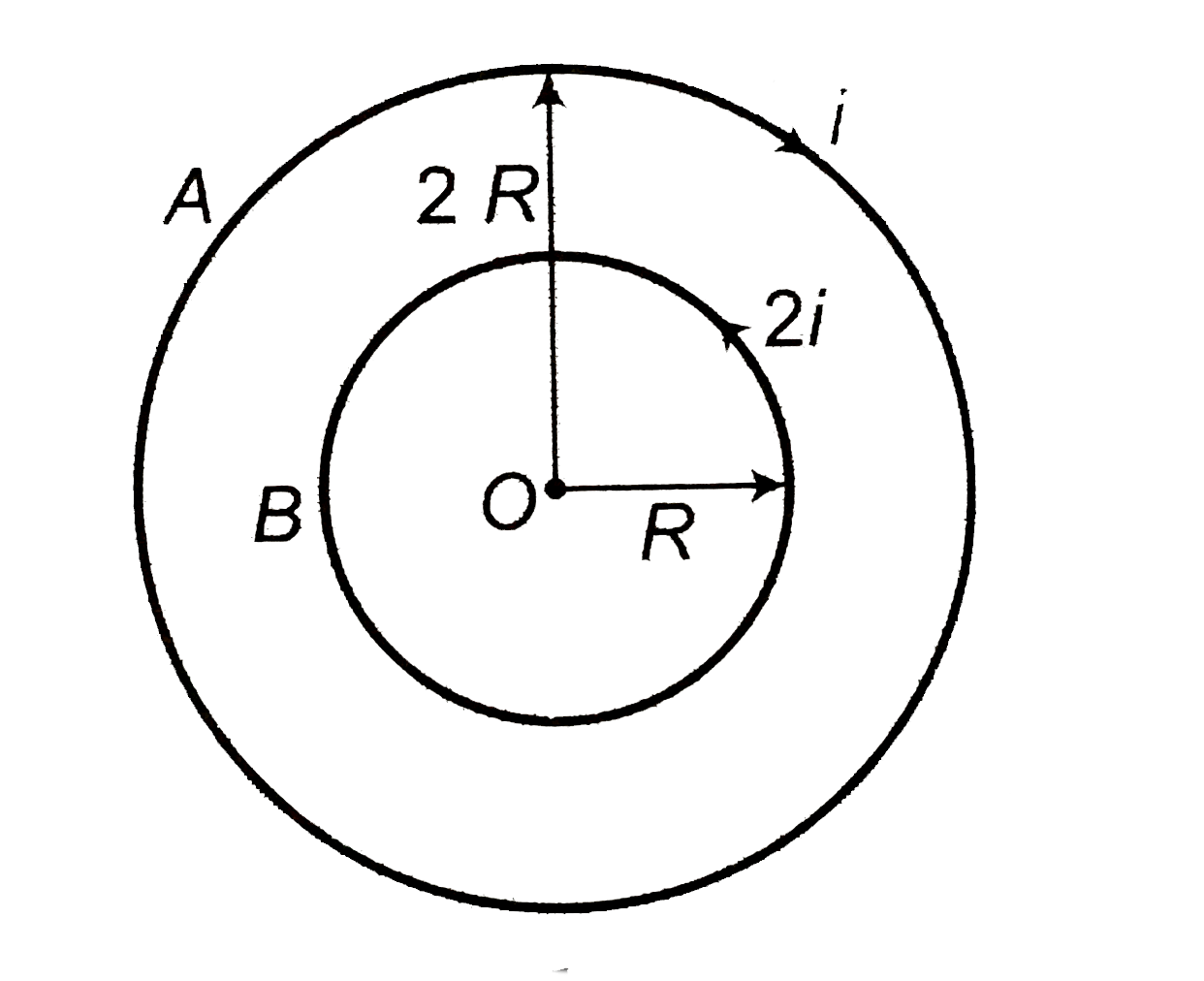
(c) In previous problem, if planes of coil are perpendicular to each other, find magnetic field at common centre.
(d) A charge q distributed uniformely over a circular ring of radius R. The ring rotates about its axis with an angular velocity ω. find the magnetic field (a) at centre and (b) at distance √3R from centre, along the axis.
View SolutionThe ratio of the magnetic field at the centre of a current carrying coil of the radius a and at distance 'a' from centre of the coil and perpendicular to the axis of coil is
View Solution

