A charge of (3.14×10−6) C is distributed uniformly over a circular ring of radius 20.0 cm. The ring rotates about its axis with an angular velocity of 60.0 rads−1 . Find the ratio of the electric field to the magnetic field at a point on the axis at a distance of 5.00 cm from the centre.
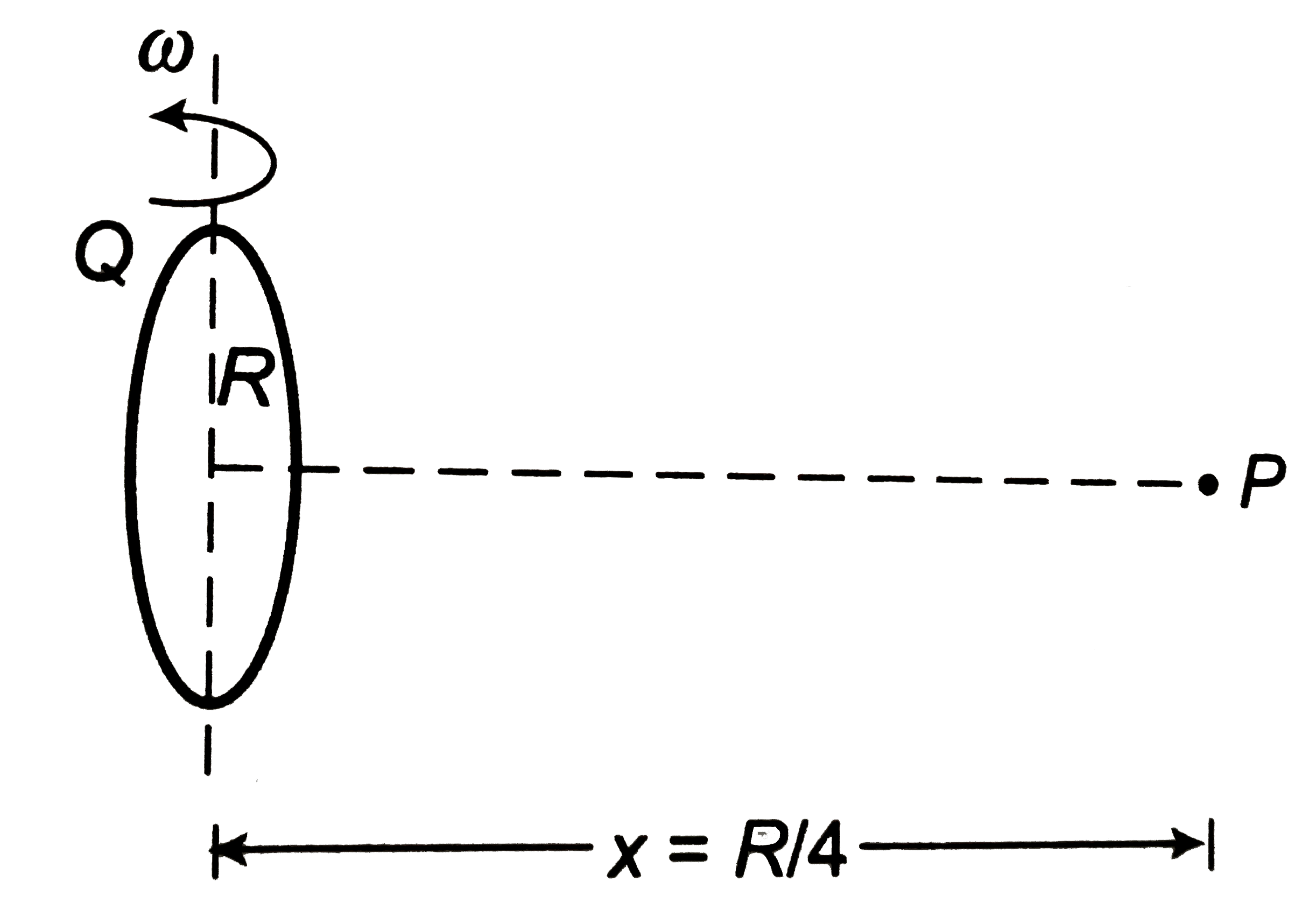
Current due to rotation of charge
i=QT=Q2π/ω=Qω2π
At P:
E=14πε0Qx(R2+x2)3/2
B=μ0iR22(R2+x2)3/2=μ0QωR24π(R2+x2)3/2
EB=1μ0ε0.xωR2
=c2(R/4)ωR4.c: speed of light
=c24ωR=(3×108)24×60×0.2=9×101648
=1.88×1015m/sec
Topper's Solved these Questions
Similar Questions
A thin uniformly charged ring of radius a=10cm rotates about its axsi with an angluaar velocity ω=100rad/s. Find the ratio of volume energy densities of magnetic and electric fields on the axis of the ring at a point removed from its centre by a distance l=a
View SolutionA solenoid of length 10 cm and radius 1 cm contains 200 turns and carries a current of 10 A. Find the magnetic field at a point on the axis at a distance of 10cm from the centre.
View Solution
Knowledge Check
A ring of radius 0.5 m and mass 10 kg is rotating about its diameter with angular velocity of 20 rad/s. Its KE is :-
A10JB100JC500JD250JA ring of radius 0.5 m and mass 10 kg is rotating about its diameter with angular velocity of 20 rad/s. Its KE is :-
A10JB100JC500JD250JA uniformly charged ring of radius R is rotated about its axis with constant linear speed v of each of its particle. The ratio of electric field to magnetic field at a point P on the axis of the ring distant x=R from centre of ring is (c is speed of light )
 Ac2vBv2cCvcDcv
Ac2vBv2cCvcDcv
A charge of 500 μC is distributed uniformly over the circumference of a ring of radius 25 cm. What will be be electric potential at the centre of ring?
View SolutionA uniformly charged ring of radius 0.1m rotates at a frequency of 104rps about its axis.Find the ratio of energy density of electric field to the energy density of the magnetic field at a point on the axis at distance 0.2m from the centre.(Use speed of light c=3×108m/s,π2=10)
View Solution(a) A circular current carrying coil has a radius R. Find magnetic field (a) at centre and (b) along the axis of coil distant √3R from centre. The coil is having N turns and carriers a current i.
(b) Two concentric coil A and B, having current i and 2i and radii 2R and R are placed as shown. Find magnetic field at common centre.
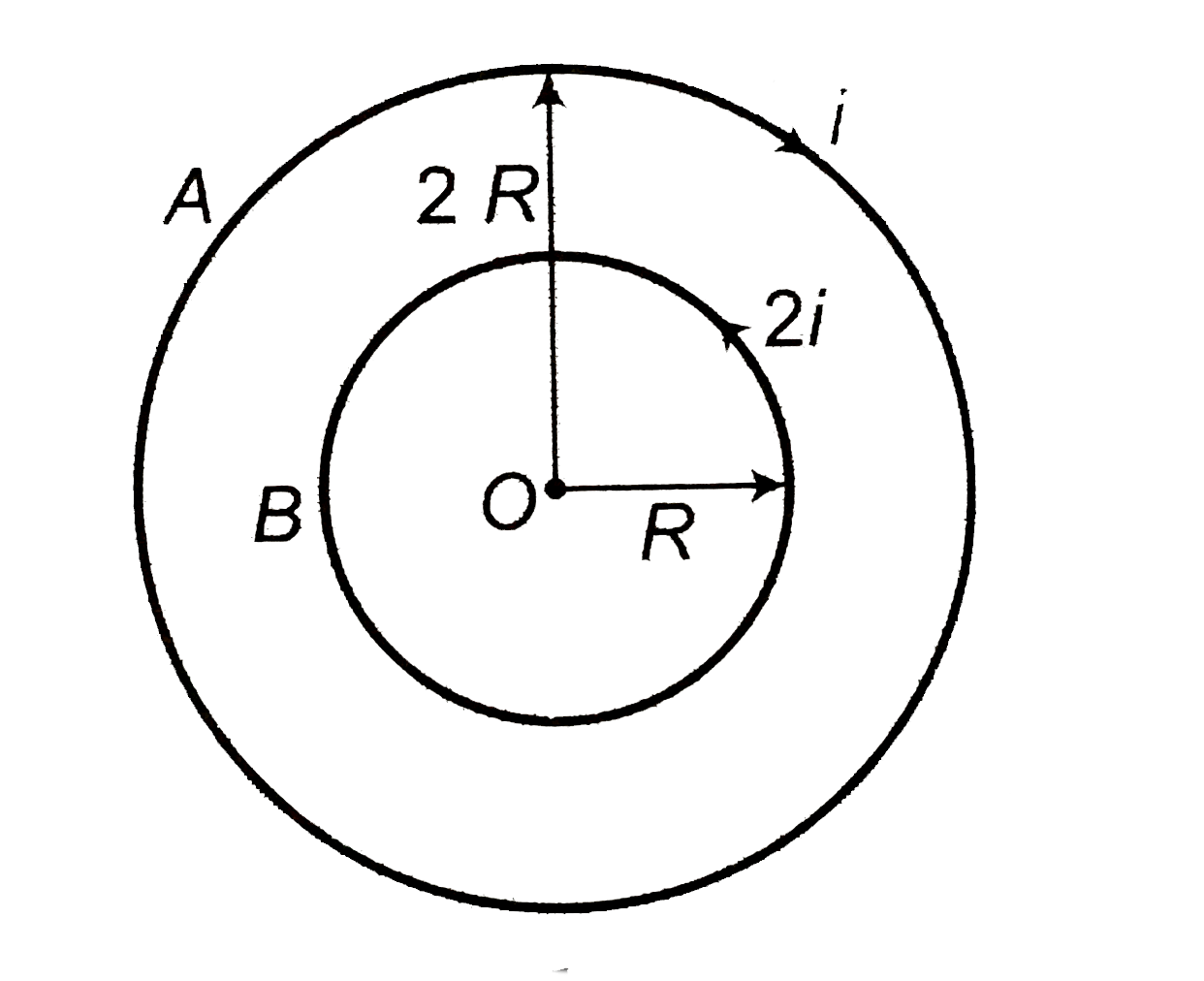
(c) In previous problem, if planes of coil are perpendicular to each other, find magnetic field at common centre.
(d) A charge q distributed uniformely over a circular ring of radius R. The ring rotates about its axis with an angular velocity ω. find the magnetic field (a) at centre and (b) at distance √3R from centre, along the axis.
View SolutionThe magnetic field B due to a current carrying circular loop of radius 12cm at its centre is 0.5×10−4T. Find the magnetic field due to this loop at a point on the axis at a distance of 5.0cm from the centre.
View SolutionA charge q is spread uniformly over an isolated ring of radius 'R'. The ring is rotated about its natural axis and has magnetic dipole moment of the ring as M. Angular velocity of rotation is
View Solution
