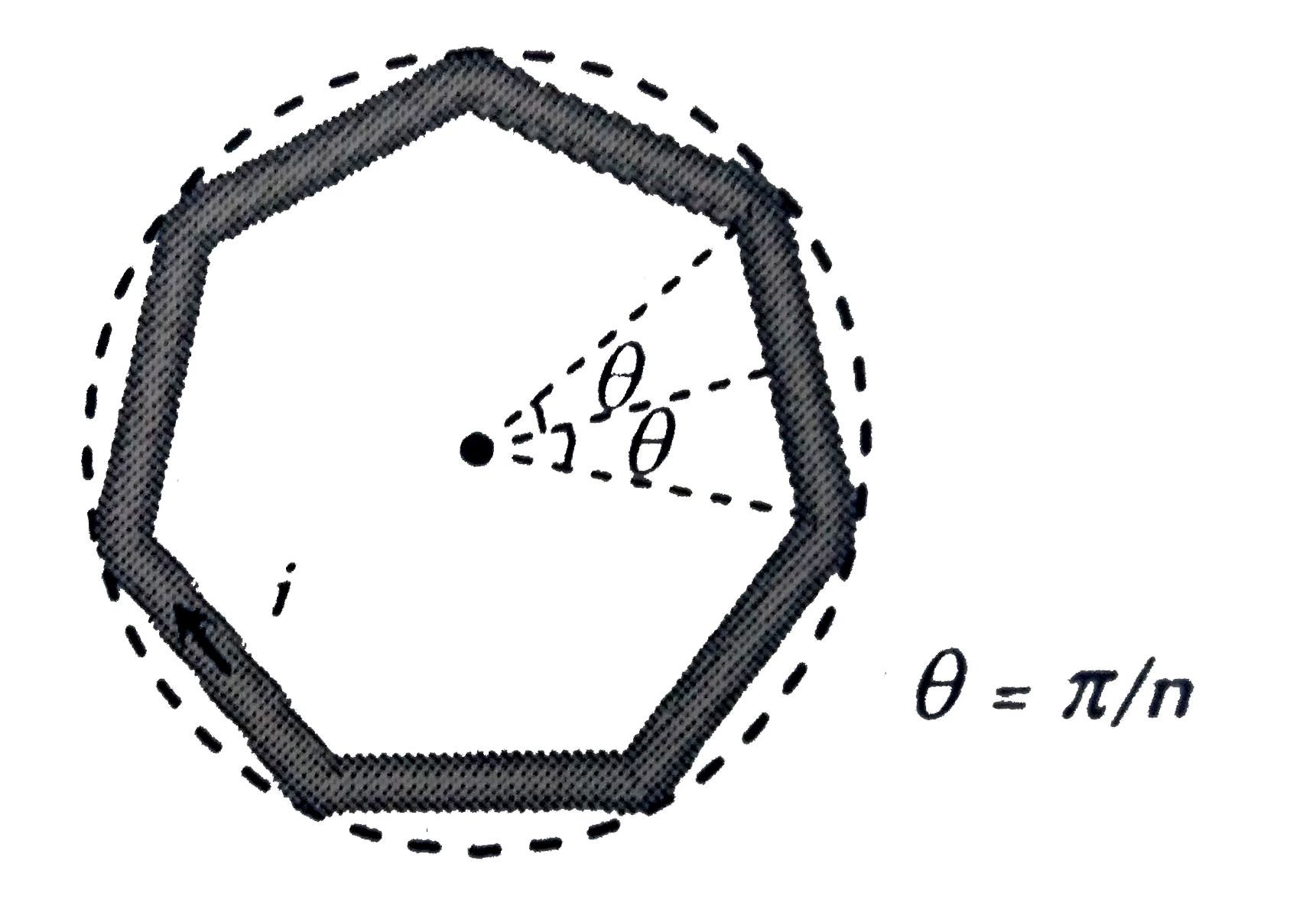
A current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic fiedl induction at the center of polygon due to one side of the polygon is

Video Solution

Text Solution

Verified by Experts

Angle subtended by one side at centre $= 2 π / n$
$d = R cos (π / n)$
Magnetic field at $O$ due to one side
$B_{1} = \frac{μ_{0} i}{4 π d} (sin . \frac{π}{n} + sin . \frac{π}{n})$
$= \frac{μ_{0} i}{4 π . R . cos (\frac{π}{n})} .2 sin (\frac{π}{n})$
$= \frac{μ_{0} tan (π / n)}{2 π R}$
Magnetic field due to polygon
$B_{O} = n B_{1} = \frac{μ_{0} n i tan (π / n)}{2 π R}$
when $n \to \infty$ , polygon becomes circle
$B_{O} = \frac{μ_{0} i}{2 R}$

Updated on:21/07/2023

In the following figure a wire bent in the form of a regular polygon of $n$ sides is inscribed in a circle of radius $a$ . Net magnetic field at centre will be

A $\frac{μ_{0} i}{2 π a} tan \frac{π}{n}$
B $\frac{μ_{0} n i}{2 π a} tan \frac{π}{n}$
C $\frac{2}{π} \frac{n i}{a} μ_{0} tan \frac{π}{n}$
D $\frac{n i}{2 a} μ_{0} tan \frac{π}{n}$
A current I flows in a thin wire in the shape of a regular polygon n sides. The magnetic induction at the centre of the polygon when $n \to \infty$ is (R is the radius of its circumcircle)
A $\frac{μ_{0} n i}{2 π R} tan \frac{π}{6}$
B $\frac{μ_{0} n i}{2 π R} tan \frac{π}{R}$
C $\frac{μ_{0} i}{2 R}$
Dzero
The limit of the interior angle of a regular polygon of n sides as $n \to \infty$ is
A $π$
B $\frac{π}{3}$
C $\frac{3 π}{2}$
D $\frac{2 π}{3}$