A current flows radius along a lengthy thin-walled tube of radisu with longiitual slit of width . Find the induction of the magnietic field inside the tube under the condition

Current flowing in wire of width
Magnetic field due to this wire at centre
Net magnetic field by other wires will be zero.
Topper's Solved these Questions
Similar Questions
A current I flows radius along a lengthy thin-walled tube of radisu R with longiitual slit of width h. Find the induction of the magnietic field inside the tube under the condition h<<R
View SolutionA current I flows in a long straight wire whose cross section is in the shape of a thin quarter ring of radius R. Find the induction of the magnetic field (B) at point O on the axis.

View Solution
Knowledge Check
A long copper tube of inner radius R carriers a current i. The magnetic field B inside the tube is
Aμ0i2πRBμ0i4πRCμ0i2RDZeroCurrent flows through a straight, thin-walled tube of radius r. The magnetic field at a distance x from the axis of the tube has magnitude B.
AB∝x, for 0 lt x lt rBB∝1/x , for 0 lt x lt rCB=0 , for 0≤x<rDB=0 , only for x=0A current I ampere flows along an infinitey1 along straight thin walled tube, then the magnetic induction at any point inside the tube is .
AinfiniteBzeroCμ04π.2irteslaD2irtesla
A current I flows in a long straight wire with cross-section haviing the form of a thin half-ring of radius R (Fig). Find the induction of the magnitude field at the point O.

View SolutionA current I flows along a thin-walled, long, half-cylinder of radius R(figure) Find the magnetic induction at a point on the axis of the cylinder
View SolutionA current I flows in a long thin walled cylinder of radius R. What pressure do the walls of the cylinder experience ?
View SolutionA thin but long, hollow, cylindrical tube of radius r carries a current i along its length. Find the magnitude of the magnetic field at a distance r/2 from the surface (a) inside the tube (b) outside the tube.
View SolutionA current I flows along a thin wire shaped as shown in figure. The radius of the curved part of the wire is r. The field at the centre O of the coil is:
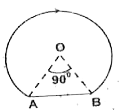
View Solution
