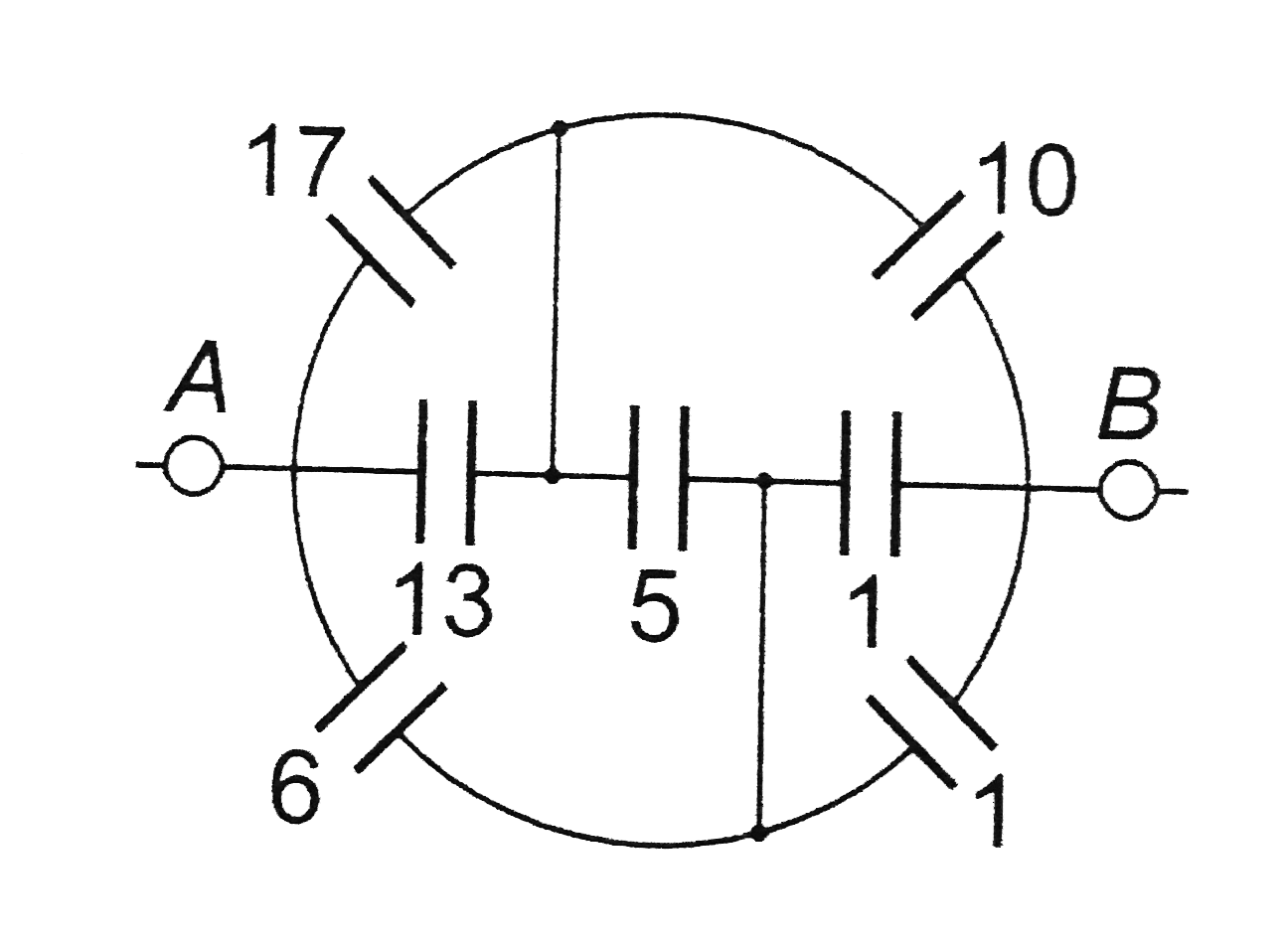
Find the potential difference and caharge on each capacitences. All capacitance in μF.
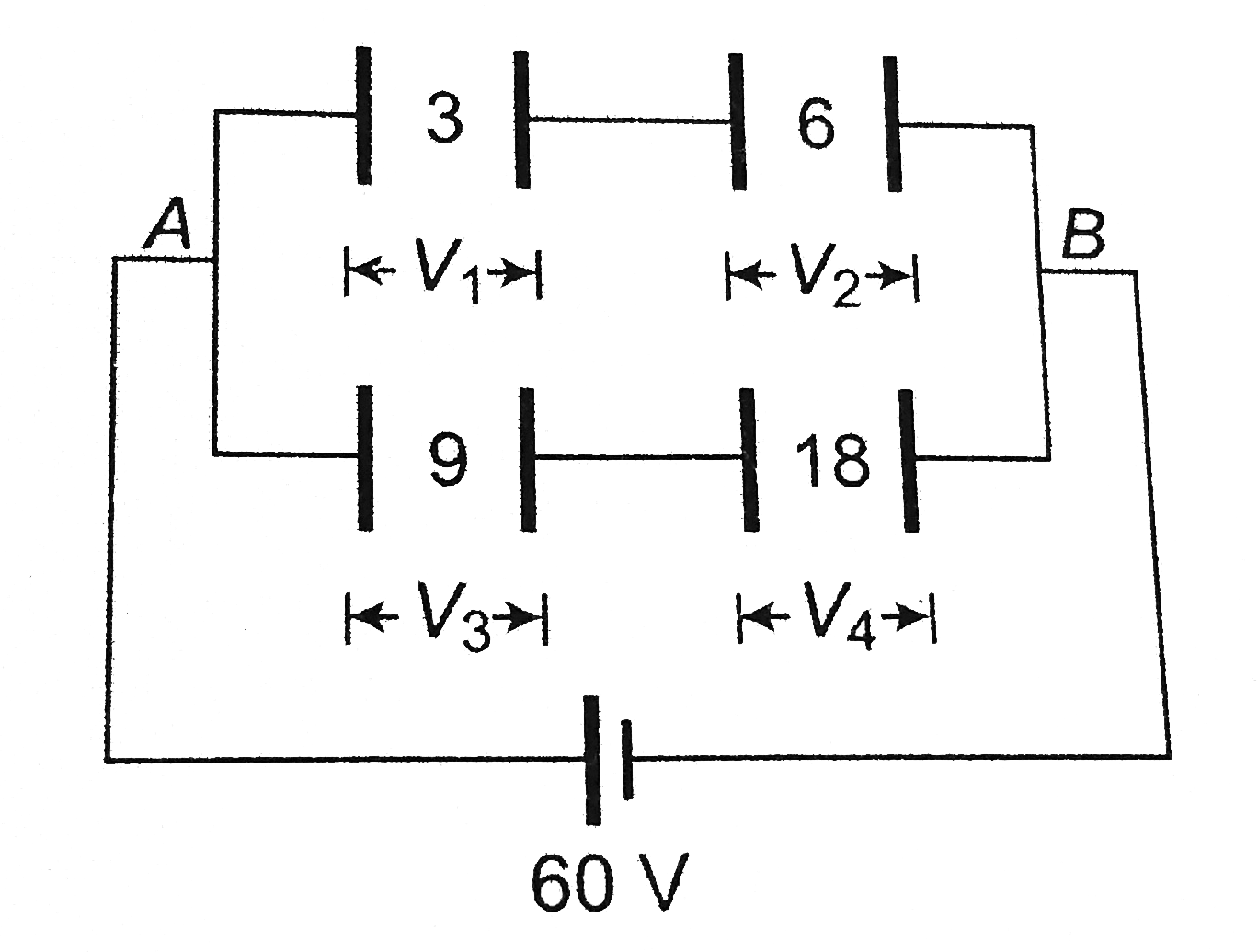
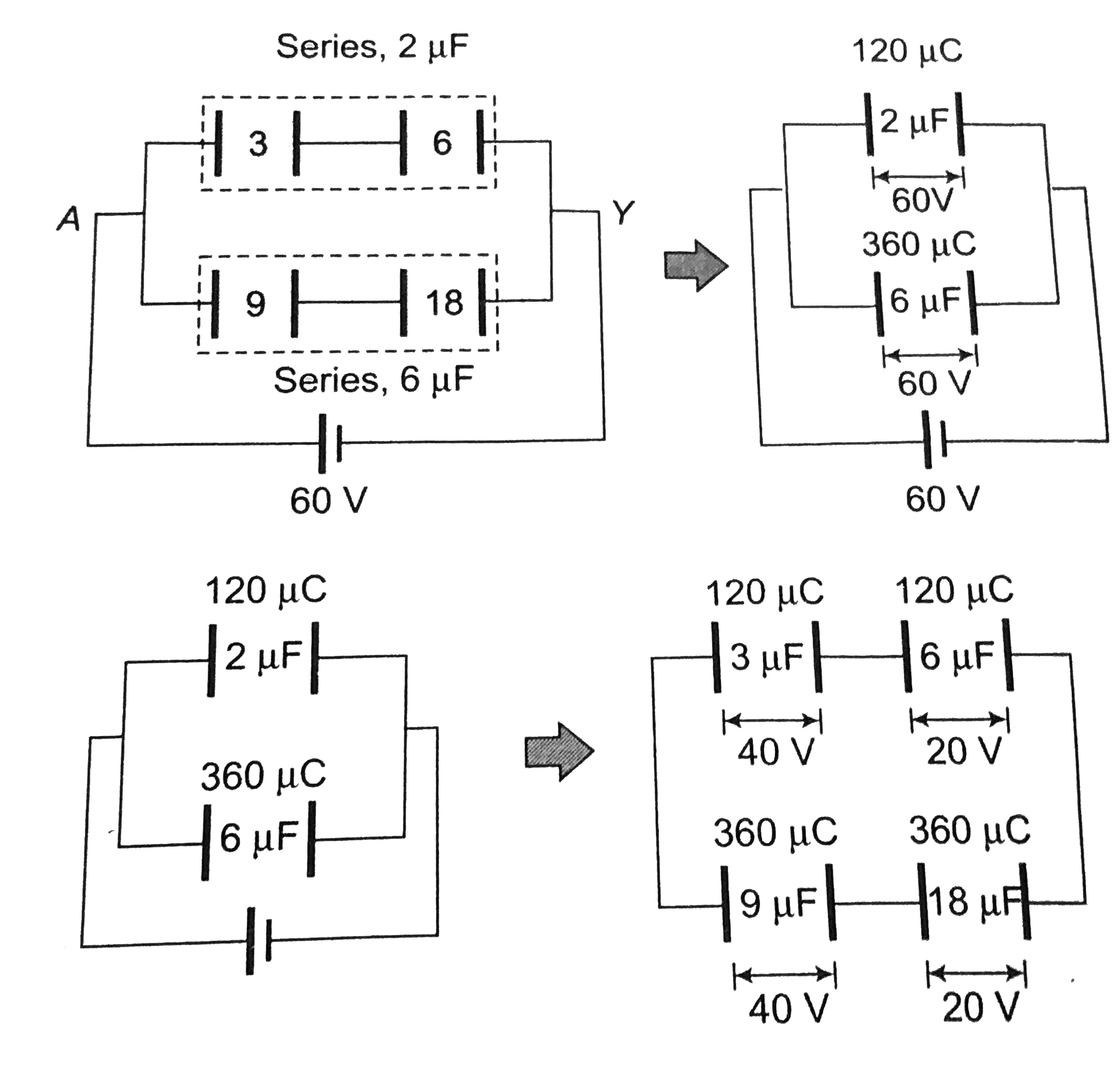
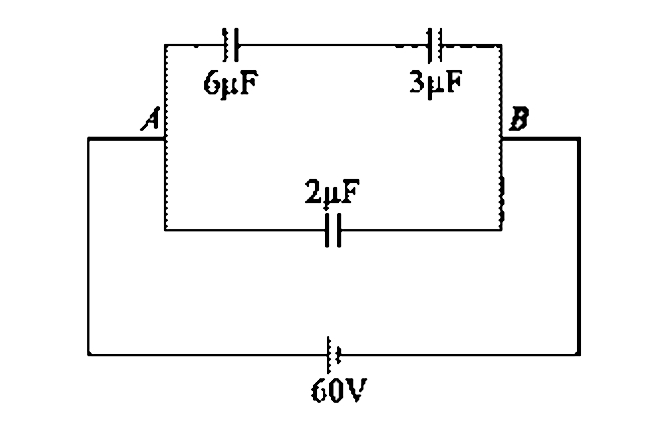
Here, two branches are in parallel. Potential difference across each branch Is 60V. There are two capacitors in series, use direct formulae as explained earlier.
V1=(63+6)×60=40V,V2=60−V1=20V
V3=(189+18)×60=40V,V4=60−V3=20V
charge on
3μF:3×40=120μC
6μF:6×20=120μC
9μF:9×40=360μC
18μF:18×20=360μC
Alternative Method :
Topper's Solved these Questions
Similar Questions
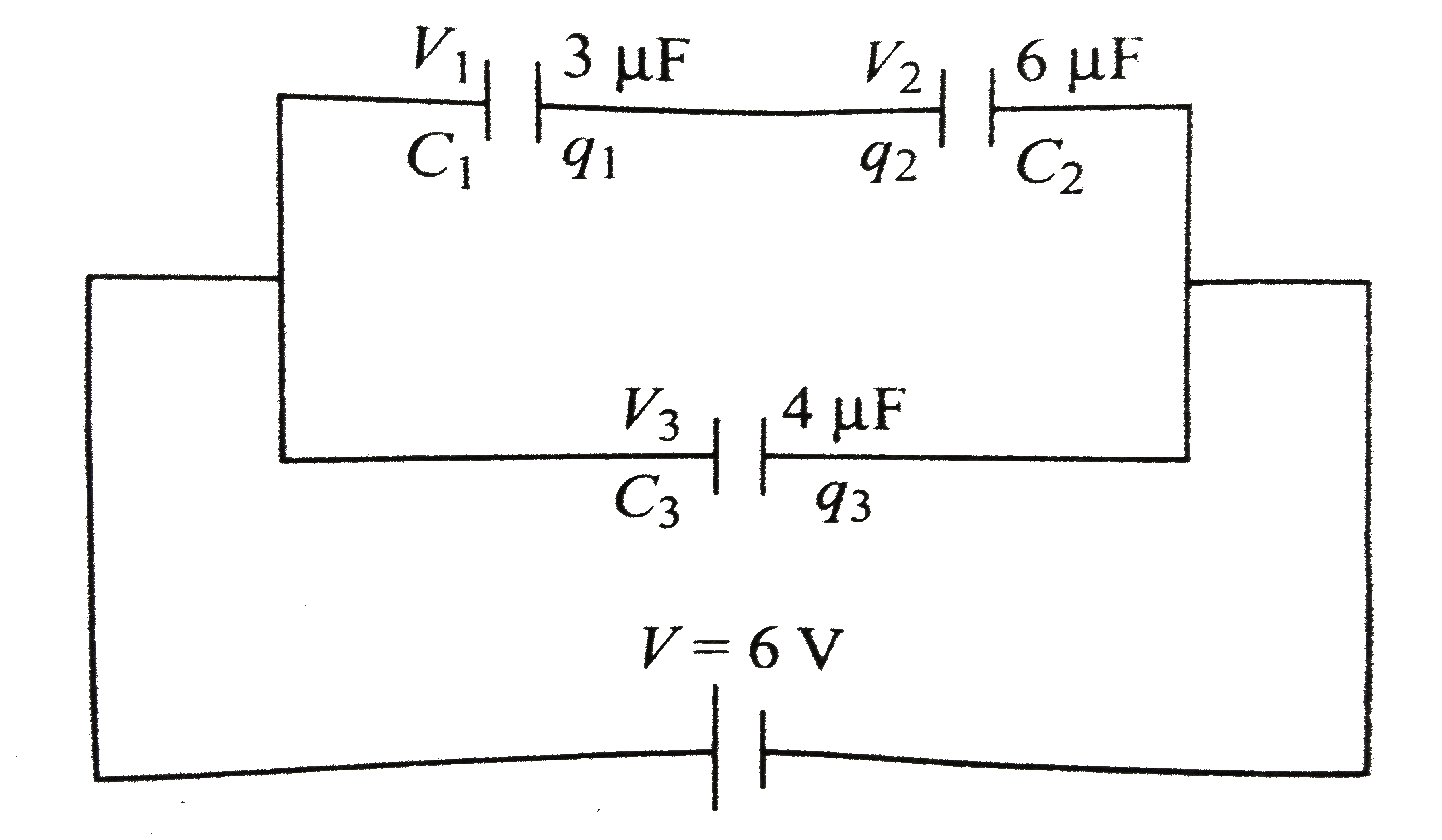
Three capacitors of capacitances 3μF, 6μF, and 4μF are connected as shown across a battery of emg6V.
 .
.
i. Find the equivalent capacitance,
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in the system of capacitors and total energy stored in the system of capacitor.
View SolutionThree capcitors of capacitances 4μF,
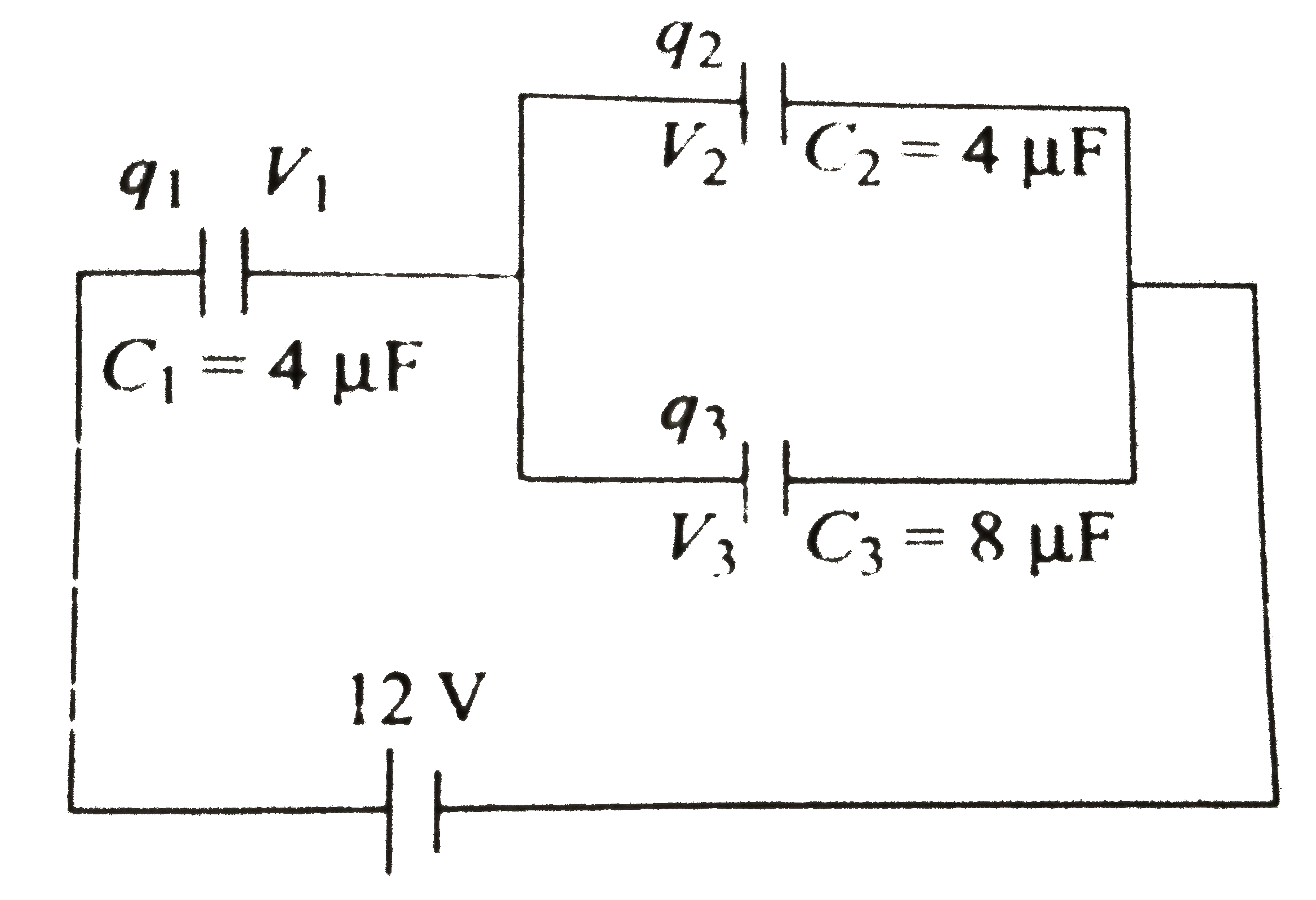 .
.
4μF, and 8μF, are connected as show across a battery of emf 12V.
i. Find the equivalent capacitane.
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in each capacitor and the total energy stored in the system of capacitors.
View Solution
Knowledge Check
Find equivalent capacitance across AB (all capacitances in μF)
 A203μFB9μFC48μFDNone
A203μFB9μFC48μFDNonePotential difference of 11 V is applied across three capacitors of capacitance 1μF,2μFand3μF connected in series. Potential difference across capacitor of 1μF is:
A4 VB6 VC1 VD2 VIn the circuit shown, the potential difference across the 3μF capacitor is V and the equivalent capacitance between A and B is C Then:
 AC=4μFBC=11μFCV=20VDV=40V
AC=4μFBC=11μFCV=20VDV=40V
Find charge and potential on each capacitor. All capactances are in μF.
View SolutionA capacitor of capacitance 5 μF is charged to a potential difference of 10 volts and another capacitor of capacitance 9 μF is charged to a potential difference of 8 volts. Now these two capacitors are connected in such a manner that the positive plate of one is connected to the positive plate of other. Calculate the common potential difference across the two capacitors.
View SolutionTwo capacitors of capacitances C1=6μFandC2=3μFare connected in series across a cell of emf 18 V. Calculate
(i) the equivalent capacitance,
(ii) the potential difference across each capacitor,
(iii) the charge on each capacitor.
View SolutionA 10μF capacitor is charged to a potential difference of 50V and is connected to another uncharged capacitor in parallel. Now the common potential difference becomes 20 volt. The capacitance of second capacitor is
View SolutionIn the follwong diagram the charge and potential difference across 8μF. Will capacitance will be respectively

View Solution

