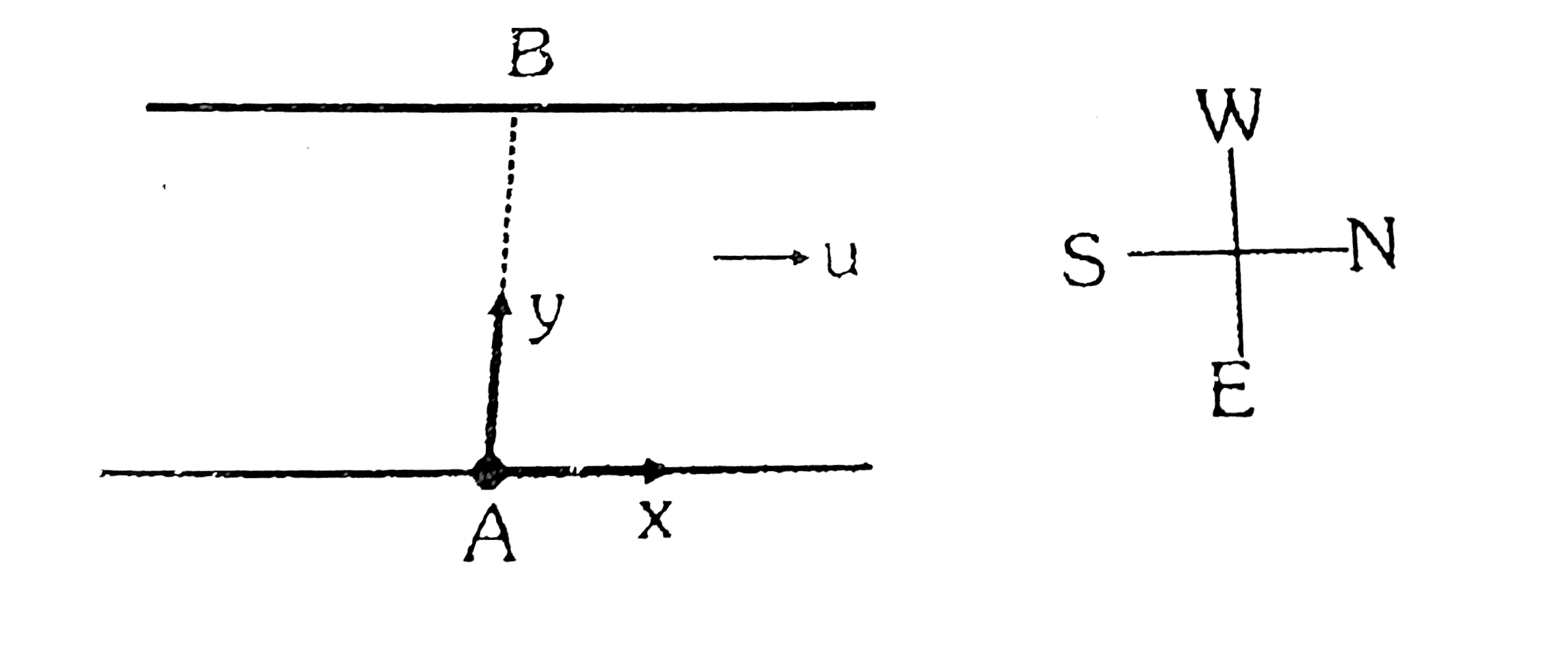
A river of width a with straight parallel banks flows due north with speed u. The points O and A are on opposite banks and A is due east of O. Coordinate axes and are taken in the east and north directions respectively. A boat, whose speed is v relative to water, starts from O and crosses the river. If the boat is steered due east and u varies with Find
(a) equation of trajectory of the boat,
(b) time taken to cross the river,
(c) absolute velocity of boatman when he reaches the opposite bank,
(d) the displacement of boatman when he reaches the opposite bank from the initial position.
The correct Answer is:B
Let be the velocity of boatman relative to river, the velocity of river and is the absolute velocity of boatman.Then
Given , and
Now
and
Dividing (1) by (2), we get
or
or or
This is the desired equation of trajectory.

Topper's Solved these Questions
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Integer
Explore 6 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-Vi single answer
Explore 30 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level -V Multi answer
Explore 18 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
Similar Questions
A river of width 'd' with straight parallel banks flows due North with speed u. A boat, whose speed is v relative to water, starts from A and crosses the river. If the boat is steered due West and u varies with y as u=y(d−y)vd2 then answer the following questions.
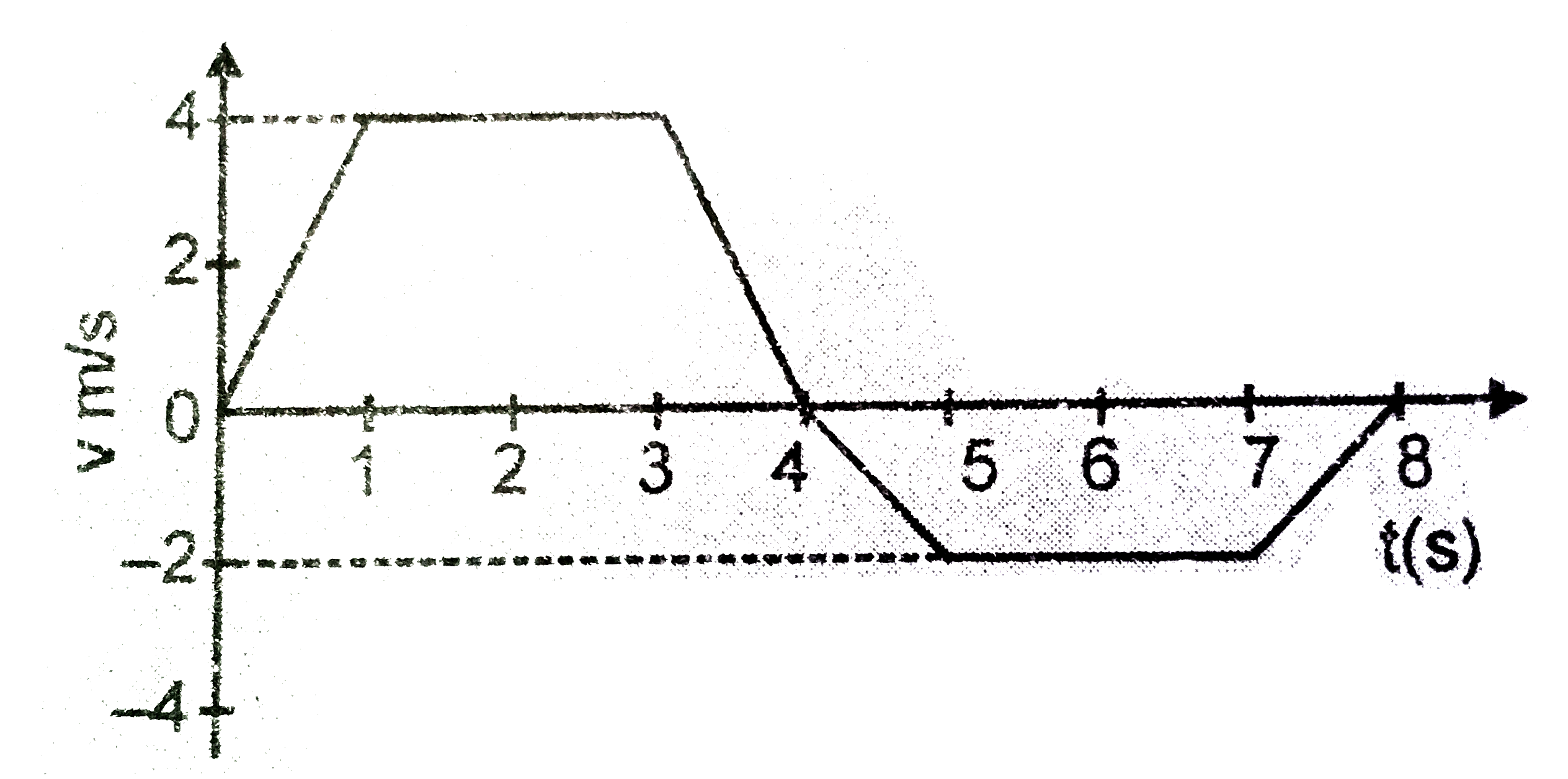
The time take by boat to cross the river is
View SolutionVelocity of the boat with respect to river is 10m/s. From point A it is steered in the direction shown. Where will it reach on the opposite bank ?

View Solution
Knowledge Check
A river of width 'd' with straight parallel banks flows due North with speed u. A boat, whose speed is v relative to water, starts from A and crosses the river. If the boat is steered due West and u varies with y as u=y(d−y)vd2 then answer the following questions.
Absolute velocity of boat when it reaches the opposite bank isA43v, towards EastBv, towards WestC43v, towards WestD→v, towards EastA river of width 'd' with straight parallel banks flows due North with speed u. A boat, whose speed is v relative to water, starts from A and crosses the river. If the boat is steered due West and u varies with y as u=y(d−y)vd2 then answer the following questions.

Equation of trajectory of the boat isAy=x22dBx=y22dCy=x22d−x33d2Dx=y22d−y33d2A man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
AThe minimum time in which he can cross the river is bvBHe can reach a point exactly opposite on the bank in time t=b√v2−u2ifv>uCHe cannot reach a point exactly opposite on the bank if u>vDHe cannot reach a point exactly opposite on the bank if v>u
A river flows due south with a speed of 2.0ms−1. A man strees a motorboat across the river , his velocity relative to the water is 4ms−1 due east. The river is 800m wide.
(a) What is his velocity (magnitude and direction) relative to the earth ?
(b) How much time is required to cross the river ?
( c) HOw far south of his starting points will he reach the opposite bank ?
View SolutionA man goes 10m due east and then 24 m due north. Find the distance from the starting point.
View SolutionA man who can swim at a speed v relative to the water wants to cross a river of width d, flowing with a speed u. The point opposite him across the river is P.
View SolutionA man who can swim at a speed v relative to the water wants to cross a river of width d flowing with a speed u. The point opposite him across the river is A.
View SolutionA man can swim in still water at a speed of 6kmph and he has to cross the river and reach just opposite point on the other bank.If the river is flowing at a speed of 3kmph,and the width of the river is 2km, the time taken to cross the river is (in hours)
View Solution