A particle slides down a frictionless paraboli (y=x2) track (A−B−C) starting from rest at point A.Point B is at the vertex of parabola and point C is at a height less than that of point A.After C,the particle moves freely in air as a projectile. If the particle reaches highest point at P,then
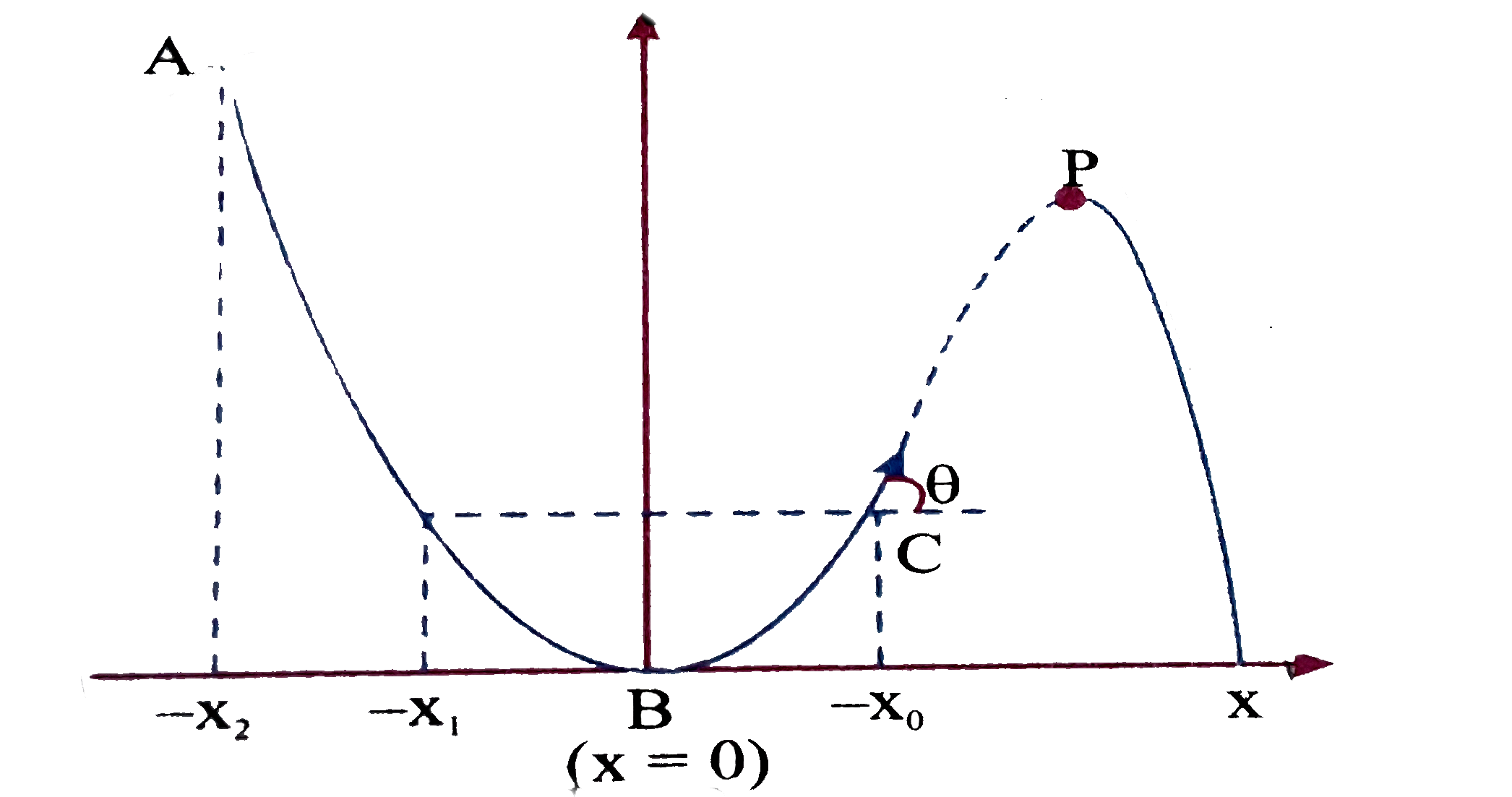
KE at P=KE at B
height at P=height at A
total energy at P=total energy at A
time of travel from A to B =time of travel from B to P
The correct Answer is:C
In this type of question, nature of track is very important of consider, as friction is not in this track, total energy of the particle will remain constant throughtout the journey.
(KE)B>(KE)P
(PE)P<(PE)A
As, heightofp<HeightofA
Hence, path≤n>hAB>path≤n>hBP
Hence,time of travel from A "to" B ne Time of travel from B "to" P.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - NCERT BASED QUES. PASSAGE8videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level -V Single answer31videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - NCERT BASED QUES. SINGLE ANS.8videos
MOTION IN A PLANE
- BOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)24videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W29videos
MOTION IN A STRAIGHT LINE
Similar Questions
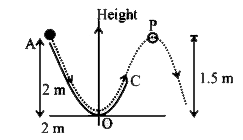
A particle (m = 3 kg) slides down a frictionless track (AOC) starting from rest at a point A (height 2m). After reaching C, the particle continues to move freely in air as a projectile. When it reaching its highest point P (height 1.5 m) the kinetic energy of the prarticle (in J) is : Figure drawn is schematic and not to scale , take g = 10ms−2
 View Solution
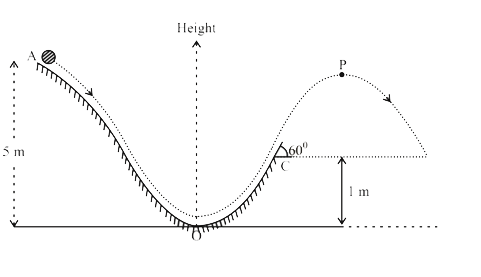
View SolutionA particle (m = 2 kg) slides down a smooth track AOC starting from rest at point A (height = 5m). After reaching point C (height =1m), the particle continues to move freely in air as a projectile. The particle velocity at point C is at angle 60∘ with the horizontal. The maximum height attained by particle after leaving point C is _____(in m). [figure drawn is schematic and hot to scale : take =ms−2]
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m slides on a frictionaless surface ABCD, starting from rest as shown in figure. The part BCD is a circular arc. If it looses contact at point P, the maximum height attained by the particle from point C is
 A(a) R[2+12√2]B(b) R[1+12√2]RC(c) 3RD(d) None of these
A(a) R[2+12√2]B(b) R[1+12√2]RC(c) 3RD(d) None of these - Question 2 - Select One
Velocity of a particle varies with time as v=atˆi+2ht2ˆj. If the particle starts from point (0,c), the trajectory of the particle is
Ay=bx3/2a+cBy=4√2b3(xa)3/2+cCy=4√2b3(xa)3/2−cDy=bx3/2a−c - Question 3 - Select One
A particle starts from point A moves along a straight line path with an acceleration given by a=p−qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
ApqBp√qCqpD√qp
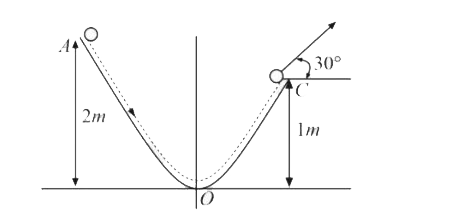
A particle (m = 1kg) slides down a frictionless track (AOC) starting from rest at a point A (height 2m). After reaching C, the particle continues to move freely in air as a projectile. When it reaches point C (height 1 m), the vertical speed of the particle (in m/s) is (Figure drawn is schematic and not to scale , take g = 9.8 m/sec2) [Take ]
 View Solution
View SolutionIn the illustration 1 if the particle shifts from Points P to points C find the displacement of the particle.
View Solution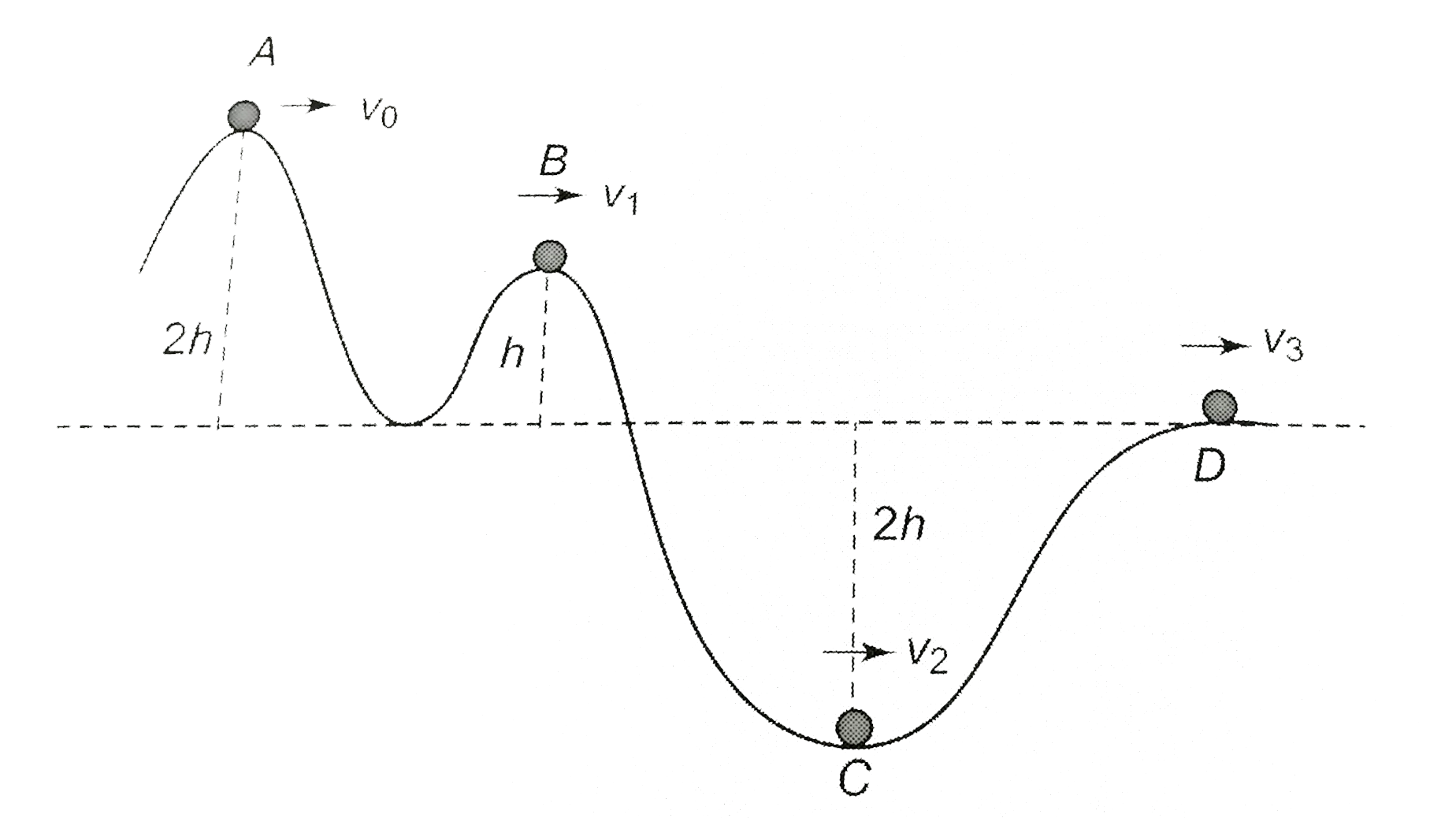
A particle is given velocity v0 at point A as shown in the figure. Find the speed of particle at point B,C and DView SolutionNormal to the parabola y2=8x at the point P (2, 4) meets the parabola again at the point Q. If C is the centre of the circle described on PQ as diameter then the coordinates of the image of point C in the line y=x are
View SolutionA particle moves on a path as shown. The particle takes 10 seconds in going from starting point to the final point. What is the average velocity vector of the particle ?
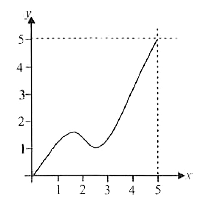 View Solution
View Solution

