Question

Reciprocal squared function and properties

Explanation

What is Reciprocal squared function and properties?

Did you know that the swinging motion of the pendulum can be modeled using mathematical properties and equations? For instance, the frequency (in Hertz), which is the number of full swings per second of one swing of the pendulum, is equal to the reciprocal of the period (in seconds), which is the time it takes for the pendulum to make one full swing back and forth.

Recall that the reciprocal of a number x is 1/x, so, we can find the frequency of a pendulum's swinging motion by finding the reciprocal of the period. For instance, consider a pendulum with a period of 2 seconds. To find the frequency of this pendulum, we find the reciprocal of 2, which is 1/2.

Pretty neat, huh? Let's take it a step further. In general, if we let the frequency of a pendulum be f and the period of a pendulum be p, we have that f = 1/p. In mathematics, we call this a reciprocal function. In the same way that the reciprocal of a number x is 1/x, the reciprocal function of a function f(x) is 1/f(x).

For example, let us consider the function f(x) = 2x - 1. The reciprocal function of f would be as follows:

1/f(x) = 1/(2x - 1)

So far so good! In general, a reciprocal function has the form:

r(x) = a / (x - h) + k

Being familiar with a reciprocal function in this form better allows us to identify various characteristics of the function. Let's consider some of those characteristics.

Reciprocal Function Characteristics

In observing the characteristics of reciprocal functions, we will consider the most basic reciprocal function, which is f(x) = 1/x. Take a look at the graph of this function.

  

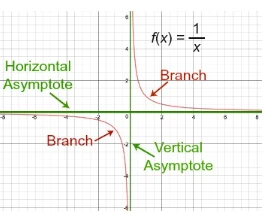
Notice that our graph has two main parts. We call these the branches of the function. Also notice that the function's graph approaches the lines x = 0 and y = 0, but it never actually touches them. We call these lines the asymptotes, which are the horizontal and vertical lines that the graph approaches but doesn't touch. The asymptotes come from the fact that a reciprocal function 1/f(x) must restrict its domain so that the denominator is not equal to 0.

If we're given a reciprocal function in the form 1/f(x), then we can find the vertical asymptotes by setting f(x) = 0 and solving for x. However, when given a reciprocal function in its general form, it's much easier. For the reciprocal function in general form r(x) = a / (x - h) + k, we have the following rules:

1. The vertical asymptote of r(x) is x = h.


2. The horizontal asymptote of r(x) is y = k.

Well, that's fairly simple! It's just a matter of identifying numbers within the function! The only thing to keep in mind is that the denominator in the general form is x - h, so when identifying the vertical asymptote, x = h, we must keep that negative in mind.

We can use these asymptotes, a few plotted points, and the general shape of the graph to sketch a graph of a reciprocal function. So, being able to identify the asymptotes easily is definitely helpful.