Modulus function and properties
What is Modulus function and properties?
Modulus Function is defined as the real valued function f:R→R , y = |x| for each x∈R
When it comes to the non-negative value of x, f(x) is equal to x. In case of negative values of x, the value of f(x) is the negative of the value of x
f(x)=|x|={x if x≥0−x if x<0f(x)=|x|={x if x≥0−x if x<0
It is also called the absolute value function

Example
|-3| =3
|-2|=2
|2|=2
We know that all the real number can be plotted on the real number line. The absolute value function is used to measure the distance between two numbers on the number line.. Thus, the distance between x and 0 is |x - 0| = |x|. So |x| represent the distance of the number from the origin. Similarly the distance between x and y is |x - y|. Thus, the distance from -3 to -1 is |-3 - (-1)| = |-3 + 1| = |2| = 2, and the distance from -3 to 5 is |-3 - 5| = |-8| = 8
Domain and Range of the Modulus Function(absolute value function)
For f:R→R,y=f(x)=|x| for each x∈R
Domain = R
Range = R+=x∈R:x≥0
Graph of the Modulus Function
The graph of the modulus function is shown below. It coincide with the graph of Identity Function y = x for x≥0 and for x< 0, it is a graph of Linear Function y=−x
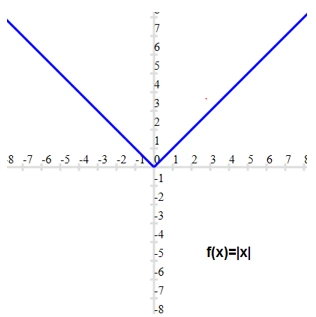
Here at x=0 ,the graph is turning upward. So x=0 is the turning point in this graph
Properties of the Modulus Function
The modulus function has the following properties
1. For any real number x , we have
√x2=|x
2. ||x||= |x|
3. if a and b are positive real numbers
a. x2≤a2⇔|x|≤a⇔−a≤x≤a
b. x2≥a2⇔|x|≥a⇔x≤−aorx≥a
c. x22⇔|x|⇔−a
d. x2>a2⇔|x|>a⇔x<−aorx>a
e. a2≤x2≤b2⇔a≤|x|≤b⇔x∈[−b,−a]∪[a,b]
f. a22⇔a<|x|⇔x∈(−b,−a)∪(a,b)
4. if a is negative
a. |x| geq a , x in Rb.|x|≤a,x=ϕ
5. 3. For real number x and y
a. |xy|=|x||y|
b. |xy|=|x||y|,y≠0|
c. |x+y|≤|x|+|y|
|x−y|≤|x|+|y|
for x,y≥0orx,y<0,|x+y|=|x|+|y|
d. |x+y|≥|x|−|y||x+y|
|x−y|≥|x|−|y|
for x,y≥0and|x|≥|y|yorx, y<0and|x|≥|y|,|x−y|=|x|−|y|
Solved examples of Modulus Functions (absolute value function)
1. Find the domain and range of the below function?
a. y=|1−x|
b. y=2−|1−x|y
c. y=2√x−|x|
Solution
a. y=|1−x|
Clearly This is defined for x∈R. So Domain is R
Now |1−x|≥0 for all x∈R
So Range is [0,∞)
b. y=2−|1−x|
Clearly This is defined for x∈R. So Domain is R
Now |1−x|≥0for all x∈R
or
−|1−x|≤0
2−|1−x|≤22 for all x∈R
So Range is (−∞,2]
c. y=2√x−|x|
Now
x−|x|={x−x=0 if x≥0x+x=2x if x≤0
Therefore, 2√x−|x| is undefined for all x∈R
So domain of the function is ϕ
2. Draw the graph of the below function?
a. y=x + |x|
b. y = x -|x|
c. y =|x-1|
Solution
We need to convert this function into simple form before drawing the graph
a. y=x + |x|
This can be written as
y=x+|x|={x+x=2x if x≥0x−x=0 if x<0y
So, This is a linear function y =2x for x≥0 and linear function y =0 for x<0
So graph will be
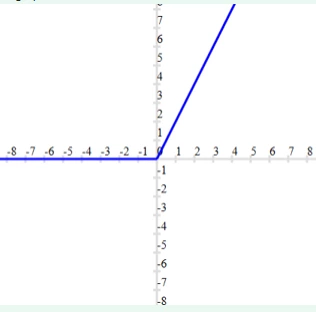
b.y = x -|x|
This can be written as
y=x−|x|={x−x=0 if x≥0x+x=2x if x<0y=x−|x|={x−x=0 if x≥0
So, This is a Linear Function y =0 for x≥0 and linear function y =2x for x<0
So graph will be
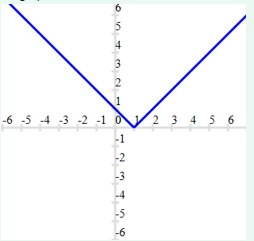
Important thing to note here is that the turning point of the graph is x=1 here.
When it comes to the non-negative value of x, f(x) is equal to x. In case of negative values of x, the value of f(x) is the negative of the value of x
f(x)=|x|={x if x≥0−x if x<0f(x)=|x|={x if x≥0−x if x<0

|-3| =3
|-2|=2
|2|=2
We know that all the real number can be plotted on the real number line. The absolute value function is used to measure the distance between two numbers on the number line.. Thus, the distance between x and 0 is |x - 0| = |x|. So |x| represent the distance of the number from the origin. Similarly the distance between x and y is |x - y|. Thus, the distance from -3 to -1 is |-3 - (-1)| = |-3 + 1| = |2| = 2, and the distance from -3 to 5 is |-3 - 5| = |-8| = 8
For f:R→R,y=f(x)=|x| for each x∈R
Range = R+=x∈R:x≥0
The graph of the modulus function is shown below. It coincide with the graph of Identity Function y = x for x≥0 and for x< 0, it is a graph of Linear Function y=−x

1. For any real number x , we have
√x2=|x
2. ||x||= |x|
a. x2≤a2⇔|x|≤a⇔−a≤x≤a
b. x2≥a2⇔|x|≥a⇔x≤−aorx≥a
c. x22⇔|x|⇔−a
d. x2>a2⇔|x|>a⇔x<−aorx>a
e. a2≤x2≤b2⇔a≤|x|≤b⇔x∈[−b,−a]∪[a,b]
f. a22⇔a<|x|⇔x∈(−b,−a)∪(a,b)
a. |x| geq a , x in Rb.|x|≤a,x=ϕ
a. |xy|=|x||y|
a. y=|1−x|
b. y=2−|1−x|y
c. y=2√x−|x|
Solution
a. y=|1−x|
Clearly This is defined for x∈R. So Domain is R
Now |1−x|≥0 for all x∈R
So Range is [0,∞)
b. y=2−|1−x|
Clearly This is defined for x∈R. So Domain is R
Now |1−x|≥0for all x∈R
or
−|1−x|≤0
2−|1−x|≤22 for all x∈R
So Range is (−∞,2]
c. y=2√x−|x|
Now
x−|x|={x−x=0 if x≥0x+x=2x if x≤0
Therefore, 2√x−|x| is undefined for all x∈R
So domain of the function is ϕ
2. Draw the graph of the below function?
a. y=x + |x|
b. y = x -|x|
c. y =|x-1|
Solution
We need to convert this function into simple form before drawing the graph
a. y=x + |x|
This can be written as
y=x+|x|={x+x=2x if x≥0x−x=0 if x<0y
So, This is a linear function y =2x for x≥0 and linear function y =0 for x<0
So graph will be

This can be written as
y=x−|x|={x−x=0 if x≥0x+x=2x if x<0y=x−|x|={x−x=0 if x≥0
So, This is a Linear Function y =0 for x≥0 and linear function y =2x for x<0
So graph will be

Similar Questions
Laws OF exponent OF nth root OF number|| Radical||Interval||Inequality|| Modulus function properties OF modulus function
View SolutionReciprocal squared function and properties
View SolutionFractional part function and properties
View SolutionGreatest integer function and properties
View SolutionSmallest integer function and properties
View SolutionLogarithmic function and properties
View SolutionProperty 1 (Modulus function) For any real no. x √x2=|x|
View SolutionProperty 2(i) (Modulus function) If a and b are positive real no's then (1)x2≤a2(2)x2≥a2(3)x2<a2(4)x2>a2
View SolutionModulus and Locus | Properties of Modulus And Locus Questions
View SolutionModulus function / Absolute function || Modulus inequality and illustration
View Solution

