A starts from rest and moves with acceleration a1. Two seconds later B starts from rest and moves with an acceleration a2. If the displacement of A in the 5th second is the same as that of B in the same interval, the ratio of a1 to a2 is
9:5
5:9
1:1
1:3
The correct Answer is:B
To solve the problem, we need to find the ratio of the accelerations a1 and a2 of two bodies A and B, given that their displacements in specific time intervals are equal. Let's break it down step by step.
Step 1: Understand the Motion of A
- Body A starts from rest with an acceleration a1.
- The displacement of A in the nth second can be calculated using the formula:
Sn=u+a2(2n−1)
where u is the initial velocity, a is the acceleration, and n is the second.
- Since A starts from rest, u=0. Thus, the displacement of A in the 5th second (SA) is:
SA=0+a12(2⋅5−1)=a12⋅9=9a12
Step 2: Understand the Motion of B
- Body B starts from rest with an acceleration a2 but starts 2 seconds later than A.
- Therefore, when A has traveled for 5 seconds, B has traveled for 5−2=3 seconds.
- The displacement of B in the 3rd second (SB) is given by the same formula:
SB=0+a22(2⋅3−1)=a22⋅5=5a22
Step 3: Set the Displacements Equal
- According to the problem, the displacement of A in the 5th second is equal to the displacement of B in the 3rd second:
SA=SB
9a12=5a22
Step 4: Simplify the Equation
- We can eliminate the 12 from both sides:
9a1=5a2
Step 5: Find the Ratio of Accelerations
- Rearranging the equation gives us:
a1a2=59
Conclusion
- The ratio of the accelerations a1 to a2 is:
a1a2=59
- Body A starts from rest with an acceleration a1.
- The displacement of A in the nth second can be calculated using the formula:
Sn=u+a2(2n−1)
where u is the initial velocity, a is the acceleration, and n is the second.
SA=0+a12(2⋅5−1)=a12⋅9=9a12
- Body B starts from rest with an acceleration a2 but starts 2 seconds later than A.
- Therefore, when A has traveled for 5 seconds, B has traveled for 5−2=3 seconds.
SB=0+a22(2⋅3−1)=a22⋅5=5a22
- According to the problem, the displacement of A in the 5th second is equal to the displacement of B in the 3rd second:
SA=SB
9a12=5a22
- We can eliminate the 12 from both sides:
9a1=5a2
- Rearranging the equation gives us:
a1a2=59
- The ratio of the accelerations a1 to a2 is:
a1a2=59
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 3 C.W
Explore 25 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Single Type Question
Explore 23 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 1 C.W
Explore 20 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-II(H.W)
Explore 31 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
Similar Questions
An object A starts from rest and moves with acceleration a_(1).Two seconds later,another object 'B' starts from rest and moves with an acceleration a_(2) .If the displacement of A in the 5th second is the same as that of B in the same interval,the ratio of a_(1) to a_(2)is
View Solution5.A body A starts from rest with an acceleration "a_(1)".After two seconds,another body B starts from rest with an acceleration "a_(2)".If they travel equal distances in the "5" th second after the start of "A",then the ratio of "a_(1):a_(2)" is equal to 1) "5:9," 2) "9:5," 3) "5:7," 4) "7:5"
View Solution
Knowledge Check
A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
A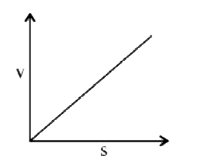 B
B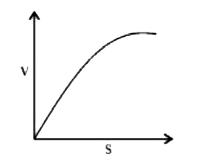 C
C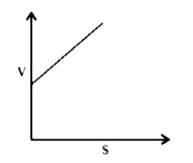 D
D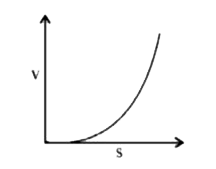
A body P starts from rest with an acceleration a1. After 2 seconds, another body Q starts from rest with an acceleration a2 from the same point. If they travel equal distances in the fifth second after starting of the motion of the P, then the ratio a1:a2 is equal to
A5:9B5:7C9:5D9:7A body A starts from rest with an acceleration a1. After 2 seconds, another body B starts from rest with an acceleration a2. If they travel equal distances in the 5th second, after the start of A, then the ratio a1:a2 is equal to :
A5:9B5:7C9:5D9:7
A body A starts from rest with an acceleration a1. After 2 seconds, another body B starts from rest with an acceleration a2. If they travel equal distances in the 5th second, after the start of A, then the ratio a1:a2 is equal to :
View SolutionA bus starts from rest and moves whith acceleration a=2ms2. The ratio of the distance covered in 6th second to that covered in 6 seconds is
View SolutionA body starts from rest and moves with constant acceleration. The ratio of distance covered by the body in nth second to that covered in n second is.
View SolutionA body starting from rest and has uniform acceleration
8m/s2 . The distance travelled by it in5th second will be
View SolutionA body starting from rest is moving with a uniform acceleration of 8ms2. Then the distance travelled by it in 5th second will be
View Solution
