A luminous object O is located at the bottom of a big pool of liquid of refractive index μ and depth h. The object O emits rays upwards in all directions, so that a circle of light is formed at the surface of the liquid by the rays which are refracted into the air. what happens to the rays beyond the circle ? Determine the radius and the area of the circle .
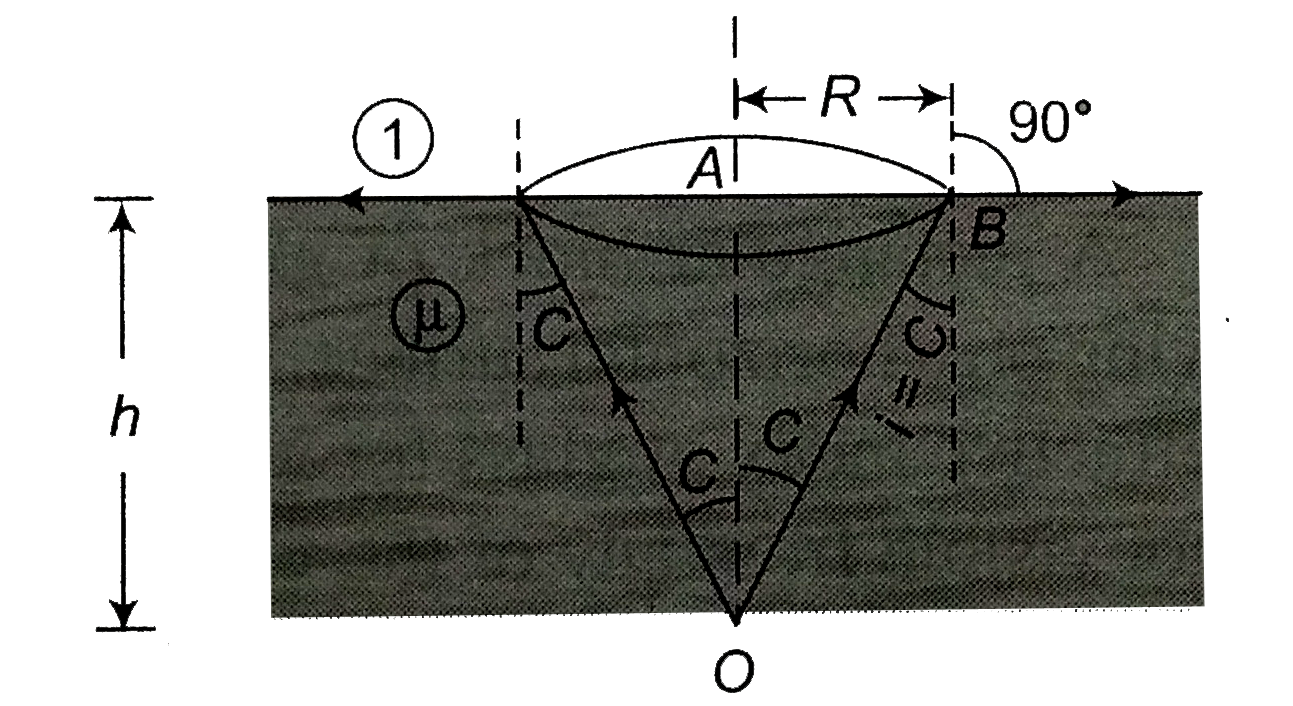
μsinC=1×sin90∘
sinC=1/μ
When i<C, rays are refracted into air
When i=C, r=90∘
i>C, T.I.R. takes place
ΔOAB,
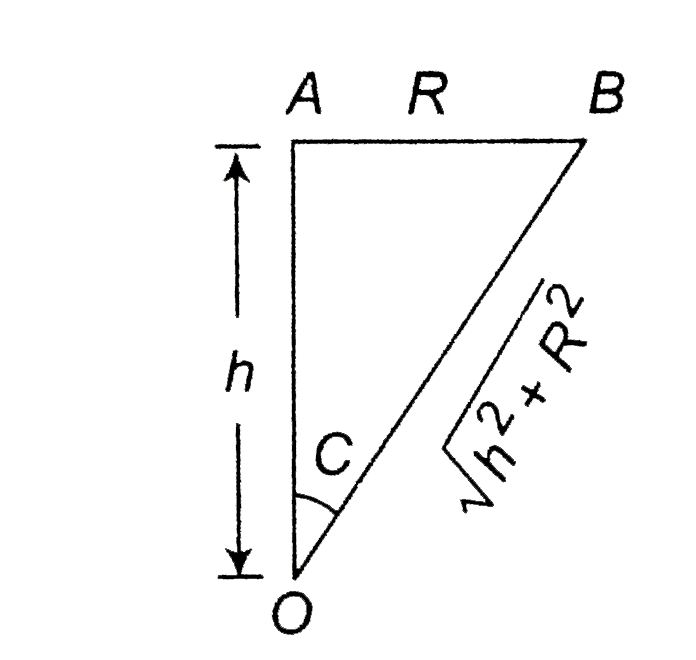
sinC=R√h2+R2
1μ=R√h2+R2
1μ2=R2h2+R2⇒h2+R2=μ2R
(μ2−1)R2=h2
R=h√μ2−1
Topper's Solved these Questions
- REFRACTION OF LIGHT BY PLANE SURFACESBOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises
110 Videos
- REFRACTION AT SPHERICAL SURFACESBOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES
105 Videos
- SEMICONDUCTORSBOOK - CP SINGHCHAPTER - SEMICONDUCTORSEXERCISE - Exercises
140 Videos
Similar Questions
An object is placed at the bottom of a tank filled with liquid of refractive index 1.6. If the actual depth of the tank is 10 cm, what will be the apparent depth of the object?
View SolutionGive three examples of materials that refract light rays. What happens to the speed of light rays when they enter these materials?
View Solution
Knowledge Check
When a ray of light is incident normally on one refracting surface of an equilateral prism of refractive index 1.5, then
Athe ray undergoes total internal reflection at the second refracting surface of prismBemergent ray is deviated by 30∘Cemergent ray is deviated by 60∘Demergent ray just grazes the second refracting surface of the prismA concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
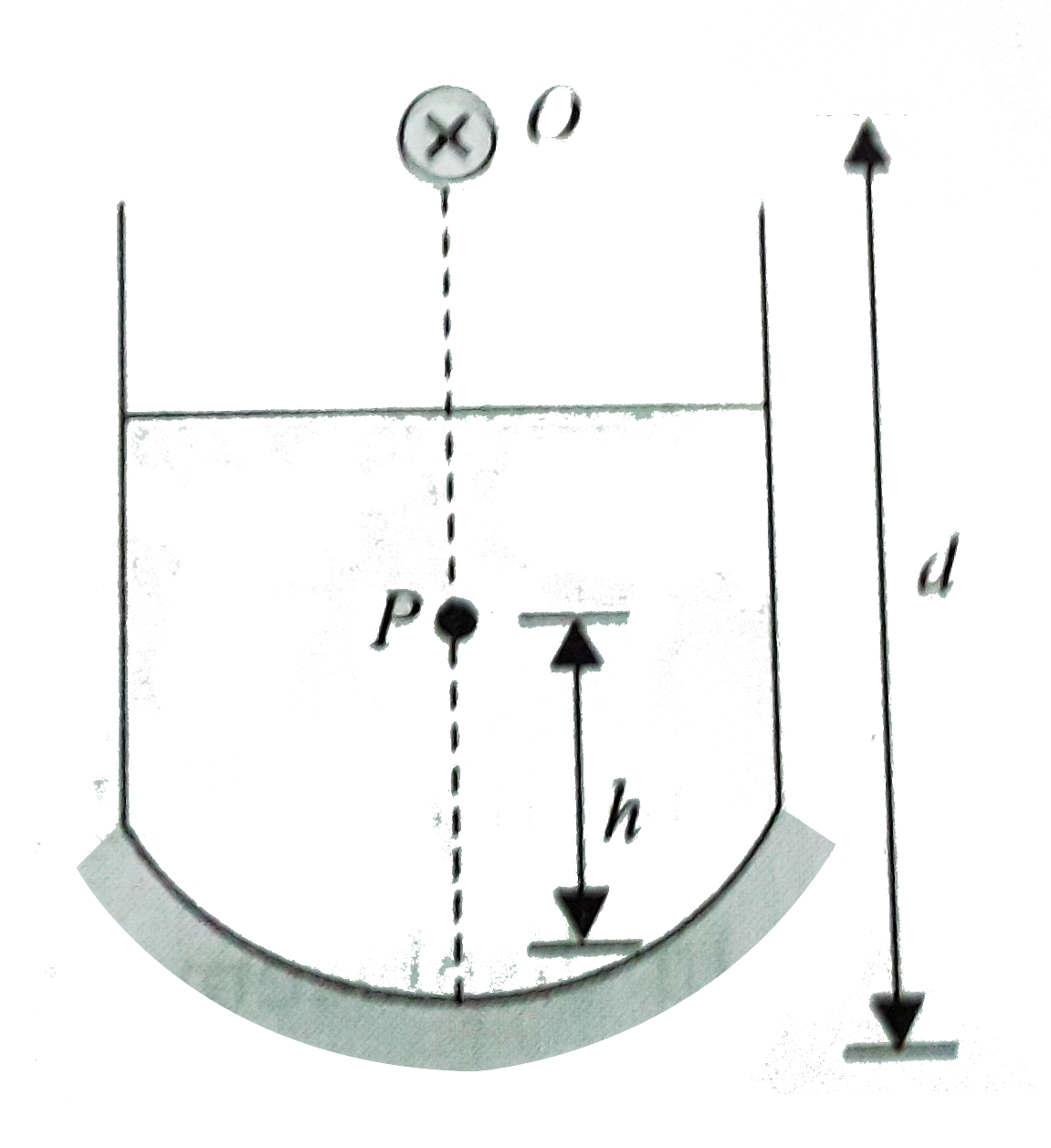 Ah(1−1μ)B2hμ−1CzeroD2hμ
Ah(1−1μ)B2hμ−1CzeroD2hμA ray of light is incident on the surface of plate of glass of refractive index 1.5 at the polarising angle. The angle of refraction of the ray will be
A33.7∘B23.7∘C43.7∘D53.7∘
The apparent depth of an object at the bottom of tank filled with a liquid of refractive index 1.3 is 7.7 cm. what is the actual depth of the liquid in the tank ?
View SolutionA metal coin at the bottom of a beaker filled with a liquid of refractive index 4/3 to height of 6cm. To an observer looking from above the surface of the liquid, coin will appear at a depth of (consider paraxial rays).
View SolutionA ray of light is incident on a medium at an angle i. It is found that the reflected ray is at right angles to the refracted ray . The refractive index of the medium is given by
View SolutionA water drop in air refractes the light ray as
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5
View Solution
