A mass m = 50 g is dropped on a vertical spring of spring constant 500 N nfl from a height h= 10 cm as shown in figure (18-E14). The mass sticks to the spring and executes simple harmonic oscillations after that. A concave mirror of focal length 12 cm facing the mass is fixed with its principasl axis coinciding with the lilne of motion of the mss, its pole being at a distance of 30 cm from the free end of the spring. Find the length in which the image of the mass oscillates


x: maximum compression of spring
Applying energy conservation (1) and (2)
mg(h+x)=12kx2
501000x10(0.1+x)=12×500x2
500x2−x−0.1=0
x=1±√1+4×500×0.12×500=0.015m=1.5cm
The block is in equilibrium when mg=kx0
501000×10=500x0⇒x0=10−3m=0.1cm
Amplitude of oscillation =x−x0=1.5−0.1=1.4cm
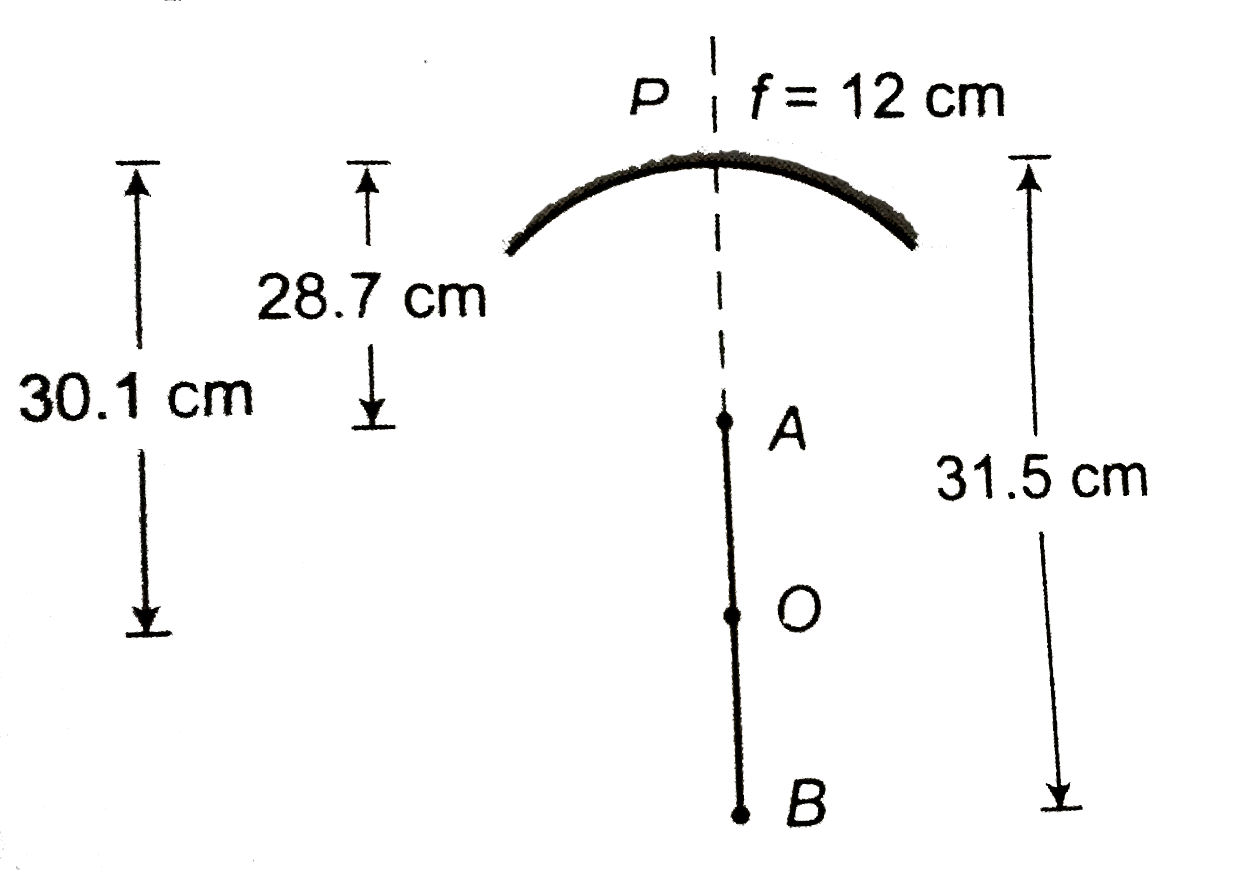
O: equilibrium position PO=30.1cm,PB=31.5cm
image of A:
1vA+1−28.7=1−12
vA=−20.6cm
Image of B:
1vB+1−31.5=1−12
vB=−19.4cm
The length in which image oscillates
=20.6−19.4=1.2cm
Topper's Solved these Questions
- REFLECTION OF LIGHTBOOK - CP SINGHCHAPTER - REFLECTION OF LIGHTEXERCISE - EXERCISES
67 Videos
- PHOTOELECTRIC EFFECTBOOK - CP SINGHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - EXERCISES
73 Videos
- REFRACTION AT SPHERICAL SURFACESBOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES
105 Videos
Similar Questions
A mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
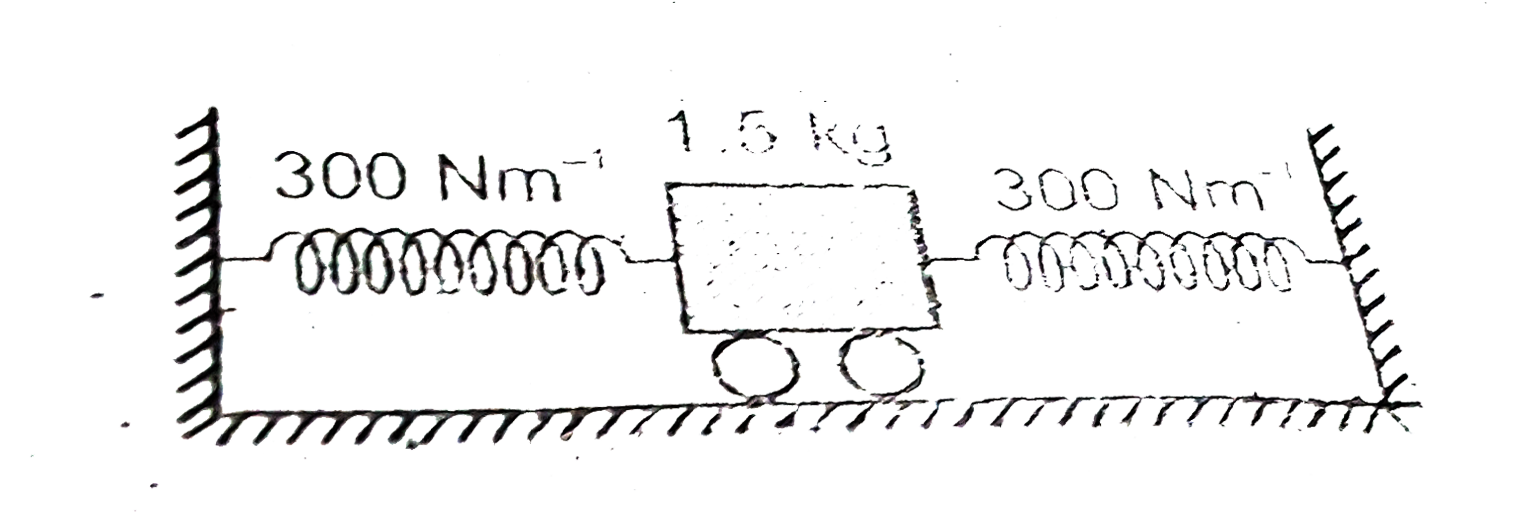
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
Knowledge Check
A block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
A20Nm−1B40Nm−1C30Nm−1D60Nm−1A body of mass 1 kg suspended by a light vertical spring of spring constant 100 N/m executes SHM. Its angular frequency and frequency are
A5π rad/s, 100 HzB10 rad/s, π5 HzC10 rad/s, 10π HzD10 rad/s, 5π HzThe time period of an oscillating spring of mass 630 g and spring constant 100 N/m with a load of 1 kg is
A0.2πsB0.21πsC0.22πsD0.02πs
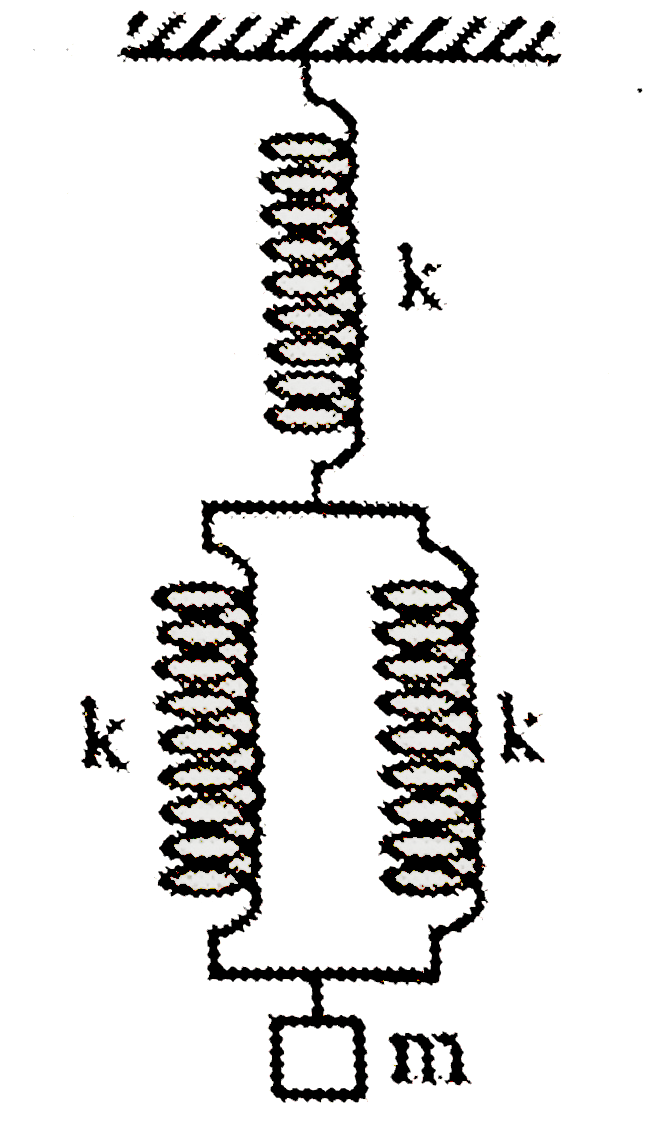
Two identical springs of spring constant '2k' are attached to a block of mass m and to fixed support (see figure).When the mass is displaced from equilibrium position on either side, it executes simple harmonic motion. The time period of oscillations of this sytem is :

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA body of mass m = 2kg hangs from three springs, each of spring constant 1875 N/m, as shown in the figure. If the mass is slightly displaced and let go, the system will oscillate with time period
View SolutionA mass of 4 kg suspended from a spring of spring constant 800Nm−1 executes simple harmonic oscillations. If the total energy of the oscillator is 4 J, the maximum acceleration (in ms−2) of the mass is
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View Solution
