A current-carrying ring is placed in a magnetic field. The direction of the field is perpendicular to the plane of the ring
(i) There is no net force on the ring
(ii) The ring will tend to expand
(iii) The ring will tend to contract
(iv) Either (ii) or (iii) depending on the directions of the current in the ring and the magnetic field
(i), (ii)
(ii), (iv)
(ii), (iii)
(i), (iv)
The correct Answer is:D
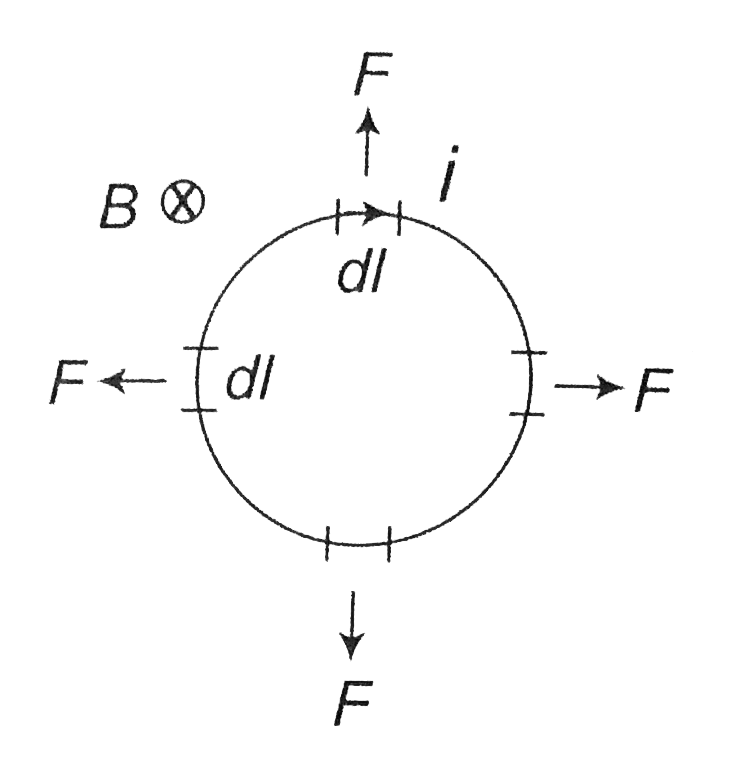
The ring will expand
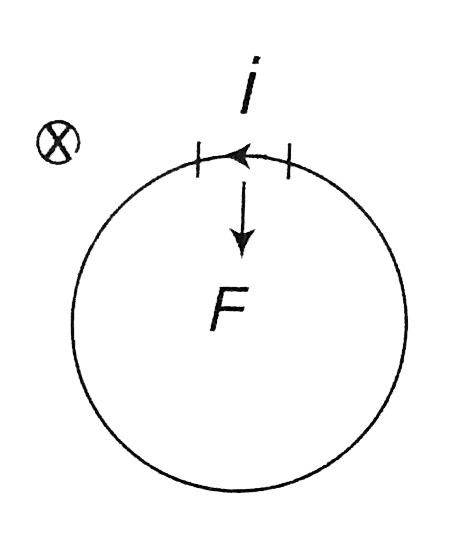
The ring will contract
(Fnet)loop=0
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the graph variation of magnetic field with time 't' applied perpendicular to the plane of the ring is shown:
 Aat t=2 sec and current flowing in ring is equal to zeroBcurrent wil change its direction two times in time intervals t=0 to t=8 secCcurrent will change its direction only once in the above intervalDflux in ring is same at t=0 and t=4 sec
Aat t=2 sec and current flowing in ring is equal to zeroBcurrent wil change its direction two times in time intervals t=0 to t=8 secCcurrent will change its direction only once in the above intervalDflux in ring is same at t=0 and t=4 secA conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
AIt is rotated about it axisBit is translatedCit is rotated about a diameterDit is deformedA metal ring is placed in a magnetic field, with its plane ⊥ to the field. If the magnitude of the field begins to change, the ring will experience
Aa net forceBa torque about it axisCa torque about a diameterDa tension along its length
A conducting ring of radius r is placed in a varying magnetic field perpendicular to the plane of the ring. If the rate at which the magnetic field varies is x, the electric field intensity at any point of the ring is
View SolutionA current carrying ring is placed in a horizontal plane. A charged particle is dropped along the axis of the ring to fall under the influence of gravity
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r change ate the rate dBdt
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
View SolutionA circular ring of radius r is placed in a homogeneous magnetic field perendicular to the plane of the ring. The field B changes with time according to the equation B=kt where K is constant and r is the time. The electric field in the ring is:
View Solution

