A circular loop of radius r carrying a current i is held at the centre of another circular loop of radius R(gtgtr) carrying a current I. The plane of the smaller loop makes an angle of 30∘ with that of the larger loop. It the smaller loop is held fixed in this position by applying a single force at a point on its periphery, what would be the minimum magnitude of this force?
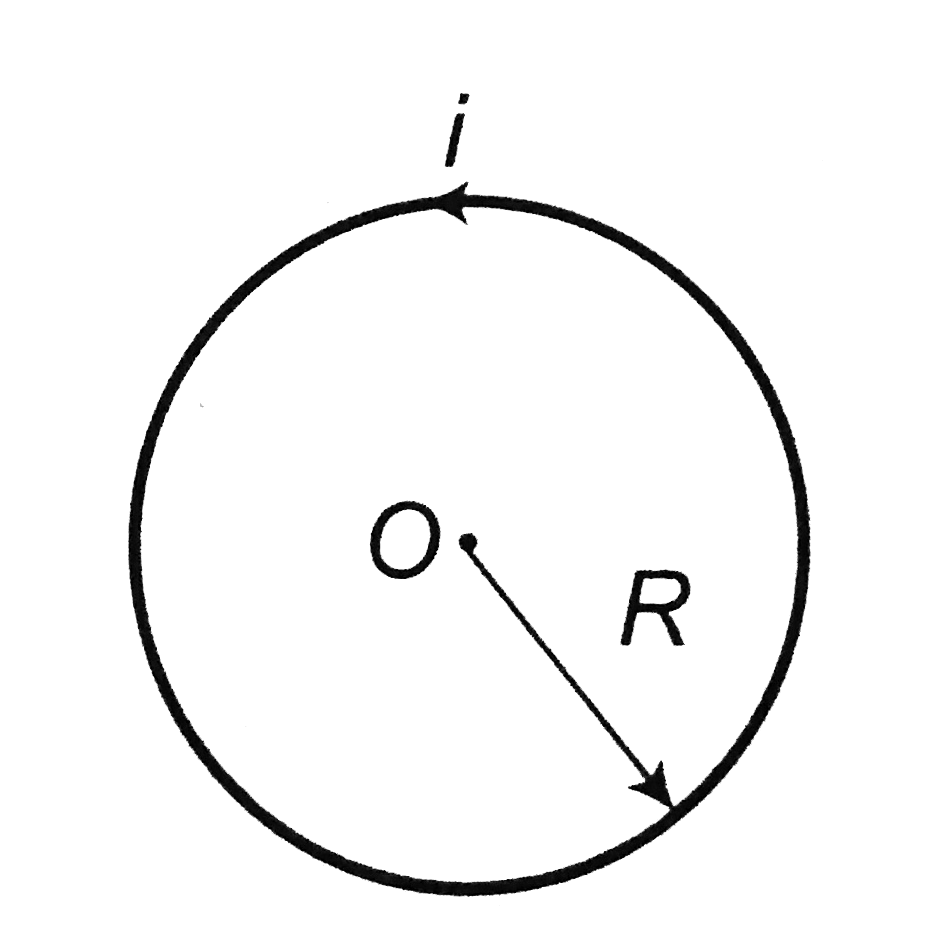
Magnetic field at centre
B=μ0i2R,⊙
Magnetic moment of circular loop of radius r
M=i0.πr2, perpendicular to plane of loop
The angles between planes of loop is 30∘ and hence angle between M and B is also 30∘.
Torque acting on circular loop of radius r
τ=MBsinθ
=i0πr2.μ0i2Rsin30∘
=μ0i0πr24R
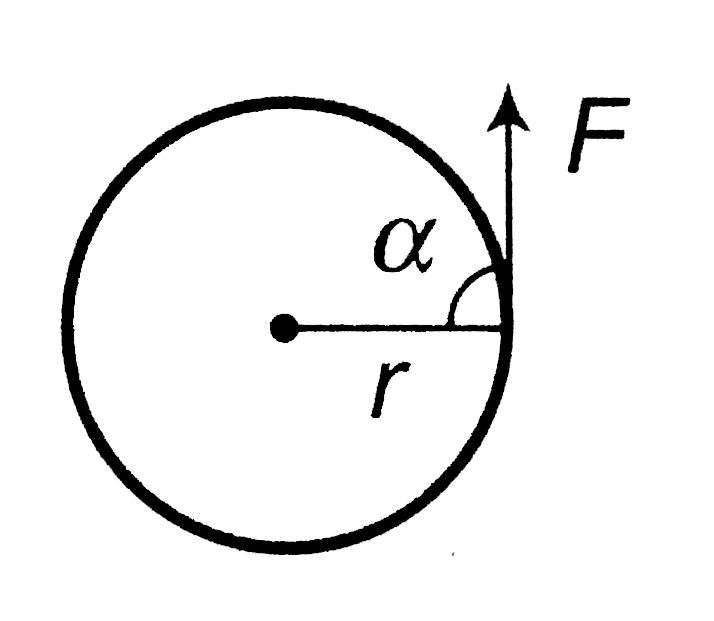
Torque applied by single force
τ'=rFsinα α: angle between →r and →F
τ'=τ
rFsinα=μ0i0iπr24R
F=μ0i0iπr4Rsinα
F is minimum if sinα=1⇒α=90∘
Fmin=μ0i0iπr4R
Topper's Solved these Questions
Similar Questions
A circular loop of radius r carrying a current i is held at the centre of another circular loop of radius R(>> r) carrying a current I. The plane of the smaller loop makes an angle of 30∘ with that of the larger loop. It the smaller loop is held fixed in this position by applying a single force at a point on its periphery, what would be the minimum magnitude of this force?
View SolutionA circular loop of radius R carries a current I. Another circular loop of radius r(ltltR) carries a current I. The plane of the smaller loop makes an angle of 30^@ with that of the larger loop. The planes of the two circles are at right angle to each other. Find the torque acting on the smaller loop.
View Solution
Knowledge Check
Magnetic field intensity H at the centre of a circular loop of radius r carrying current I e.m.u. is
ArI oerstedB2πr oerstedCI2πr oerstedD2πrI oerstedMagnetic induction produced at the center of a circular loop of radius R carrying a current is 'B' The magnetic moment of the loop is
Ahigh susceptibility and low retentivityBlow susceptibility and high retentivityClow susceptibility and low retentivityDhigh susceptibility and high retentivityA circular loop of radius 0.05 m carries a current of 1.0 A. The magnetic moment of the loop is .
A1.32×10−4A−m2B7.85×10−4A−m2C2.62×10−4A−m2D5.25×10−4A−m2
What is the magnetic moment of a circular loop of radius R carrying current I clockwise?
View SolutionA square loop of side a carries a current I. The magnetic field at the center of the loop is
View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View SolutionA long straight conductor carrying a current i is bent to form an almost complete circular loop of radius r on it. The magnetic field at the centre of the loop

View SolutionA circular loop carrying a current is replaced by an equivalent magnetic dipole. A point on the loop is in
View Solution