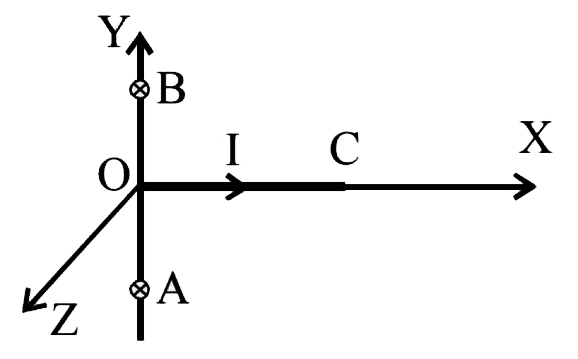
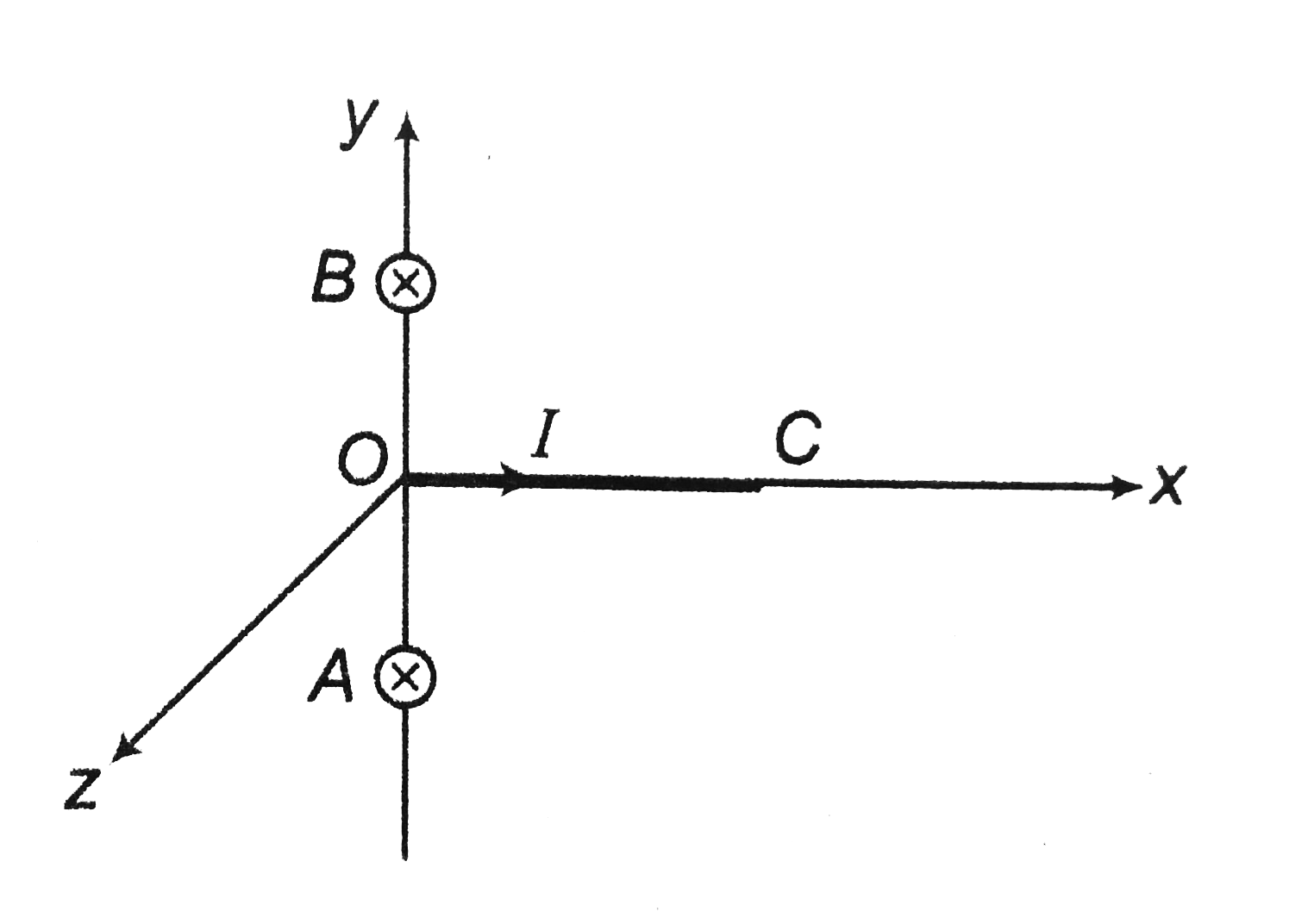
A straight segment OC(of length L meter) of a circuit carrying a current Iamp is placed along the x−aξs ( fig.). Two infinetely long straight wires AandB , each extending from z=−∞→+∞, are fixed at y=−ameterandy=+ameter respectively, as shown in the figure.
If the wires AandB each carry a current Iamp into the plane of the paper, obtain the expression for the force acting on the segment OC. What will be the force on OC if the current in the wire B is reversed?
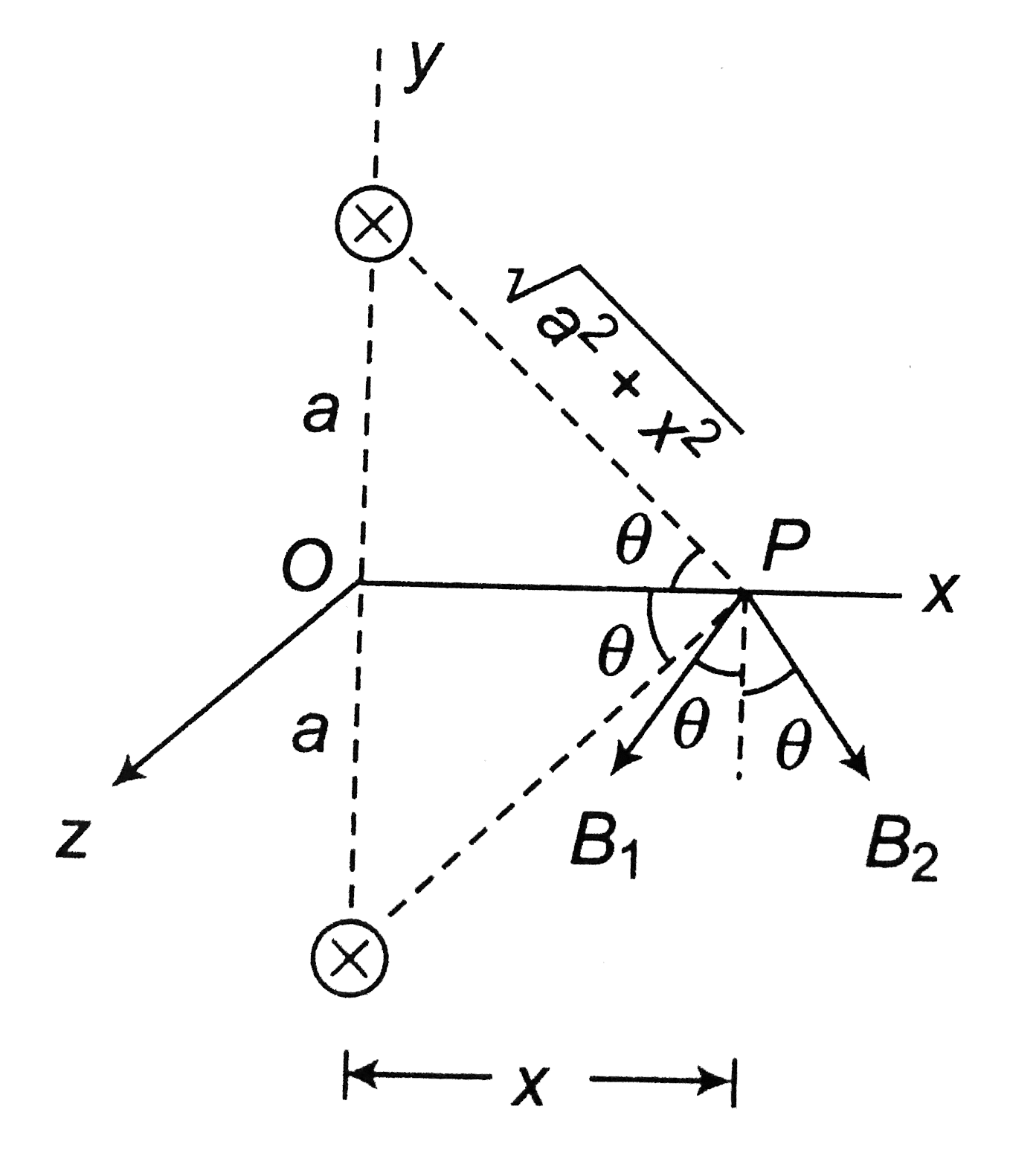
Magnetic field at distance x from O
B1=B2=μ0i2π(a2+x2)1/2=B
BP=2Bcosθ=2×μ0i2π(a2+x2)1/2×x(a2+x2)1/2
=μ0ixπ(a2+x2), downward
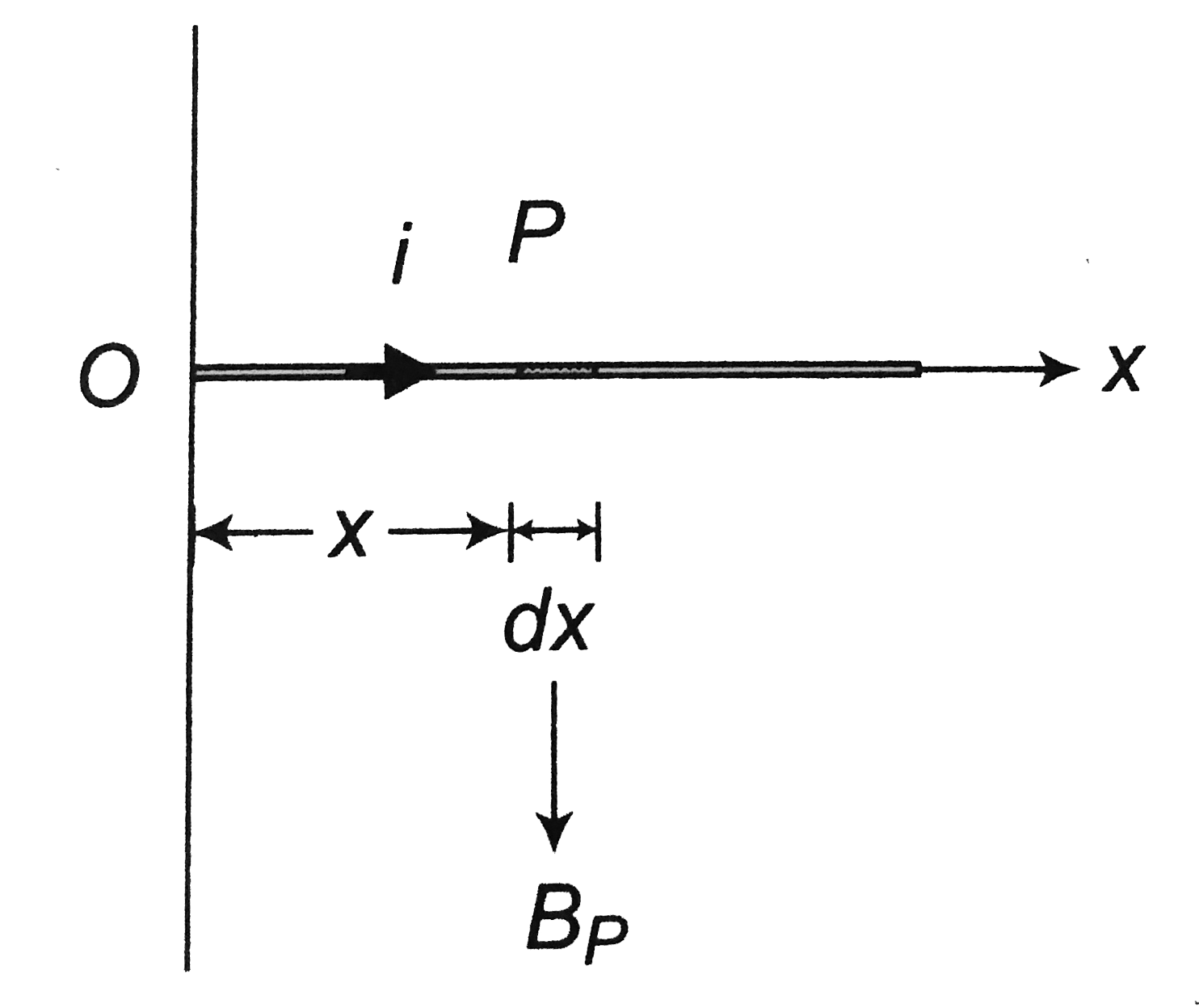
Consider a length dx of wire at distance x,
dF=BPidx
=μ0ixidxπ(a2+x2)
F=μ0i2π∫L0xdx(a2+x2)
I=∫L0xdxa2+x2
Let a2+x2=t2
xdx=tdt
=∫tdtt2=∫dtt=loget=∣∣loge√(a2+x2)∣∣L0
=loge(a2+L2)1/2−loge(a)=loge(√a2+L2a)
=12loge(a2+L2a2)
F=μ0i22πloge(a2+L2a) along −z direction
If current in wire B is reversed
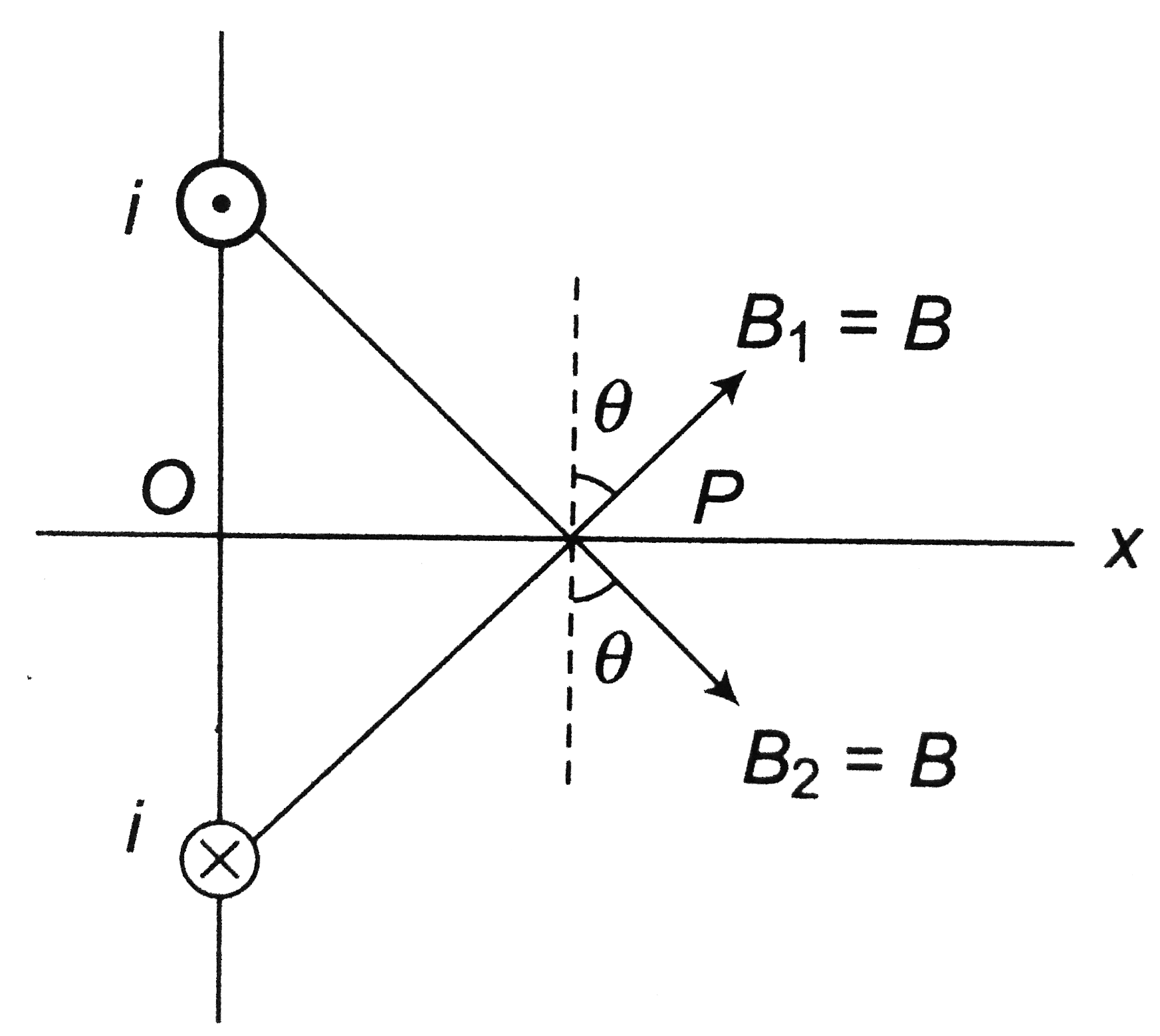
BP=2Bsinθ along x- axis.

Since current and magentic field are in same direction, hence force =0.
Note: For medical aspirants, this type of integral can be ignored.
Topper's Solved these Questions
Similar Questions
A straight segment OC (of lengh L) of a circuit carrying a current I is placed along the x-axis. Two infinitely long straight wire A and B each extending from z=−∞→+∞ are fixed at y=−a and y=+a respectively as show in the figure. If the wires A and B each carry a current I into the plane of the paper, obtain the expression for the force acting on the segment OC. What will be the force on OC if the current in the wire B is reversed?
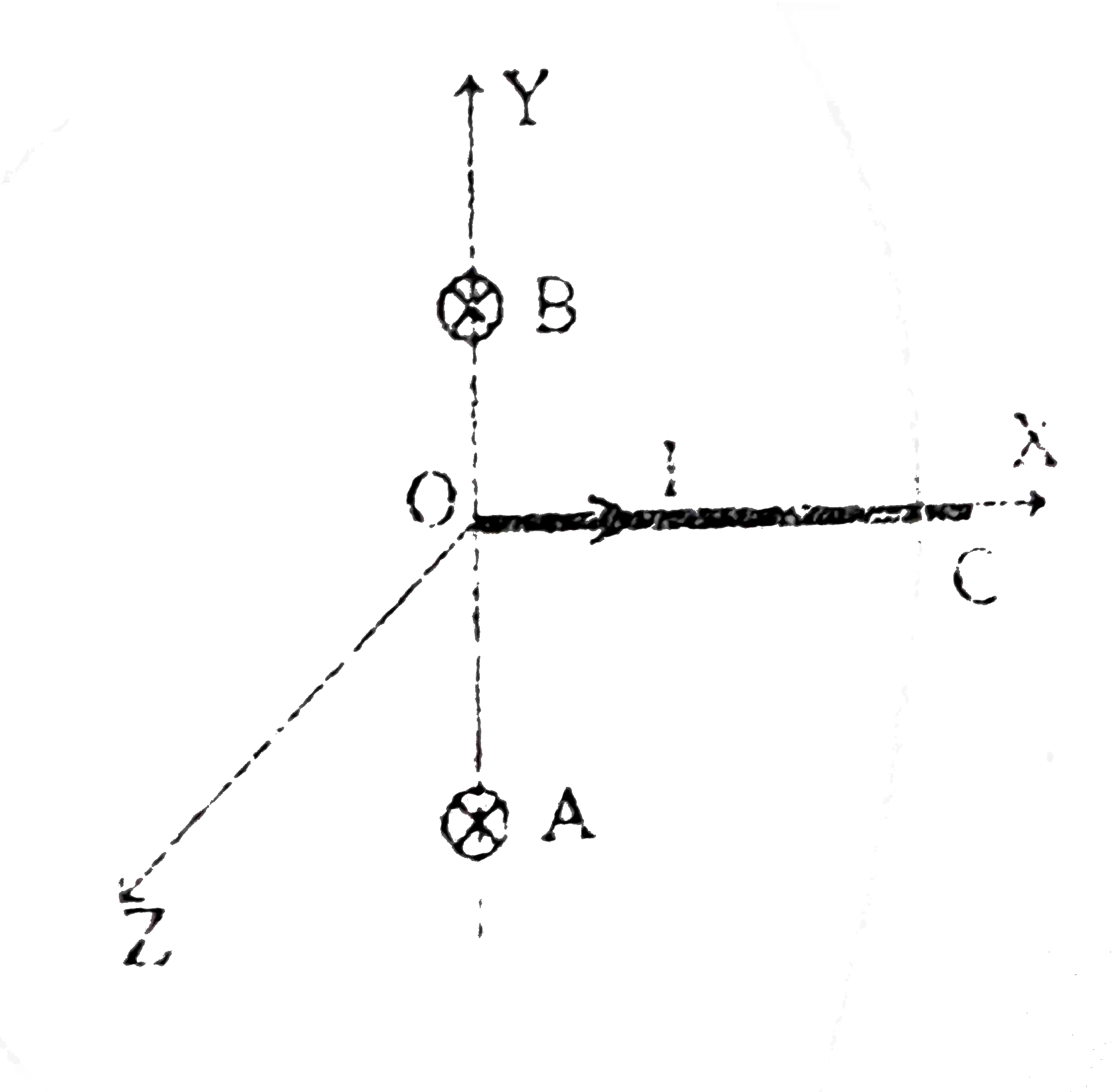
View SolutionA stright segment OC (of length L meter) of a circuit carrying a current 2amp is placed along the x-axis.Two infinitely long straight wires A and B each extending form z=∞to+∞, are fixed at y=−ametre and y=+ametre respectively, as shown in the figure.If the wires A and B each carry a current I amp into plane of the paper.Obtain the expression for the force acting on the segment OC.The force on OC is (μ0Nπ)ln(L2+a2a2)(−ˆk).Then find the value of N
View Solution
Knowledge Check
A straight wire carrying current is parallel to the y-axis as shown in Fig. The
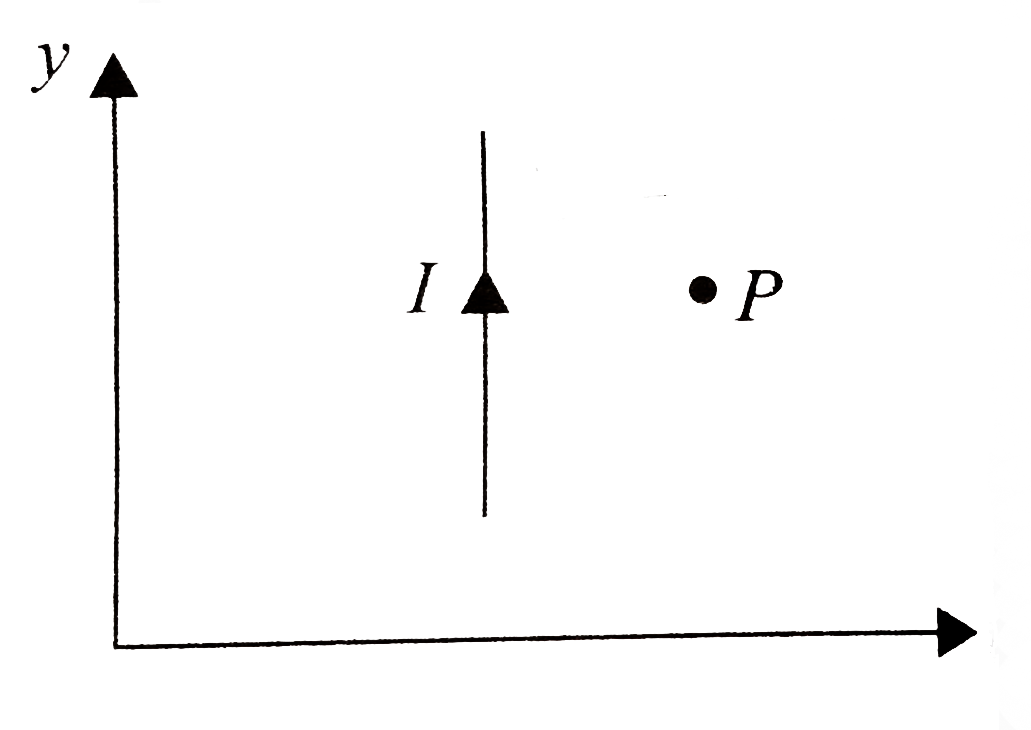 Amagnetic field at the point P is parallel to the x-axis.Bmagnetic field at P is along z-axisCmagnetic field are concentric circle with the wire passing through their common centreDmagnetic fields to the left and right of the wire and oppositely directed.
Amagnetic field at the point P is parallel to the x-axis.Bmagnetic field at P is along z-axisCmagnetic field are concentric circle with the wire passing through their common centreDmagnetic fields to the left and right of the wire and oppositely directed.There is a circular loop carrying current and another straight wire carrying current is placed along its axis. The straight wire
Awill apply radial inward force on the circular loop.Bwill apply radial outward force on the circular loop.Cwill apply force radially inward or outward, depending on the direction of currents.Dwill not exert any force on the circular loop.A current- carrying straight wire is kept along the axis of a circular loop carrying a current. The straight wire
Awill exert an inward force on the circular loopBwill exert an outward force on the circular loopCwill not exert any force on the circular loopDwill exert a force on the circular loop parallel to itself.
Two straight infinitely long current carrying wires are kept along Z-axis at the coordinates (0,a,0) and (0, -a, 0) respectively, as shown in the figure. The current in each of the wire is equal and along negative Z-axis (into the plane of the paper).
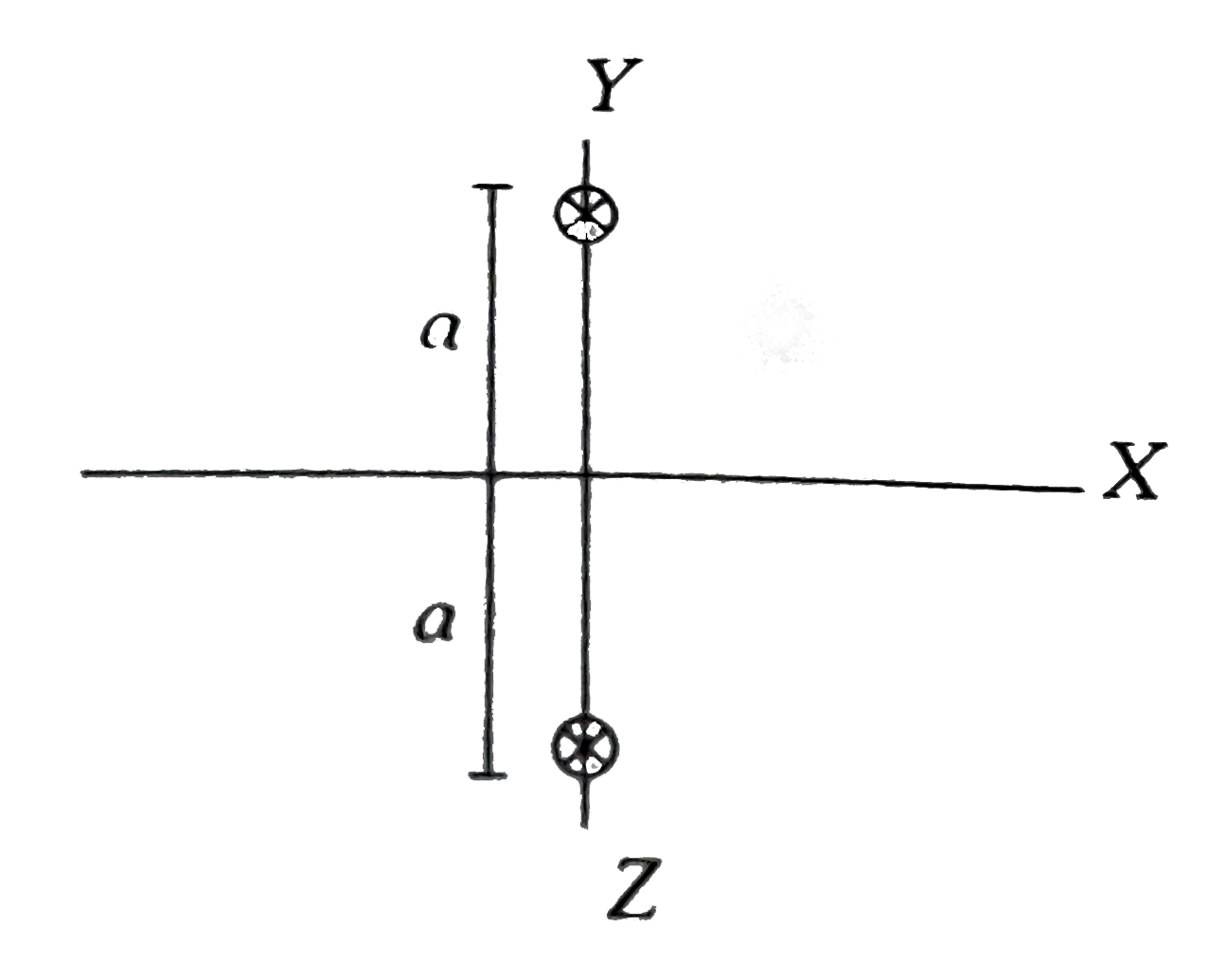
The variation of magnetic field on the X-axis will be approximately
View SolutionA current-carrying, straight wire is kept along the axis of a square loop carrying a current.The straight wire
View SolutionTwo infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is

View SolutionA long straight wire carrying current I and a square conducting wire loop of side l , at a distance 'a' from current wire as shown in the figure. Both the current wire and loop are in the plane of paper. Find the magnetic flux of current wire, passing through the loop.
View SolutionThe field due to a long straight wire carrying a current I is proportional to
View Solution
