A particle of mass m and charge q is lying at the origin in a uniform magnetic field B directed along x-axis. At time t = 0, it is given a velocity v0, at an angleθ with the y-axis in the xy-plane. Find the coordinates of the particle after one revolution.
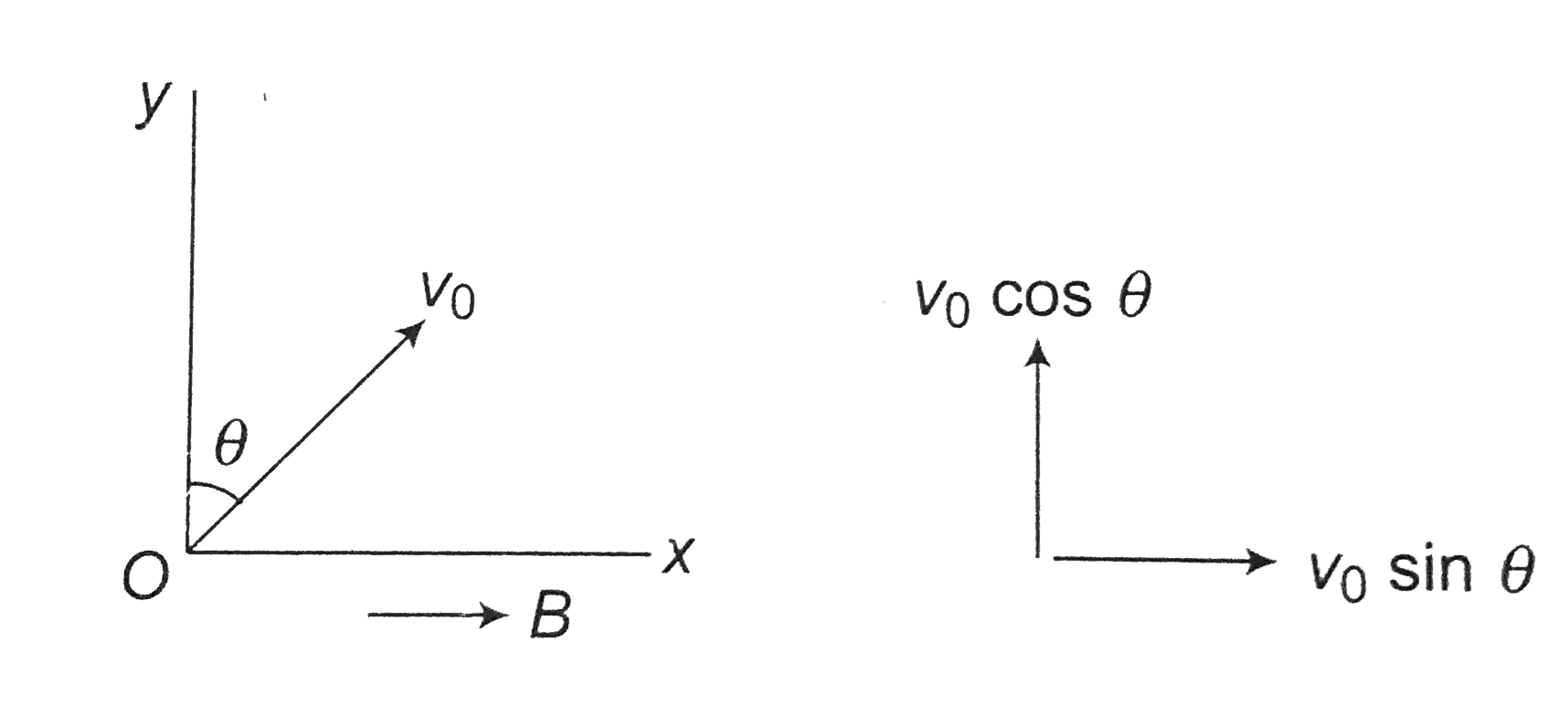
R−mv0cosθBq,T=2πmBq
Pitch x=v0sinθT=v0sinθ2πmBq
After every time t=nT,n=0,1,2,… particle touches x-axis.
After time t=T:
x=2πmv0sinθBq,y=z=0
(b) K=12mv2=qV
v=√2qVm
Pitch of helical path
p=vcosθT
As θ is small, cosθ≅1
p=vT=√2qVm.2πmBq
=√8π2mVqB2=√8π2mVeB2
Topper's Solved these Questions
Similar Questions
A particle of charge q and mass m is prjected in a uniform and contant magnetic field of strength B.The initial velocity →v makes angle θ with the →B.Find the distance travelled by the particle in time t.
View SolutionConsider the motion of a positive point charge in a region where there are simultaneous uniform electic and magnetic field E=E0ˆj and B=B0ˆj. At time t=0, this charge has velocity v inn the xy-plane making an angle θ with the x-axis. Which of the following option(s) is (are) correct for time t>0?
If θ=00 the charge moves in a circular path in the xy-plane.
b.Ifθ=00 the charge undergoes helical motion with constant pitch along the y-axis.
c. If θ=100 the charge undergoes helicalmotion with its pitch increasing with time along the y-axis.
d If θ=90∘ the charge undergoes linear but accelerated motion along the y-axis.
View Solution
Knowledge Check
A particle of mass m, carrying a charge q, is lying at the origin in a uniform magentic field directed along X axis. At the instant t = 0 it is given a velocity va at an angle θ with the y-axis, in the XY plane. The coordinates of the particle after two revolution will be
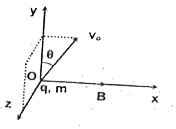 A(0,02πmv0sinθqB)B(2πmv0sinθqB,0,0)C(4πmv0sinθqB,0,0)D(0,0,0)
A(0,02πmv0sinθqB)B(2πmv0sinθqB,0,0)C(4πmv0sinθqB,0,0)D(0,0,0)A charged particle is fired at an angle θ to a uniform magnetic field directed along the x-axis. During its motionalong a helical path, the particle will
Anever move parallel to the x-axisBmove parallel to the x-axis once during every rotation for all velues of θCmove parallel to the x-axis at least once during every rotation if θ=45∘Dnever move perpendicular to the x-directionIn a certain region uniform electric field E and magnetic field B are present in mutually opposite directions. At the instant t=0, a particle of mass m carrying a charge q is given velocity v0 at angle θ, with the y− axis, in the yz plane. The time after which the speed of the particle would be minimum is equal to
 AmV0qEBmV0sinθqECmV0cosθqED2πmqB
AmV0qEBmV0sinθqECmV0cosθqED2πmqB
A particle having mass m and charge q is released from the origin in a region in which ele field and magnetic field are given by B=−B0ˆjand E=E0ˆk.
Find the y- component of the velocity and the speed of the particle as a function of it z-coordinate.
View SolutionA charged particle is fired at an angle θ to a uniform magnetic field directed along the x−axis. During its motion along a helical path, if the pitch of the helical path is equal to the maximum distance of the particle from the x− axis
View SolutionIn a certain region uniform electric field E and magnetic field B are present in mutually opposite directions. At the instant t=0, a particle of mass m carrying a charge q is given velocity v0 at angle θ, with the y− axis, in the yz plane. The time after which the speed of the particle would be minimum is equal to

View SolutionA particle of mass 'm' and charge 'q' is incident on XZ plane with velocity 'v' in a direction making angle θ with a uniform magnetic field applied along X-axis. The magnetic field applied along X-axis. The nature of motion performed by the particle is
View SolutionA particle of charge -q and mass m enters a uniform magnetic field →B (perpendicular to paper inward) at P with a velocity v0 at an angle α and leaves the field at Q with velocity v at angle β as shown in fig.
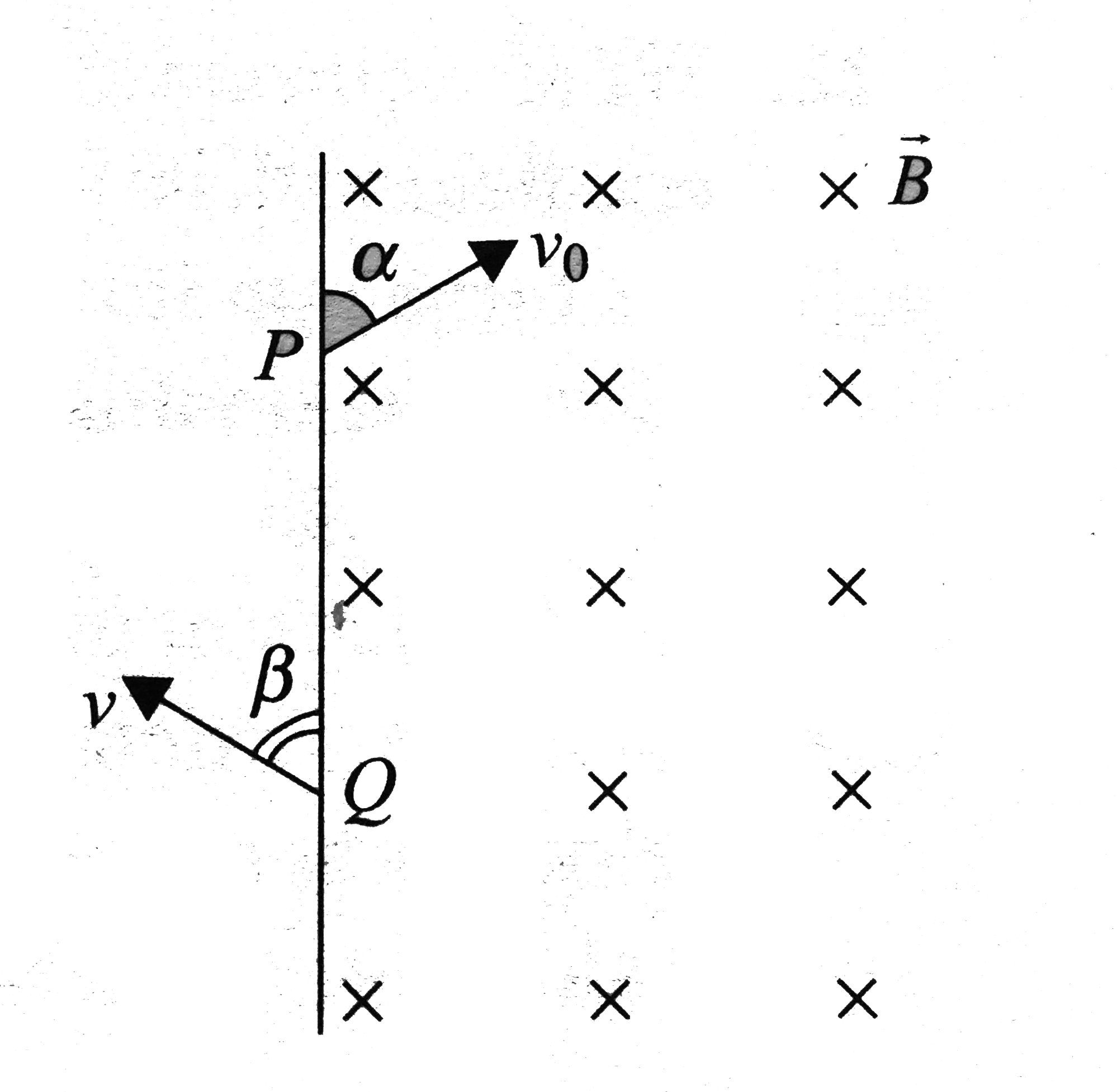
View Solution
