A tightly-wound, long solenoid has n turns per unit length, a radius r and carries a current i. A particle having charge q and mass m is projected from a point on the axis in a direction perpendicular to the axis. What can be the maximum speed for which the particle does not strike the solenoid?
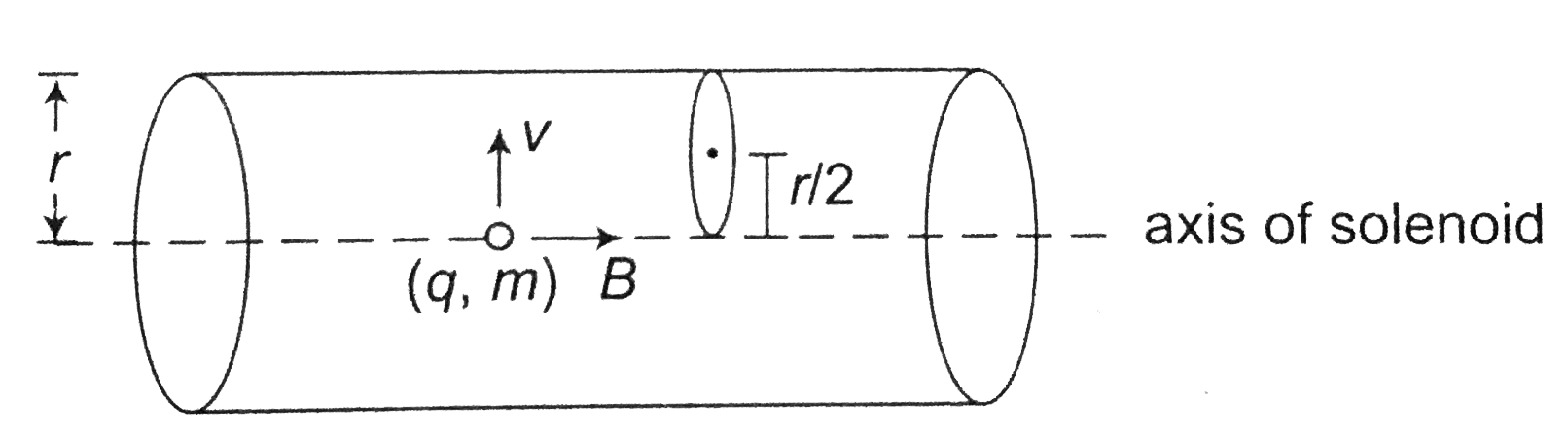
Magnetic field B=μ0ni, along axis of solenoid.
Since v is ⊥ar to B, particle moves in a circle of radius
R=mvBq=mvμ0niq
If particle does not strike solenoid
R≤r2
mvμ0niq≤r2
v≤μ0niqr2m
vmax=μ0niqr2m
Topper's Solved these Questions
Similar Questions
There is one long solenoid with turns per unit length. The radius of the solenoid is R and current flowing through it is I. There is a charged particle having charge q and mass m projected from a point on axis of the solenoid, and in a direction perpendicular to the axis. Find the maximum possible speed with which the charged particle can be projected so as not to strike the solenoid.
View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.
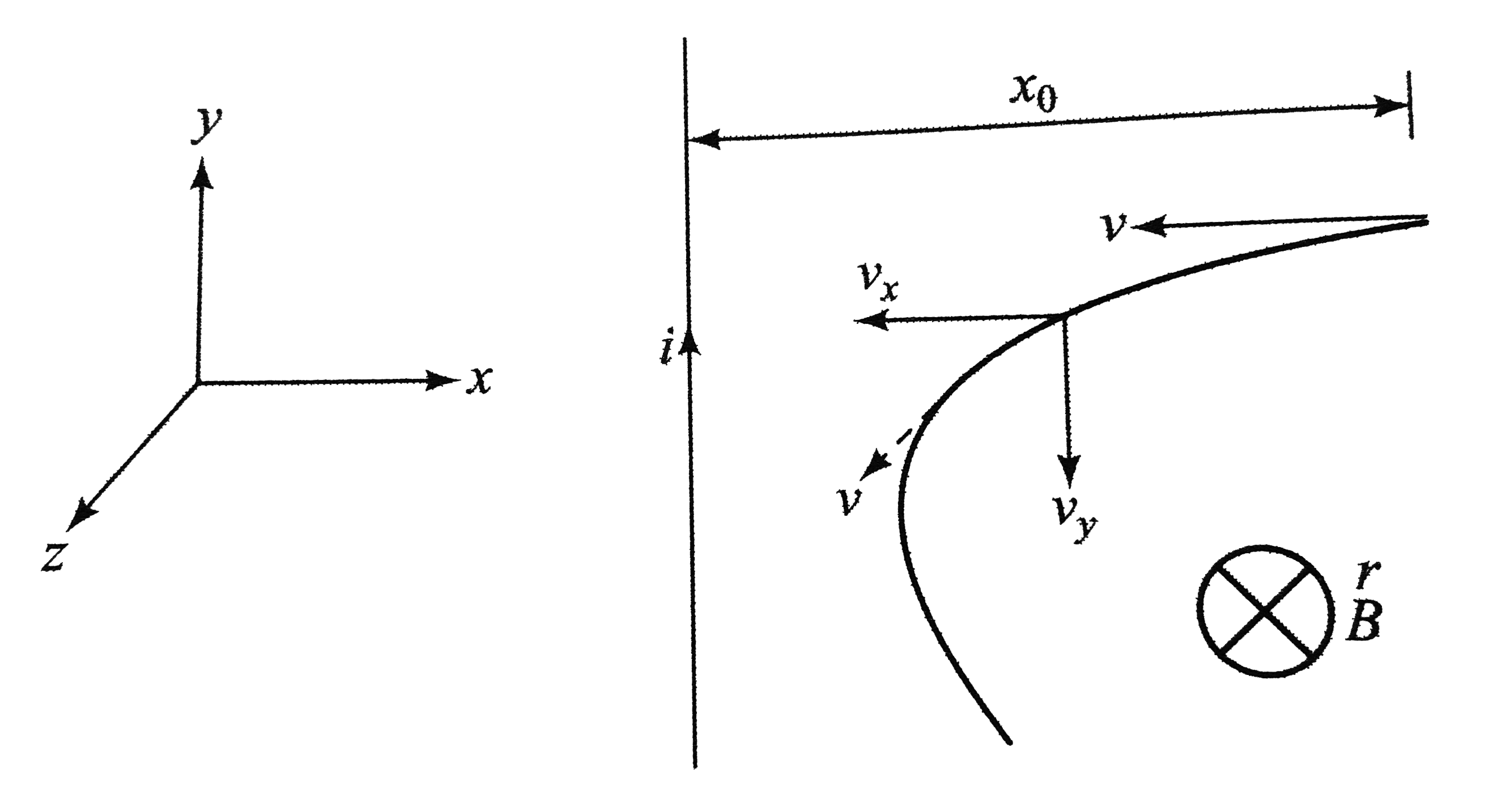

View Solution
Knowledge Check
The magnetic field on the axis of a long solenoid having n turns per unit length and carrying a current is
Aμ0niBμ0n2iCμ0ni2Dnone of theseThe magnetic field B within the solenoid having n turns per unit length and carrying a current I is given by
Aμ0nIB4πμ0nICnIDμ0nIlThere is a long solenoid of radius 'R' having 'n' turns per unit length with current i flowing in it. A particle having charge 'q' and mass 'm' is projected with speed 'v' in the perpendicular direction of axis from a Point on its axis. Find maximum value of 'v' so that it will not collide with the solenoid.
ARqμ0ni2mB2Rqμ0nimCRqμ0ni3mDRqμ0ni4m
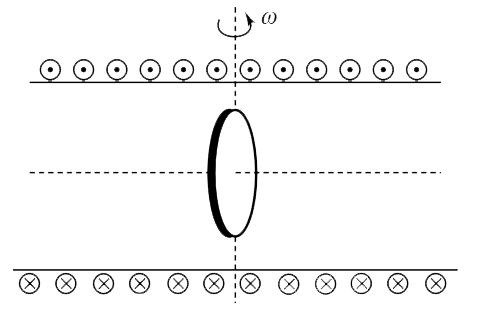
A long solenoid has n turns per unit length and carries a current i=i0sinωt. A coil of N turns and area A is mounted inside the solenoid and is free to rotate about its diameter that is perpendicular to the axis of the solenoid. The coil rotates with angular speed ω and at time t = 0 the axis of the coil coincides with the axis of the solenoid as shown in figure. Write emf induced in the coil as function of time.
View SolutionConsider the situation described in the previous example. A particle of mass m having a charge q is placed at a distance d from the metal sheet and is projected towards it. Find the maximum velocity of projection for which the particle does not hit the sheet.
View SolutionA solenoid of length 10 cm and radius 1 cm contains 200 turns and carries a current of 10 A. Find the magnetic field at a point on the axis at a distance of 10cm from the centre.
View SolutionA long solenoid has a radius a and number of turns per unit length is n. If it carries a current i, then the magnetic field on its axis is directly proportional to
View SolutionAn infinite long solenoid having n turns per unit length is shown in figure. The magnetic field at P, when a current I is flowing through it would be
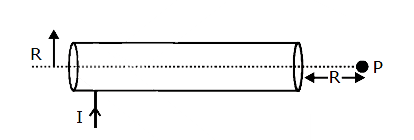
View Solution