A beam of charged particle, having kinetic energy 103eV, contains masses 8×10−27kgand1.6×10−26kg emerge from the end of an accelerator tube. There is a plate at distance 102m from the end of the tube and placed perpendicular to the beam. Calculate the magnitude of the smallest magnetic field which can prevent the beam from striking the plate.
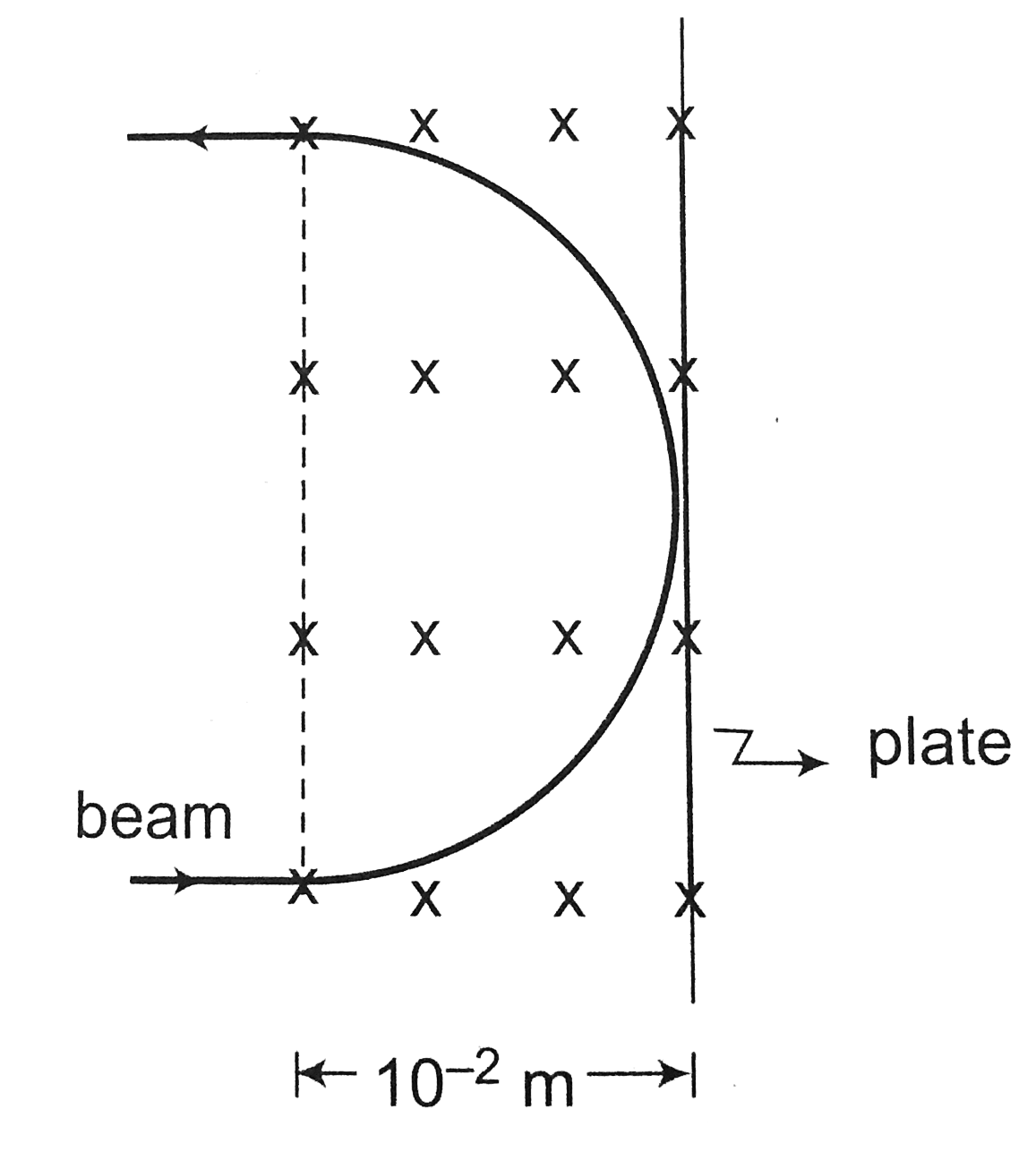
R=√2mKBq=√2mKBe
√2mKBe≤R(=0.01)
√2mKe(0.01)≤BorB≥√2mKe(0.01)
For minimum B, m should be greater, hence m=1.6×10−26kg
Bmin=√2×1.6×10−26×103×1.6×10−191.6×10−19(0.01)
=√2T
Topper's Solved these Questions
Similar Questions
A beam of charged particles having kinetic energy 103eV and containing masses 8×10−27kg and 1⋅6×10−26kg, emerges from the end of an accelerated tube. There is a plate at a distance 10−2m from the end of the tube and placed perpendicular to the beam. Calculate the magnitude of the smallest magnetic field which can prevent the beam from striking the plate.
View SolutionCalculate the magnitude of the electric field which can just balance a deuteron of mass 3.2×10−27kg
View Solution
Knowledge Check
A proton has a mass 1.67 ×10−27 kg and charge +1.6×10−19C. If the proton is accelerated through a potential difference of million volts, then the kinetic energy is
A1.6×10−15 JB1.6×10−13 JC1.6×10−21 JD3.2×10−13JA charged particle having charge 10−6 C and mass of 10−10 kg is fired from the middle of the plate making an angle 30∘ with plane of the plate. Length of the plate is 0.17m and it is separated by 0.1m. Electric field E=10−3NC is present between the plates. Just outside the plates magnetic field is present. Find the velocity of projection of charged particle and magnitude of the magnetic field perpendicular to the plane of the figure, if it has to graze the plate at C and A parallel to the surface of the plate. (Neglect gravity)
 A3.4mTB4.3mTC2.3mTD5.3mT
A3.4mTB4.3mTC2.3mTD5.3mTA particle of mass 1.6×10−27kg and charge 1.6×10−19 coulomb enters a uniform magnetic field of 1 Tesla as shown in the figure. The speed of the particle is 107m/s. The distance PQ will be
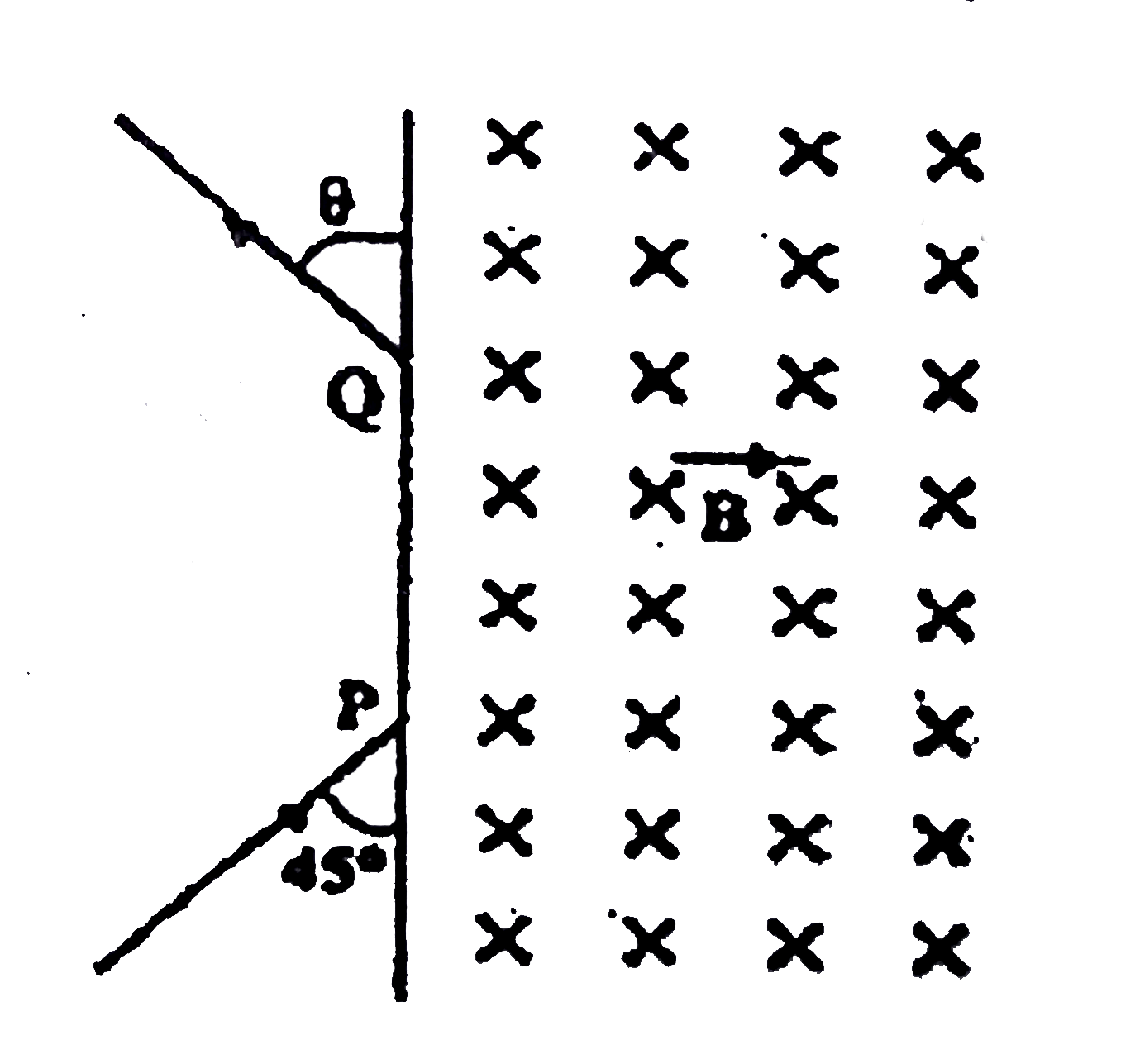 A0.14 mB0.28 mC0.4 mD0.5 m
A0.14 mB0.28 mC0.4 mD0.5 m
A laser beam has a wavelength of 7×10−7m and aperure 10−2m. The beam is sent to moon at a distance of 4×105km from earth. Find the angular spread and areal spread of the beam on reaching the moon.
View SolutionA laser beam has a wavelength of 6×10−7m and aperture of 6×10−2m. The beam is sent towards the moon which is at a distance of 4×108m from the earth. Calculate (i) angular spread of the beam and (ii) the arel spread when it reaches the moon.
View SolutionA beam of light has intensity 2.8×1014Wm−2 .Calculate the value of amplitude of electric field magnetic field of the beam .
View SolutionA charged particle having charge 10−6 C and mass of 10−10 kg is fired from the middle of the plate making an angle 30∘ with plane of the plate. Length of the plate is 0.17m and it is separated by 0.1m. Electric field E=10−3NC is present between the plates. Just outside the plates magnetic field is present. Find the velocity of projection of charged particle and magnitude of the magnetic field perpendicular to the plane of the figure, if it has to graze the plate at C and A parallel to the surface of the plate. (Neglect gravity)

View SolutionA charged particle having a mass of 1.6×10−26kg comes out of accelerator tube with kinetic energy 2×103eV . Calculate the smallest magnitude of the magnetic field that should be applied in vertically downwards direction to just prevent the charged particle from colliding the plate (Assume charge on particle = charge of the proton)
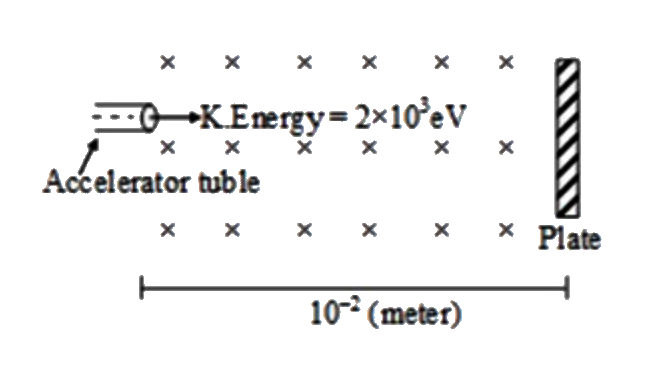
View Solution
