In YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S1and S2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S1 and S2 medium of refractive index n1=2 is present and to the right of S1 and S2 medium of n2=32, is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of n3 of the slab varies with distance from it's starting face as shown in figure.
Fringe width on the screen is
1μm
2μm
0.5μm
1.5μm
The correct Answer is:A
Area (A)=μ3(dx)=(1+3)t2=2t
Path difference
Δx=μ1SS2+μ2S2P−⎡⎢⎣μ1SS1+μ2S1P−t∫0(μ3−μ2)dx⎤⎥⎦
=μ1[SS2−SS1]+SS1+μ2[S2P−S1P]−t∫0μ3dx+t∫0μ2dx
In order to get central maxima at the centre 'O' of screen is Δx=0
O=2×(1×10−3)22×1+0−2t+32t
1×10−6=2t−3t2=t2t=2×10−6m⇒t=2μm
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - I(H.W)20videos
WAVE OPTICS
- BOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - II(H.W)19videos
WAVE OPTICS
- BOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - V37videos
WAVE OPTICS
- BOOK - NARAYNACHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - ADDITIONAL EXERCISE (ASSERTION AND REASON TYPE QUESTIONS :)19videos
SEMICONDUCTOR ELECTRONICS
Similar Questions
_PHY_E01_002_Q01.png)
Knowledge Check
- Question 1 - Select One
In YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S1and S2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S1 and S2 medium of refractive index n1=2 is present and to the right of S1 and S2 medium of n2=32, is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of n3 of the slab varies with distance from it's starting face as shown in figure.
In order to get central maxima at the centre of screen, the thickness of slab required is :A1μmB2μmC0.5μmD1.5μm - Question 2 - Select One
In YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S1and S2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S1 and S2 medium of refractive index n1=2 is present and to the right of S1 and S2 medium of n2=32, is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of n3 of the slab varies with distance from it's starting face as shown in figure.
If thickness of the slab is selected 1μm, then position of central maxima will be : (y-coordinate)A1/3 mmB−13mmC1/6 mmD−16mm - Question 3 - Select One
In YDSE arangement shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000∘Δ (in air). S1 and S2 are two slits separate by d=1mm and D=1m . Left of slits S1andS2 medium of refractive index μ1=2 is presernt refractive index μ2=32 is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of slab μ3 varies with distance from its starting face as shown in figure.
If the thickness of the slab is selected 1μm , then the position of the central maxima will be (y - coordinate)A13mmB−13mmC16mmD−16mm
Two coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :
View SolutionIn the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then
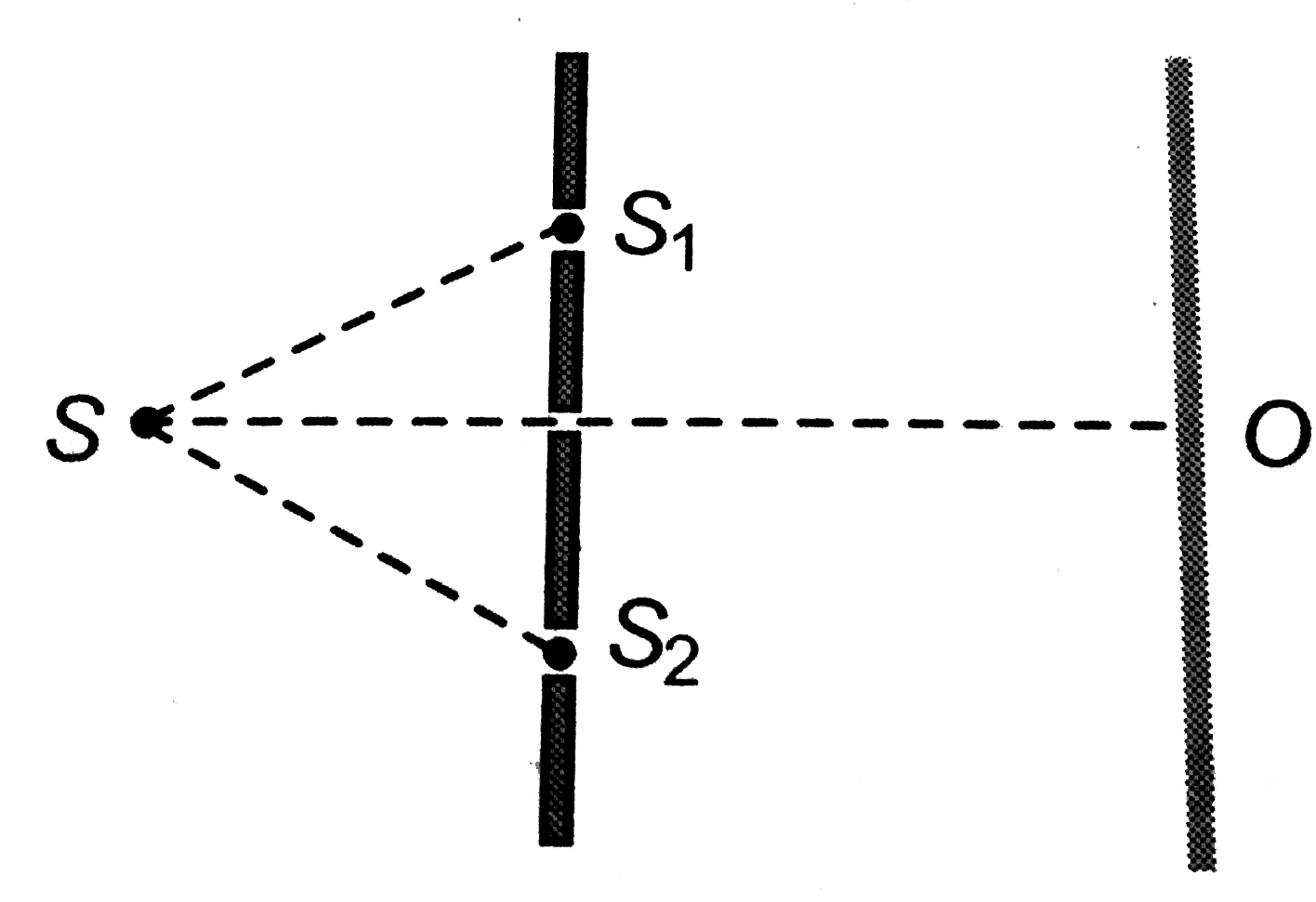
View Solution_S01_025_Q01.png)
In Young's double slit experiment the slits, S1&S2 are illuminated by a parallel beam of light of wavelength 4000 Å from the medium of refractive index n1=1.2 A thin film of thickness 1.2 μm and refractive index n=1.5 is placed infrom of S1 perpedicular to path of light. the refractive index of medium between plane of slits & screen is n2=1.4 if the light coming from the film and S1&S2 have equal intensities I then intensity at geometrical centre of the screen O isView SolutionIn arrangement shown in figure, plane wavefront of monochromatic light of wavelength λ is incident on identical slits S1 and S2. There is another pair of indentical slits S3 and S4 which are having separation Z=λD2d Point O is on the screen at the common perpendicular bisector of S1S2 and S3S4.I1 is the intensity at point O Now the board having slits S3S4 is moved upward parallel to itself and perpendicular to line AO till slit S4 is on line AO and it is observed that now intensity at point O is I2 then I2I1 is :
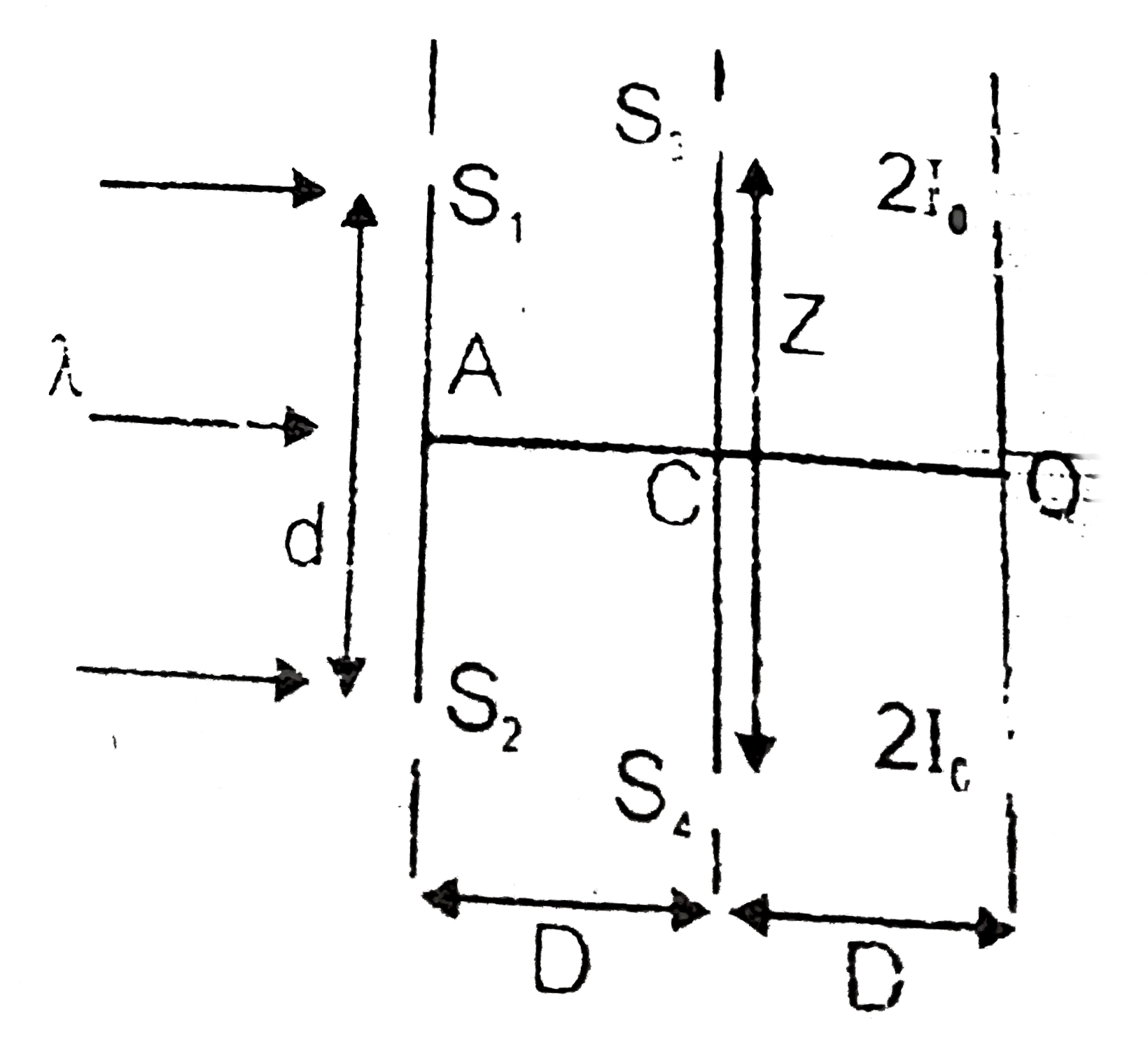
View SolutionIn a Young's double-slit experiment set up, source S of wavelength 6000Å illuminates two slits S1 and S2 which act two coherent sources. The sources S oscillates about its shown position according to the eqation y=1+cosπt, where y is in millimeter and t in second.
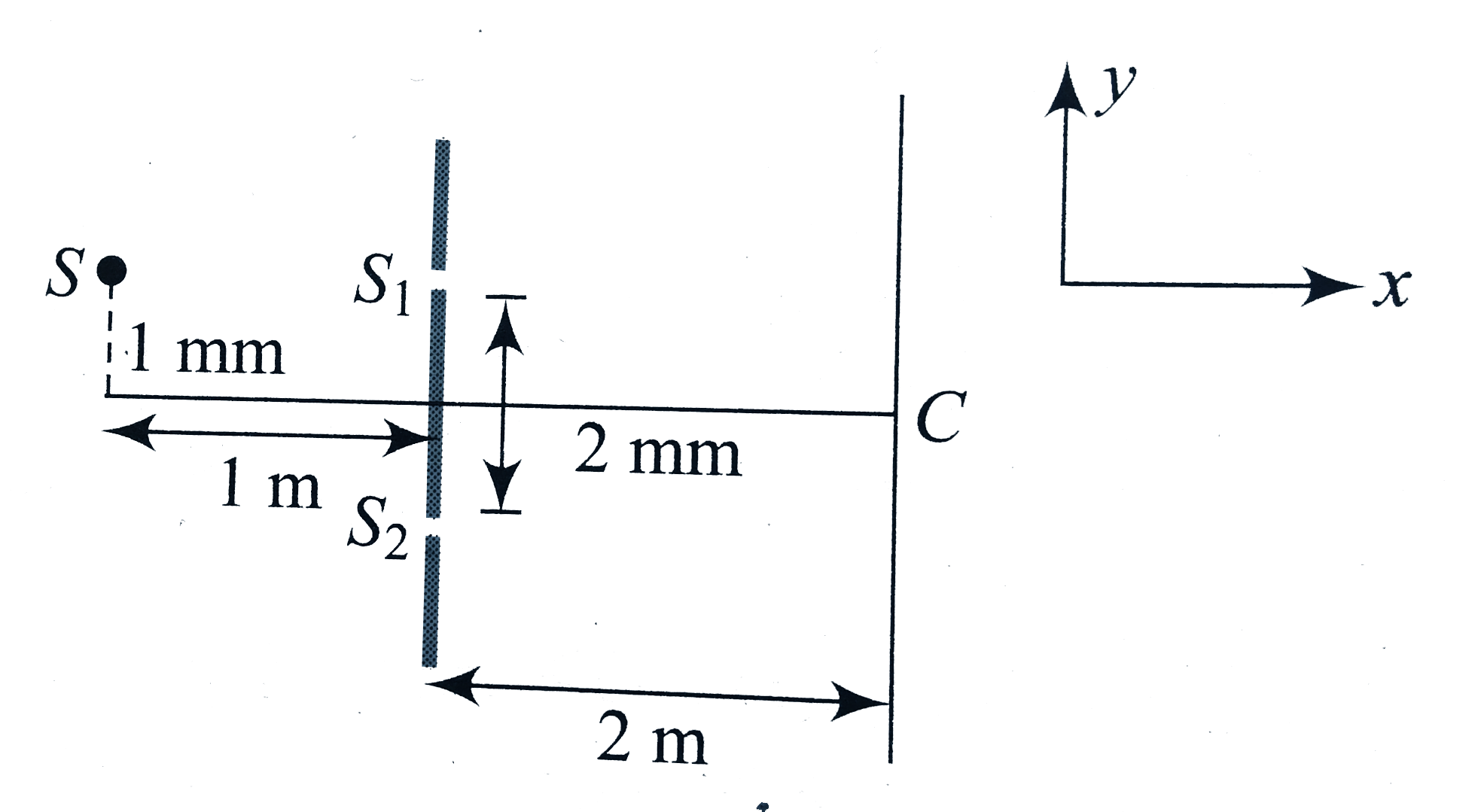
At t=1 s, a slab of thickness 2×10−3mm an refractive index 1.5 is placed just in front of S1. The central maximum is formed atView Solution