Two identical coherent sources are placed on a diameter of a circle of radius R at separation x (<<R) symmetrical about the center of the circle. The sources emit identical wavelength λ each. The number of points on the circle of maximum intensity is (x=5λ)
20
22
24
26
The correct Answer is:A
Path diff at P is , Δ=2(x/2cosθ)=xcosθ
For intensity to be maximum
Δx=nλ,xcosθ=nλ
nλx>1,x=5λ,n=1,2,3,4,5
Therefore in all for quadrants these can be 20 maximum
Topper's Solved these Questions
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - NCERT Based Questions
25 Videos
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - V
37 Videos
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - II (C.W)
31 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - NARAYNACHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - ADDITIONAL EXERCISE (ASSERTION AND REASON TYPE QUESTIONS :)
19 Videos
Similar Questions
Knowledge Check
Two identical coherent sources are placed on a diameter of a circle of radius R at a separation d(<<R)(d=nλ) symmetrically about the centre of the circle. The sources emit identical wavelength λ each. What will be the number of points on the circle with constructive interference?
A2n+1B4nC4n−2D4n+2Two sources of sound are placed along the diameter of a circle of radius R(R>>41). How many minima will be heard as one moves along the perimeter of circle.
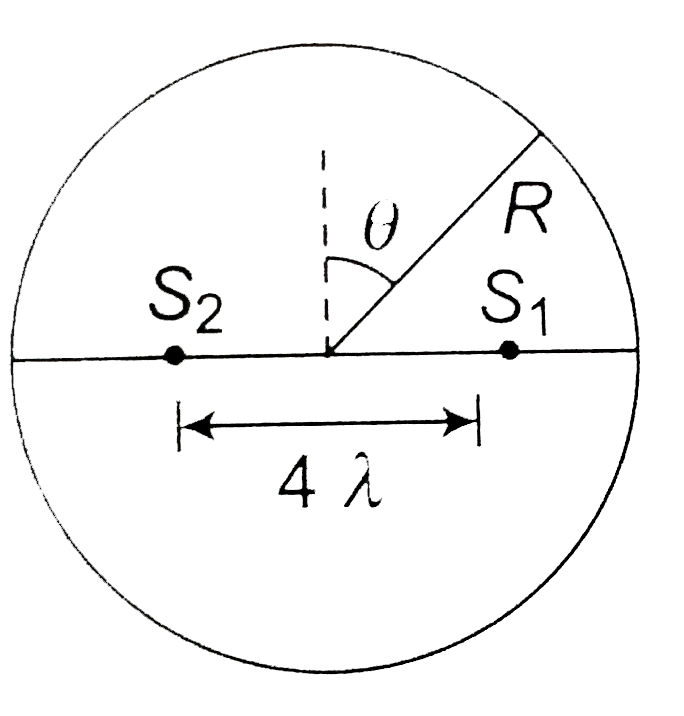 A12B16C4D20
A12B16C4D20If two coherent source are placed at a distance 3λ from each other, symmetric to the centre of the circel as shown in figure, Find thenumber of fringes shown on the screen, placed along the circumference ?
 A16B12C8D4
A16B12C8D4
Two coherent light sources A and B with separation 2λ or placed on the x-axis symmetrically about the origin. They emit light of wavelength λ. Obtain the positions of maxima on a circle of large radius, lying in the x-y plane and centre at the origin.
View SolutionIf the equations of the two diameters of a circle are x−y=5 and 2x+y=4 and the radius of the circle is 5, find the equation of the circle.
View SolutionLet PQandRS be tangent at the extremities of the diameter PR of a circle of radius r. If PSandRQ intersect at a point X on the circumference of the circle, then prove that 2r=√PQxRS .
View SolutionTwo identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
View SolutionTwo coherent sources S1 and S2 area separated by a distance four times the wavelength λ of the source. The sources lie along y axis whereas a detector moves along +x axis. Leaving the origin and far off points the number of points where maxima are observed is
View Solution
