The polaroids P1,P2&P3 are arranged coaxially. The angle between P1 and P2 is 37∘. The angle between P2 and P3 is, if intensity of emerging light is a quarter of intensity of unploarized light
θ=cos−1(54)
θ=cos−1(45)
θ=cos−1(45√2)
θ=cos−1(54√2)
The correct Answer is:D
To solve the problem involving three polaroids arranged coaxially, we will apply Malus's Law, which relates the intensity of polarized light transmitted through a polaroid to the angle between the light's polarization direction and the polaroid's axis.
1. Understanding the Initial Setup:
- We have three polaroids: P1, P2, and P3.
- The angle between P1 and P2 is given as 37∘.
- The light incident on P1 is unpolarized.
2. Intensity After P1:
- When unpolarized light passes through the first polaroid (P1), the intensity of the transmitted light is halved.
- Therefore, if I0 is the intensity of the unpolarized light incident on P1, the intensity after P1 (I1) is:
I1=I02
3. Intensity After P2:
- The intensity after passing through P2 can be calculated using Malus's Law:
I2=I1⋅cos2(θ)
- Here, θ is the angle between P1 and P2, which is 37∘.
- Substituting the values:
I2=I02⋅cos2(37∘)
4. Calculating cos2(37∘):
- We know that cos(37∘)≈0.8 (exact value is 45).
- Therefore:
cos2(37∘)=(45)2=1625
- Now substituting this back into the equation for I2:
I2=I02⋅1625=16I050=8I025
5. Intensity After P3:
- We know that the intensity of the emerging light from the system is given as a quarter of the initial intensity:
I3=I04
- Using Malus's Law again for P3:
I3=I2⋅cos2(ϕ)
- Here, ϕ is the angle between P2 and P3, which we need to find.
6. Setting Up the Equation:
- We can equate the two expressions for I3:
I04=8I025⋅cos2(ϕ)
- Canceling I0 from both sides:
14=825⋅cos2(ϕ)
7. Solving for cos2(ϕ):
- Rearranging gives:
cos2(ϕ)=2532
8. Finding ϕ:
- Taking the square root:
cos(ϕ)=√2532=5√32=54√2
- Finally, to find ϕ:
ϕ=cos−1(54√2)
Final Answer
The angle between P2 and P3 is ϕ=cos−1(54√2).
- We have three polaroids: P1, P2, and P3.
- The angle between P1 and P2 is given as 37∘.
- The light incident on P1 is unpolarized.
- When unpolarized light passes through the first polaroid (P1), the intensity of the transmitted light is halved.
- Therefore, if I0 is the intensity of the unpolarized light incident on P1, the intensity after P1 (I1) is:
I1=I02
- The intensity after passing through P2 can be calculated using Malus's Law:
I2=I1⋅cos2(θ)
- Here, θ is the angle between P1 and P2, which is 37∘.
- Substituting the values:
I2=I02⋅cos2(37∘)
- We know that cos(37∘)≈0.8 (exact value is 45).
- Therefore:
cos2(37∘)=(45)2=1625
- Now substituting this back into the equation for I2:
I2=I02⋅1625=16I050=8I025
- We know that the intensity of the emerging light from the system is given as a quarter of the initial intensity:
I3=I04
- Using Malus's Law again for P3:
I3=I2⋅cos2(ϕ)
- Here, ϕ is the angle between P2 and P3, which we need to find.
- We can equate the two expressions for I3:
I04=8I025⋅cos2(ϕ)
- Canceling I0 from both sides:
14=825⋅cos2(ϕ)
- Rearranging gives:
cos2(ϕ)=2532
- Taking the square root:
cos(ϕ)=√2532=5√32=54√2
- Finally, to find ϕ:
ϕ=cos−1(54√2)
The angle between P2 and P3 is ϕ=cos−1(54√2).
Topper's Solved these Questions
- WAVE OPTICSBook:NARAYNAChapter:WAVE OPTICSExercise:LEVEL - III
Explore 30 Videos
- WAVE OPTICSBook:NARAYNAChapter:WAVE OPTICSExercise:NCERT Based Questions
Explore 25 Videos
- WAVE OPTICSBook:NARAYNAChapter:WAVE OPTICSExercise:LEVEL - I (C.W)
Explore 38 Videos
- SEMICONDUCTOR ELECTRONICSBook:NARAYNAChapter:SEMICONDUCTOR ELECTRONICSExercise:ADDITIONAL EXERCISE (ASSERTION AND REASON TYPE QUESTIONS :)
Explore 19 Videos
Similar Questions
The polaroids P1 and P2 are placed in crossed position. A third polaroid P3 is kept between P1 and P2 such that pass axis of P3 is parallel to that of P1. How would the intensity of light (I2) transmitted through P2 vary as P3 is rotated ? Draw plot of intensity I2 versus angle θ between pass axis of P1 and P3. In which orientation will the transmitted intensity be minimum and maximum ?
View SolutionUnpolarized light is intensity I0 passes through two polaroids P1 and P2 such that pass axis of P2 makes an angle θ with the pass axis of P1. A third polaroid P3 is placed between P1 and P2 with pass axis of P3 making an angle β with that of P1. If I1,I2,I3 represent intensities of light trnasmitted by P1,P2,P3, determine the values of angle θ and β for which I1=I2=I3.
View Solution
Knowledge Check
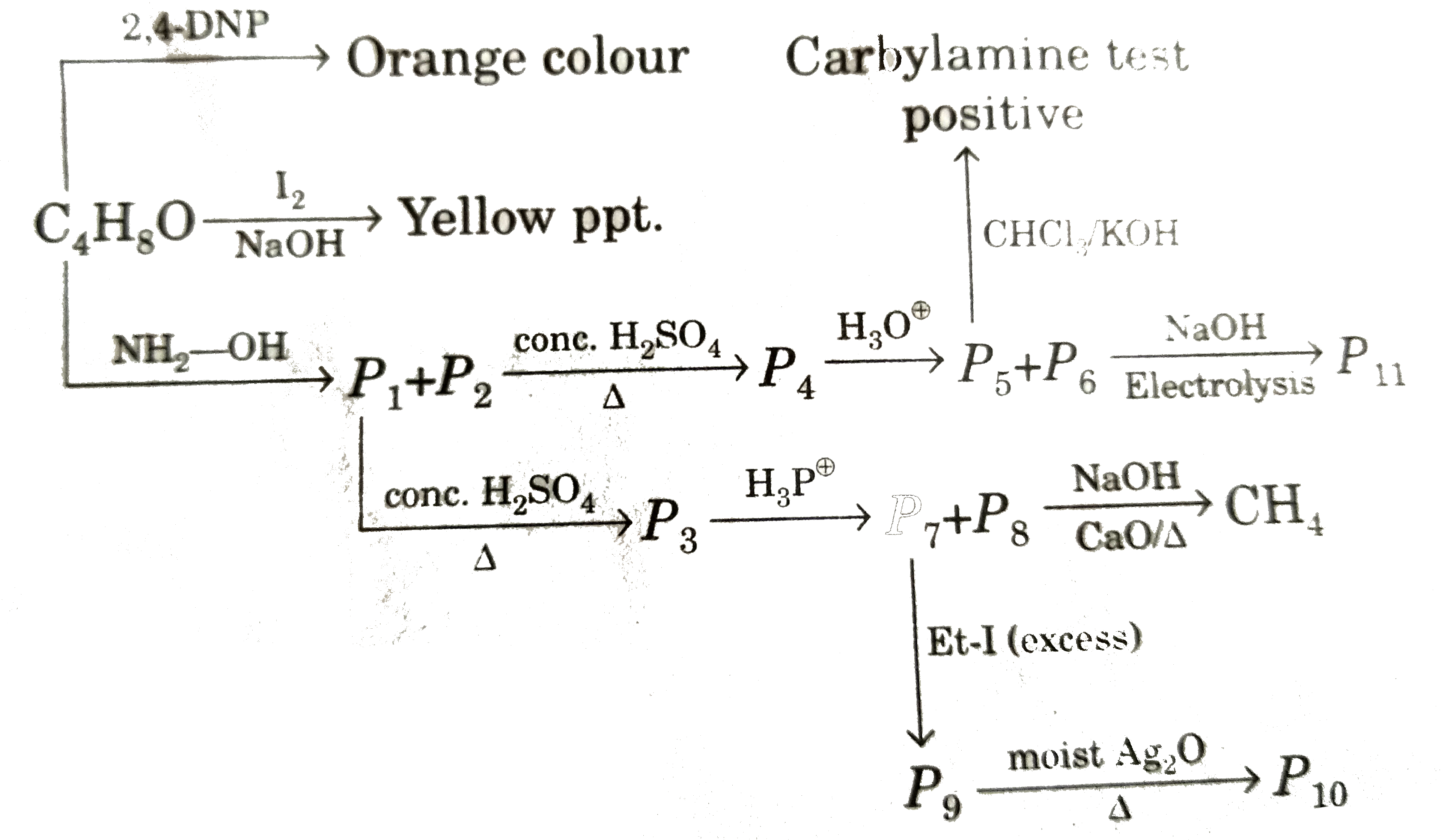
What is the relationship between P1 and P2AGeometrical isomersBOptical isormersCPositional isomersDChain isomersThe phase of a particle at P1 is 60∘ and the phase of a particle at P2 is 780∘. If the distance between P1andP2 is 1m, then the wavelength of the wave, will be
A2mB0.5 mC1.5 mD0.25 mThree identical conducting plates P1,P2 and P3 are kept at a distance d from each other. If q,-q,2q are the charges in P1,P2 and P3 respectively, the electric field between P1 and P2 is (where A is area of plate)
A(q2Aε0)B(2q2Aε0)C0D(4q2Aε0)
Two Polaroids P1 and P2 are placed with their axis perpendicular to each other. Unpolarized light I0 is incident on P1. A third polaroid P3 is kept in between P1and P2 such that its axis makes an angle 45∘ with that of P1. Then intensity of transmitted light through P2 is I0n. Find n.
View SolutionA plane P1 has the equation 4x−2y+2z=3andP2 has the equation −x+ky−2z=7. If the angle between P1 and P2 is 2π3, then the value of k can be
View SolutionGiven →p⋅(→P+→Q)=P2 then the angle between →Pand→Q is
View SolutionIf three parallel planes are given by
P1:2x−y+2z=6
P2:4x−2y+4z=λ
P3:2x−y+2z=μ
if distance between P1 and P2 is 13 and between P1 and P3 is 23 then the maximum value of λ+μ is
View Solution_2019_CBT8_E01_023_Q01.png)
Unpolarised light beam of intensity I0 is incident on polaroid P1. The three polaroids are arranged in such a way that transmission axis of P1 and P3 are perpendicular to each other. Angle between the trasmission axis of P2 and P3 60∘. The intensity of the beam coming out from P3 will be:
View Solution

