Fig show a double slit experiment, P and Q are the two coherent source. The path lengths PY and QY are nλ and (n+4)λ respectively where n is whole number and λ is wavelength. Taking the central bright fringe as zero, what is fromed at Y ?

First Bright
First Dark
Fourth Bright
Second Dark
The correct Answer is:C
Δx=nλ
Topper's Solved these Questions
- WAVE OPTICSBook:NARAYNAChapter:WAVE OPTICSExercise:LEVEL - III
Explore 30 Videos
- WAVE OPTICSBook:NARAYNAChapter:WAVE OPTICSExercise:NCERT Based Questions
Explore 25 Videos
- WAVE OPTICSBook:NARAYNAChapter:WAVE OPTICSExercise:LEVEL - I (C.W)
Explore 38 Videos
- SEMICONDUCTOR ELECTRONICSBook:NARAYNAChapter:SEMICONDUCTOR ELECTRONICSExercise:ADDITIONAL EXERCISE (ASSERTION AND REASON TYPE QUESTIONS :)
Explore 19 Videos
Similar Questions
In Young's double slit experiment, the distance between two coherent sources is 1 mm and the distance between the slits and the screen is 1 m. If the 10th dark fringe is at a distance of 4.75 mm from the central bright fringe, calculate
the wavelength of light used and
View SolutionIn Young's double slit experiment, the distance between two coherent sources is 1 mm and the distance between the slits and the screen is 1 m. If the 10th dark fringe is at a distance of 4.75 mm from the central bright fringe, calculate
the distance of 5th bright fringe from the central bright fringe.
View Solution
Knowledge Check
The figure shows a double slit experiment with P and Q as the slits. The path lengths PX and QX are nλ and (n+2)λ respectively, where n is a whole number and λ is the wavelength. Taking the central fringe as zero, what is formed at X?
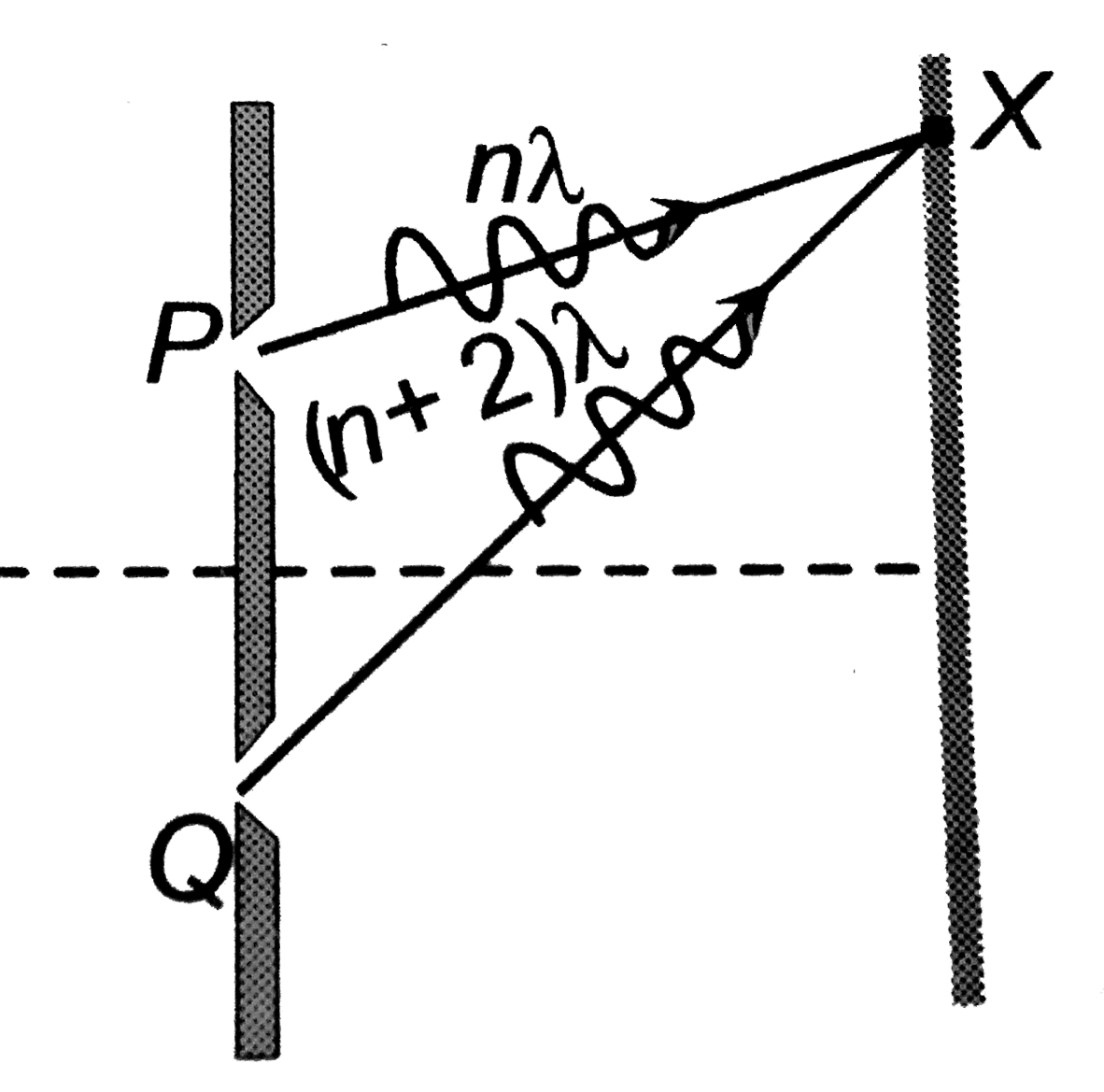 A(a) First brightB(b) First darkC(c) Second brightD(d) Second dark
A(a) First brightB(b) First darkC(c) Second brightD(d) Second darkIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is λ and I is theintensity of central bright fringe, then intensity at distance from central maximum is
AIcos2(π2xdλD)BI2sin2(πxd2λD)CIcos2(πxdλD)DIsin2(πxdλD)In young's double slit experiment sodium light composed of two wavelengths λ1 and λ2 close to each other (with λ2 greater than λ1 ) is used the order n upto which the fringes can be seen on the screen is given by
An=λ2λ2−λ1Bn=λ1λ2−λ1Cn=λ22(λ2−λ1)Dn=λ12(λ2−λ1)
In Young's double slit experiment, the two slits acts as coherent sources of equal amplitude A and wavelength λ. In another experiment with the same set up the two slits are of equal amplitude A and wavelength λ but are incoherent. The ratio of the intensity of light at the mid-point of the screen in the first case to that in the second case is
View SolutionIn a Young's double slit experiment, the slits are 2mm apart and are illuminated with a mixture of two wavelength λ0=750nm and λ=900nm. The minimum distance from the common central bright fringe on a screen 2m from the slits where a bright fringe from one interference pattern coincides with a bright fringe from the other is
View SolutionIn a Young's double slit experiment, the slits are 2mm apart and are illuminated with a mixture of two wavelength λ0=750nm and λ=900nm. The minimum distance from the common central bright fringe on a screen 2m from the slits where a bright fringe from one interference pattern coincides with a bright fringe from the other is
View SolutionIn a standard Young's double-slit experiment set-up, two point P and Q are marked on the screen Path difference corresponding to point P is λ/2 and for point Q it is λ/4. Here λ is wavelength of light being used. If IPandIQ are the resultant intensities at points P and Q, then IQ/IP is
View SolutionTwo coherent sources A & B emitting light of wavelength lambda are placed at position (-D,0) and (−D,3λ) respectively Here D >>λ The number of minima on y-axis and maxima on x-axis respectively are
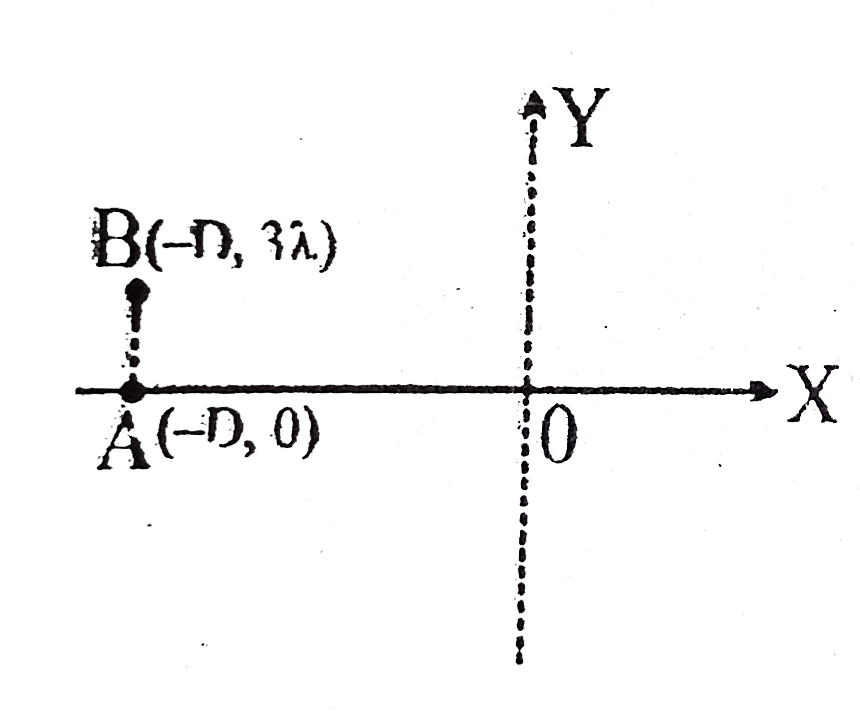
View Solution

