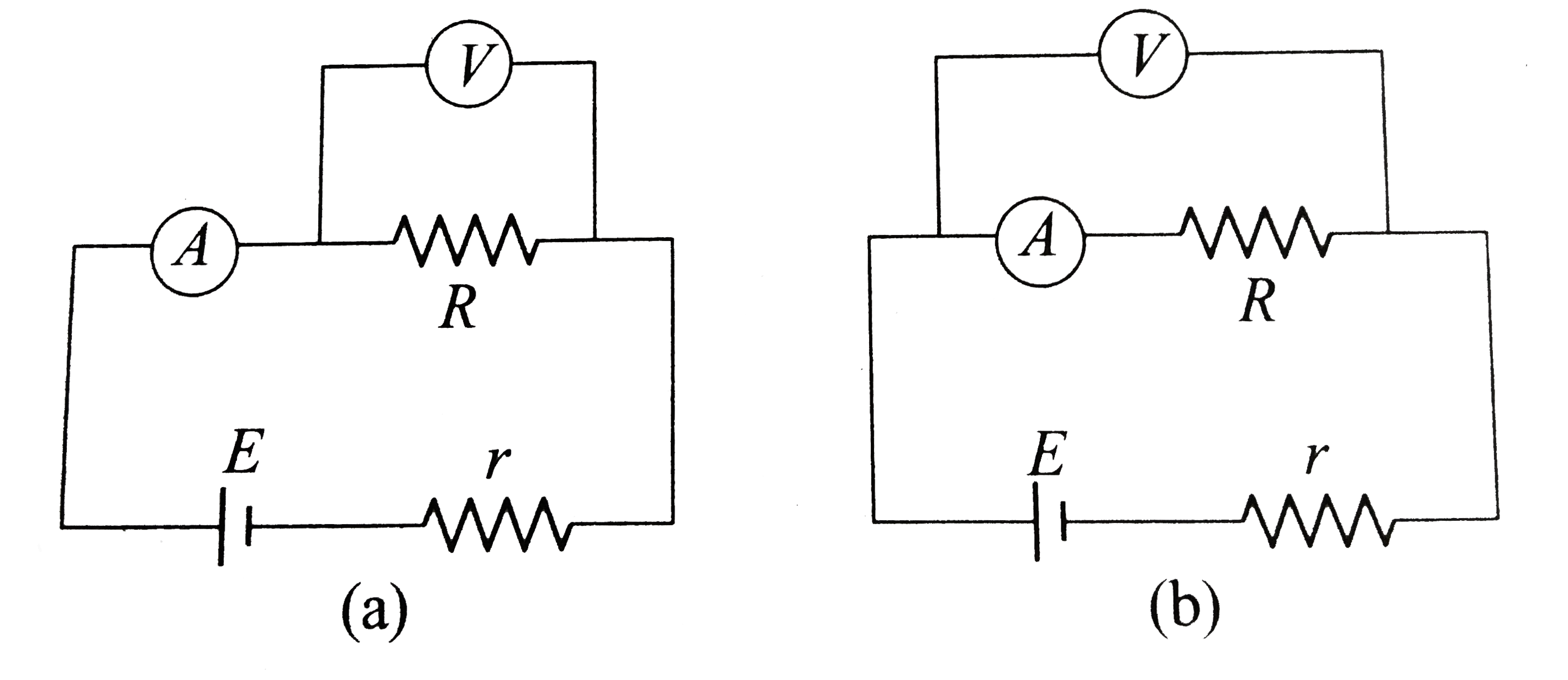
The value of resistance of an unknown resistor is calculated using the formula R=V/I where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RVandRG,respectively) are finite and nonzero.
 ,
,
Let RAandRB be the calculated values in the two cases A and B , respectively.
If the resistance of voltmeter is RV=1kΩ and the percentage error in the measurement of R (the value of R is nearly 10Ω)is
zero in both cases
non zero but equal in both cases
more in circuit A
more in circuit B
The correct Answer is:D
% error in case A
RA−RR×100=(RVR+RV−1)×100
=−RR+RV×100≈−1% % error in case B
RB−RR×100=RGR×100≈100≈10%
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - Level 6
43 Videos
- CURRENT ELECTRICITYBOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT Based Questions
13 Videos
- COMMUNICATION SYSTEMBOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)
25 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NARAYNACHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ASSERTION AND REASON
15 Videos
Similar Questions
Resistance value of an unknown resistor is calculated using the formula R=VI where V and I be the readings of the voltmeter and the ammeter respectively. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RvandRGrespectively ) are finite and non zero.

Let RvandRG be the calculated values in the two cases A and B respectively.
If the resistance of voltmeter is Rv=1kΩ and that of ammeter is RG=1Ω the magnitude of the percentage error in the measurement of R (the value of R is nearly 10Ω ) is:
View SolutionResistance value of an unknown resistor is calculated using the formula R=VI where V and I be the readings of the voltmeter and the ammeter respectively. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RvandRBrespectively ) are finite and non zero.
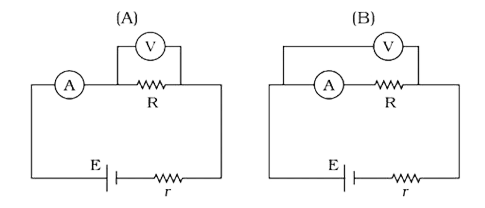
Let RAandRB be the calculated values in the two cases A and B respectively.
The relation between RA and the actual value R is
View Solution
Knowledge Check
The value of resistance of an unknown resistor is calculated using the formula R=V/I where V and I are the readings of the voltmeter and the ammeter, respectivley. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RVandRG,respectively) are finite and nonzero.
 ,
,
Let RAandRB be the calculated values in the two cases A and B , respectively.
The relation between RA and the actual value of R isAR>RABR<RACR=RBDdependent upon E and r.Let V and I be the readings of the voltmeter and the ammeter respectively as shown in the figure. Let RV and RA be their corresponding resistancce Therefore,
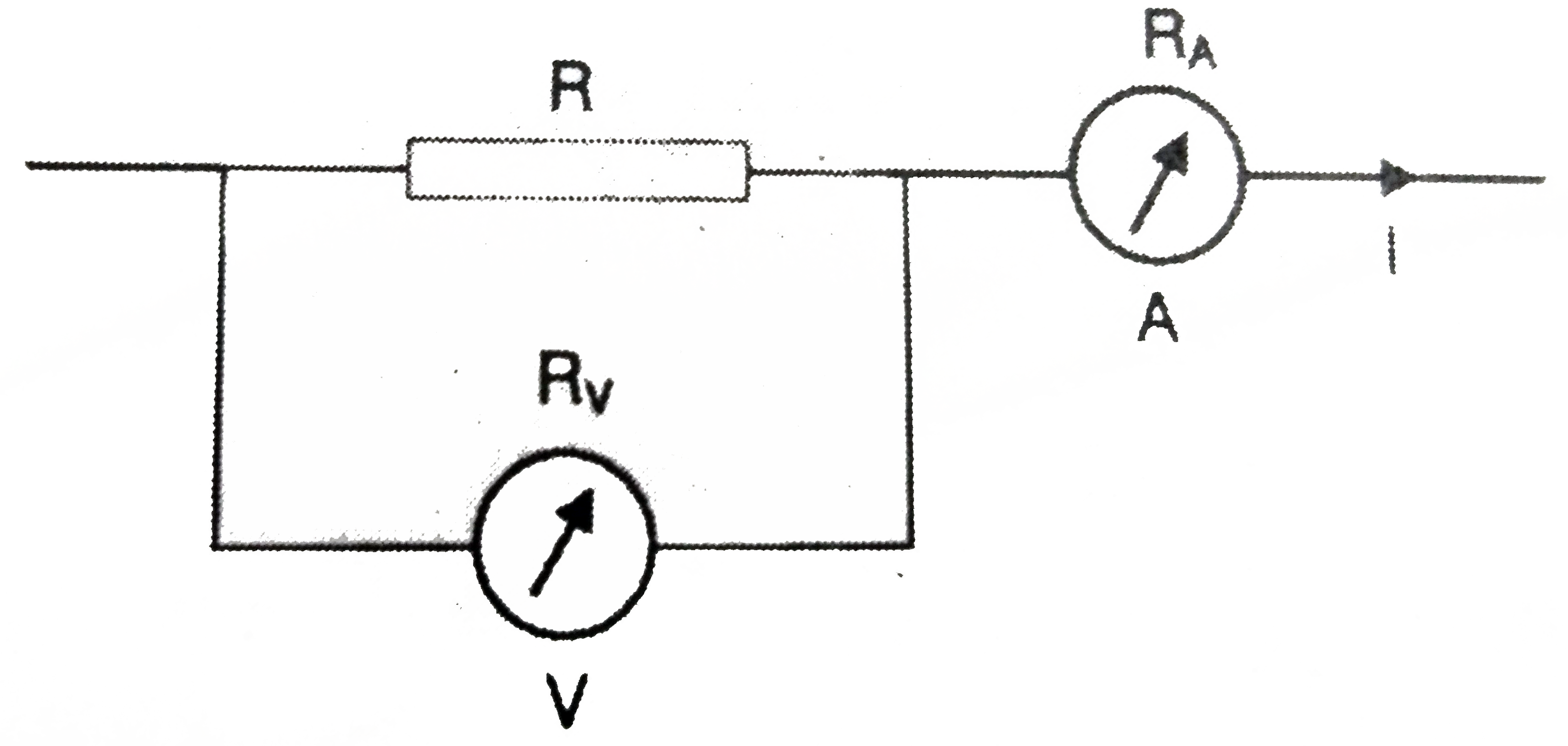 AR=VIBR=VI−(VRV)CR=RV−RADR=V(R+RA)IRA
AR=VIBR=VI−(VRV)CR=RV−RADR=V(R+RA)IRAIn the series L-C-R circuit , the voltmeter and ammeter readings are respectively
 AV = 200 V , I = 4 ABV = 150 , I = 2 ACV = 100 , I = 5 ADV = 100 V, I = 2 A
AV = 200 V , I = 4 ABV = 150 , I = 2 ACV = 100 , I = 5 ADV = 100 V, I = 2 A
Resistance value of an unknown resistor is calculated using the formula R=VI where V and I be the readings of the voltmeter and the ammeter respectively. Consider the circuits below. The internal resistances of the voltmeter and the ammeter (RvandRGrespectively ) are finite and non zero.
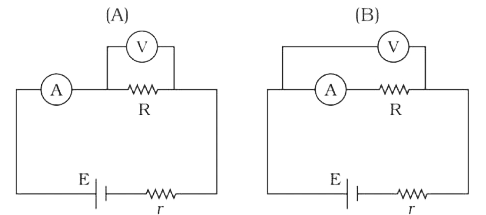
Let RvandRG be the calculated values in the two cases A and B respectively.
The relation between RBand the actual value of R is:
View SolutionThe actual value of resistance R, shown in the figure is 30Ω. This is measured in an experiment as shown using the standard formula R=VI, where V and I are the readings of the voltmeter and ammeter, respectively. If the measured value of R is 5% less, then the internal resistance of the voltmeter is
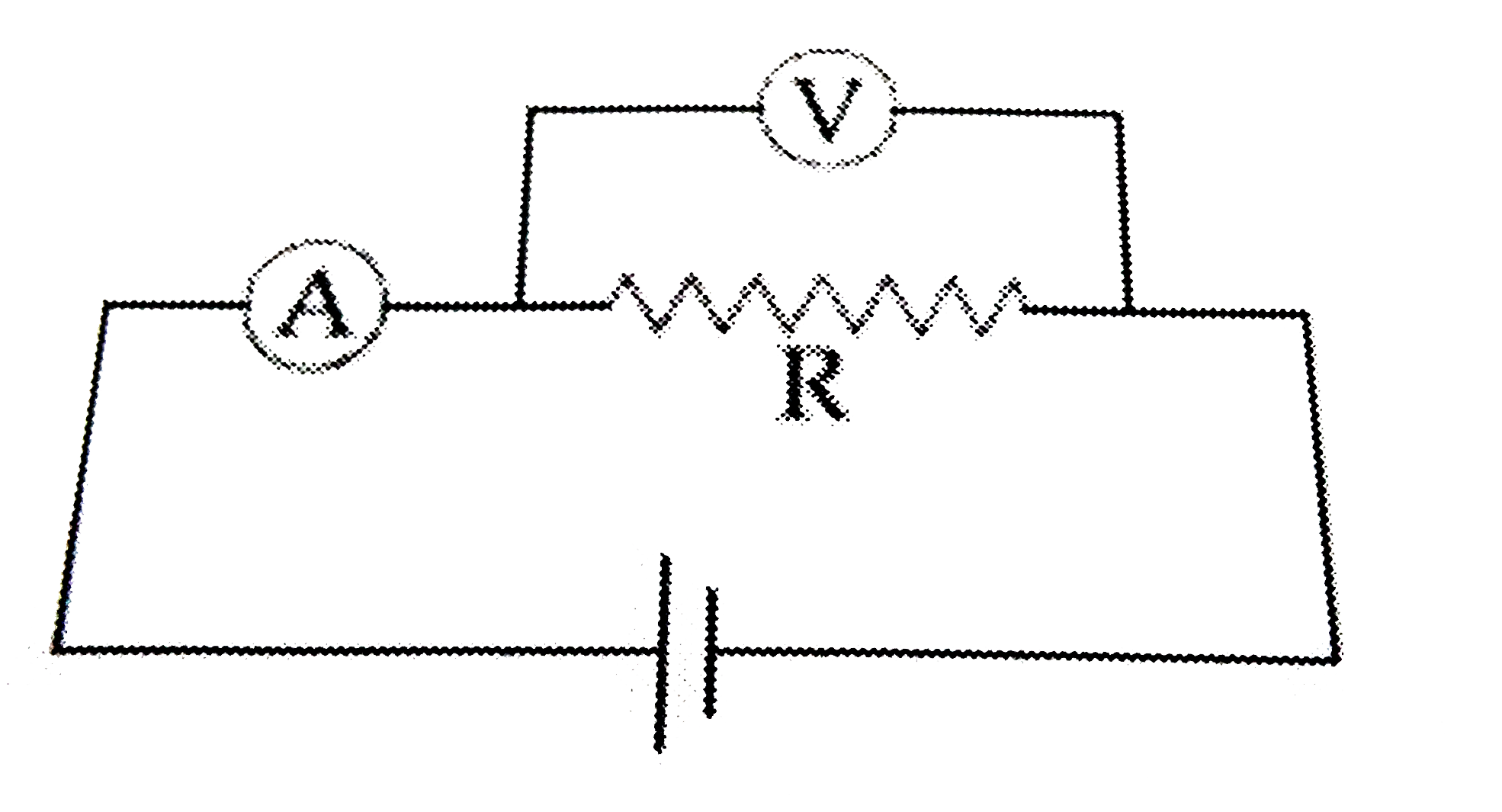
View SolutionIn the circuit shown below, the ammeter and the voltmeter readings are 3 A and 6 V respectively . Then, the value of the resistance R is
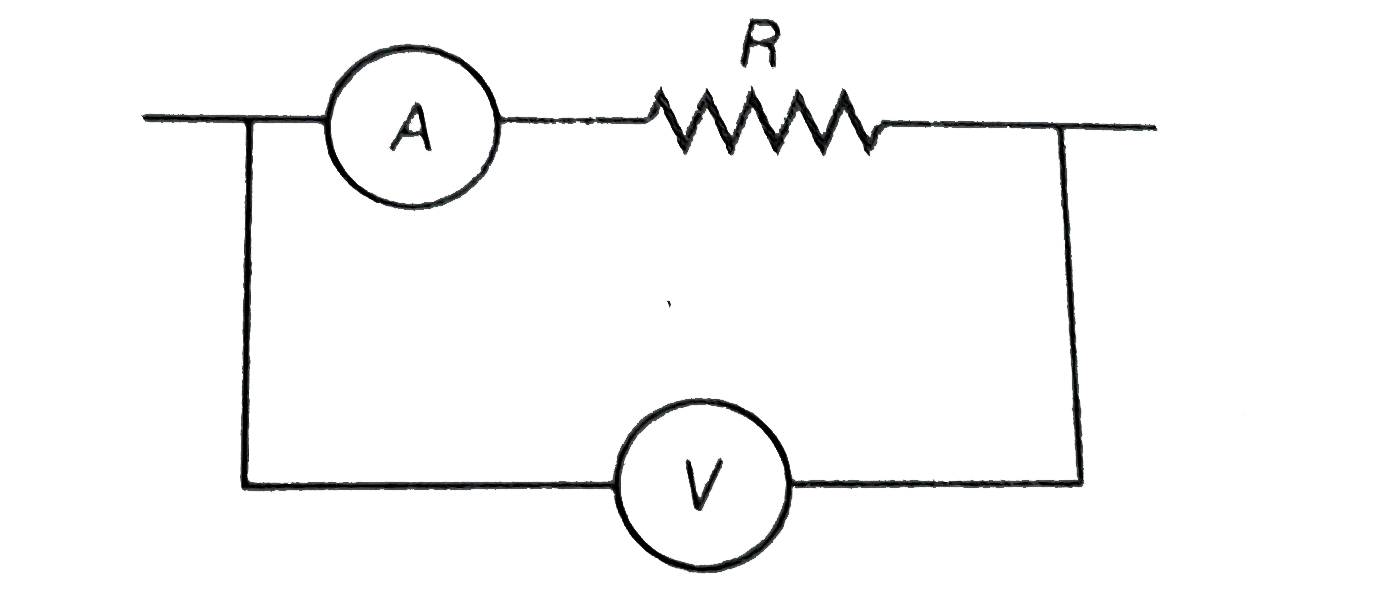
View SolutionThe ammeter A reads 2A and the voltmeter V reads 20V, the value of resistance R is (Assuming finite resistance's of ammeter and voltmeter)
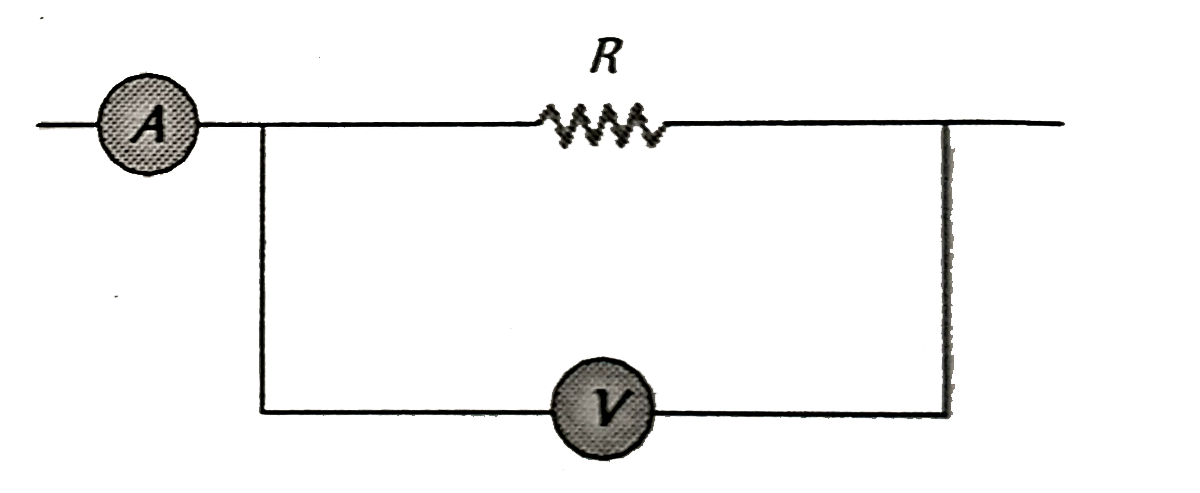
View SolutionA voltmeter and an ammeter are connected in the circuit as shown. Resistance of ammeter is say R10 and that of voltmeter is 10R. Then

View Solution
