A 4μF capacitor, a resistance of 2.5MΩ is in series with 12V battery. Find the time after which the potential difference across the capacitor is 3 times the potential difference across the resistor. [ Given In (2) = 0.693]
A
14.86s
B
6.93s
C
7s
D
14s
Video Solution
Text Solution
The correct Answer is:A
Given EC=3VR=3(V−VC)
Here V is the applied potential
∴VC=34V or E(1−e−ttc)=34V
∴e−tτc=14 Here τc=CR=10s
substituting this value of τc in Eq (i) and solving for t we get t=13.86∵
|
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - Level 6
43 Videos
- CURRENT ELECTRICITYBOOK - NARAYNACHAPTER - CURRENT ELECTRICITYEXERCISE - NCERT Based Questions
13 Videos
- COMMUNICATION SYSTEMBOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)
25 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - NARAYNACHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - ASSERTION AND REASON
15 Videos
Similar Questions
Knowledge Check
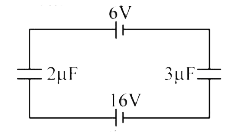
given that potential differene across 1μF capacitor is 10V. Then,
 Apotential difference across 4μF capacitor is 40VBpotential difference acros 4μF capacitor is 2.5VCpotential diference across 3μFe capacitor is 5VDvalue of E is 50V
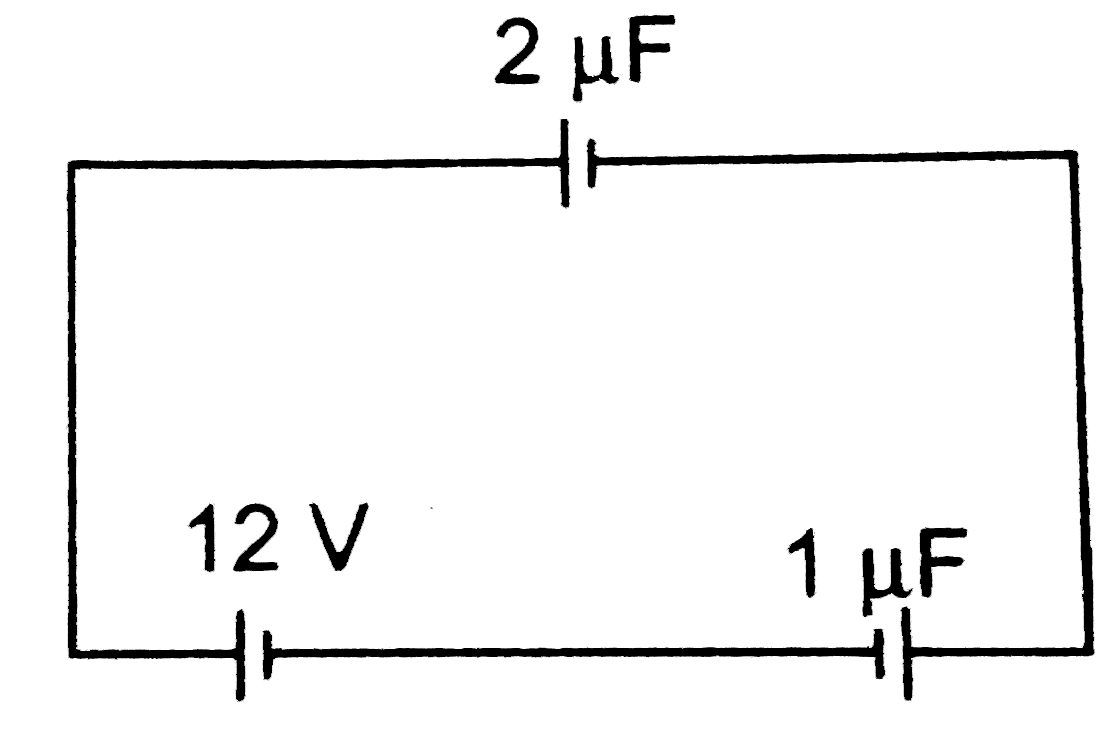
Apotential difference across 4μF capacitor is 40VBpotential difference acros 4μF capacitor is 2.5VCpotential diference across 3μFe capacitor is 5VDvalue of E is 50VIn the adjoning figure, the potential difference across the 4.5μF capacitor is
 A4 VB6 VC8 VD4.5 V
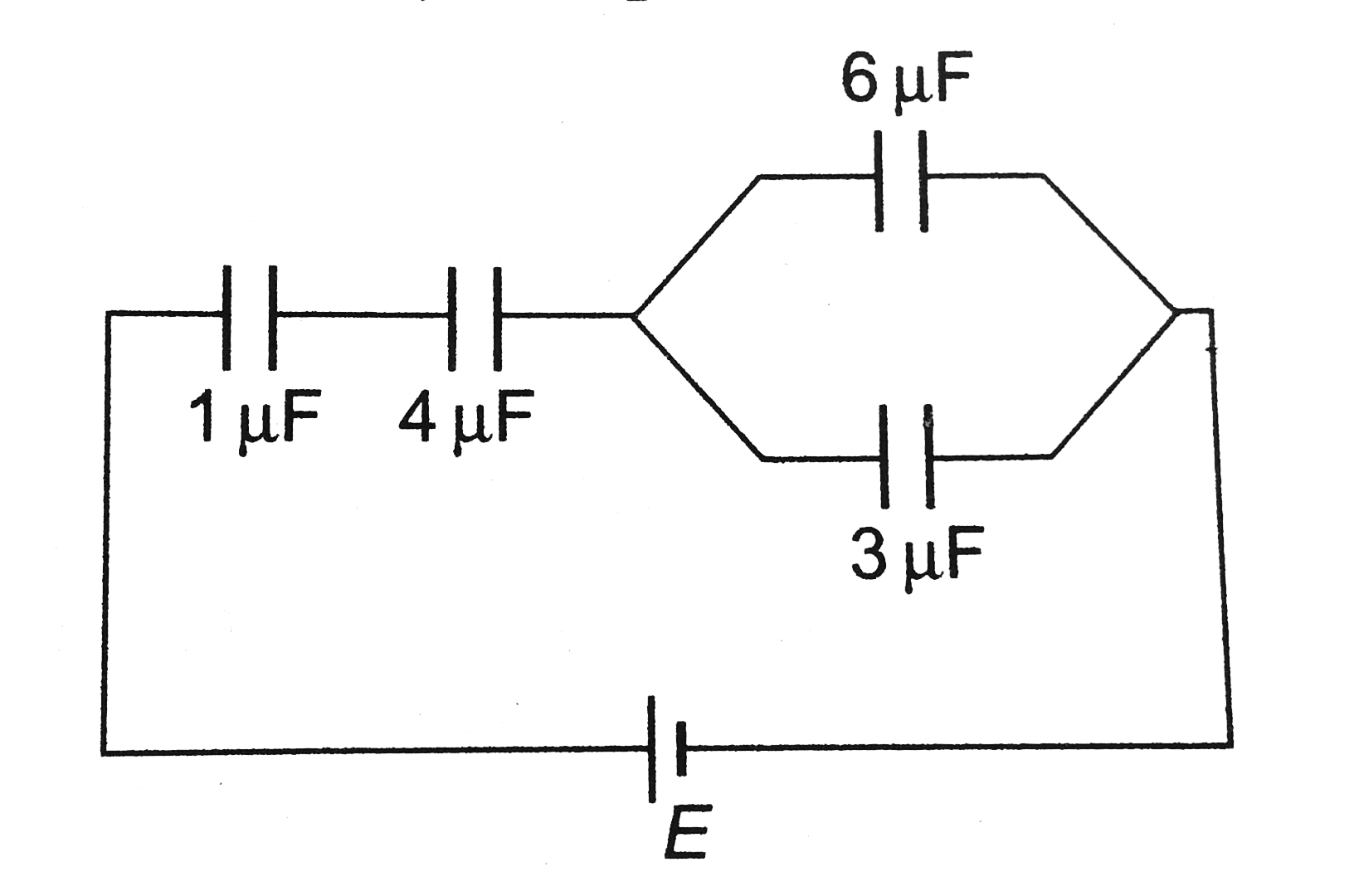
A4 VB6 VC8 VD4.5 VIn the circuit shown in the figure, the potential difference across the 4.5μF capacitor is
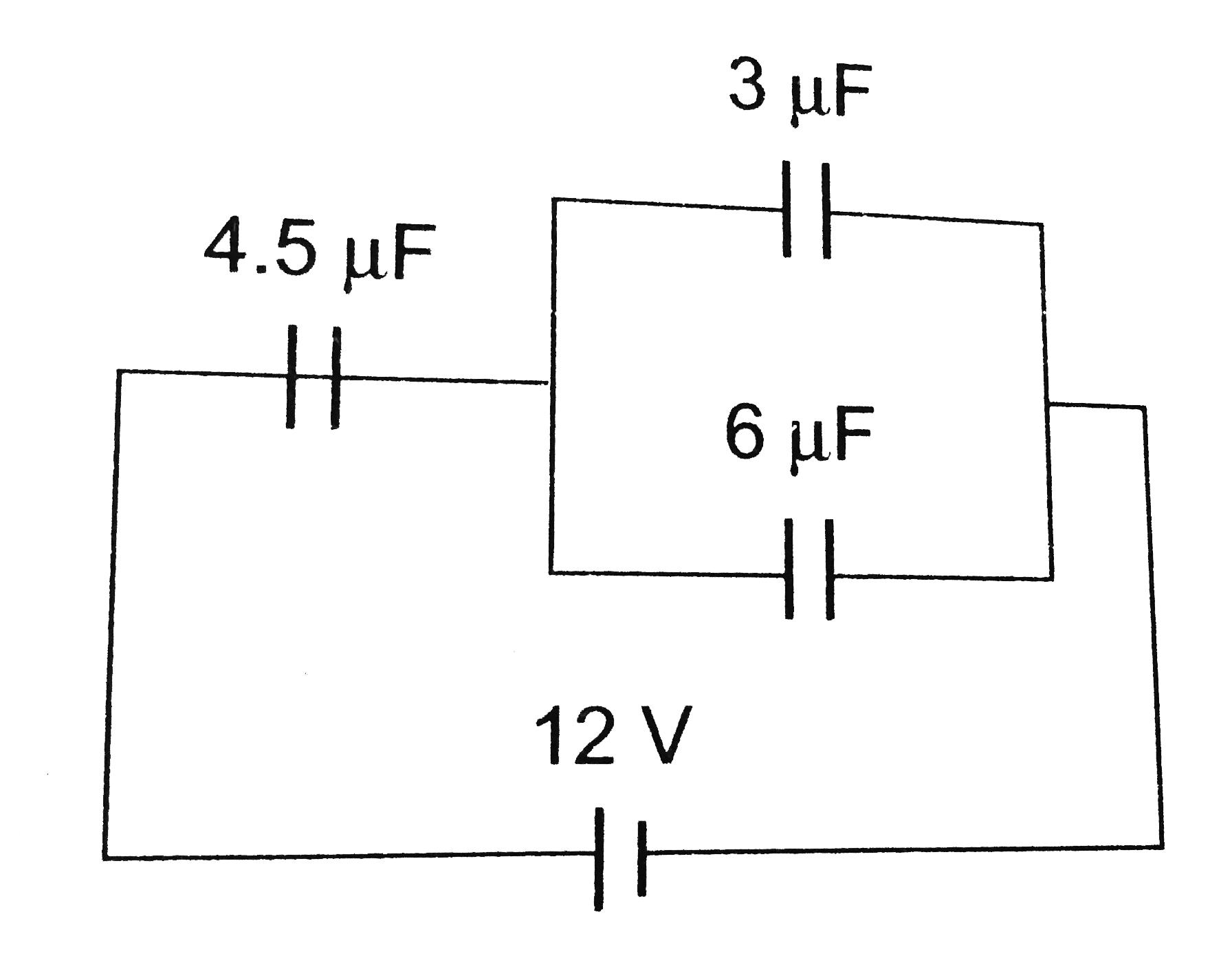 A83voltsB4 voltsC6 voltsD8 volts
A83voltsB4 voltsC6 voltsD8 volts
Find charge on each capacitor and potential difference across each capacitor .

View SolutionTwo capacitors of capacitance 6uF and 4uF are put in series across a 120V battery. What is the potential difference across the 4uF capacitor?
View SolutionIn this diagram the potential difference between A and B is 60 V. The potential difference across 6μf capacitor is
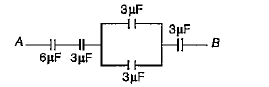
View SolutionIn the previous question, calculate the time required for the potential difference across capacitor to become equal to that across resistor.
View SolutionDuring charging of capacitor find time when potential drop across capacitor is equal to potential drop across resistance :-
View Solution