A hollow copper cylinder is of inner radius 4 cm outer radius 5 cm. Now hollow portion is completely filled with suitable copper wires. Find percentage change in its electric resistance.

Video Solution

Text Solution

Verified by Experts

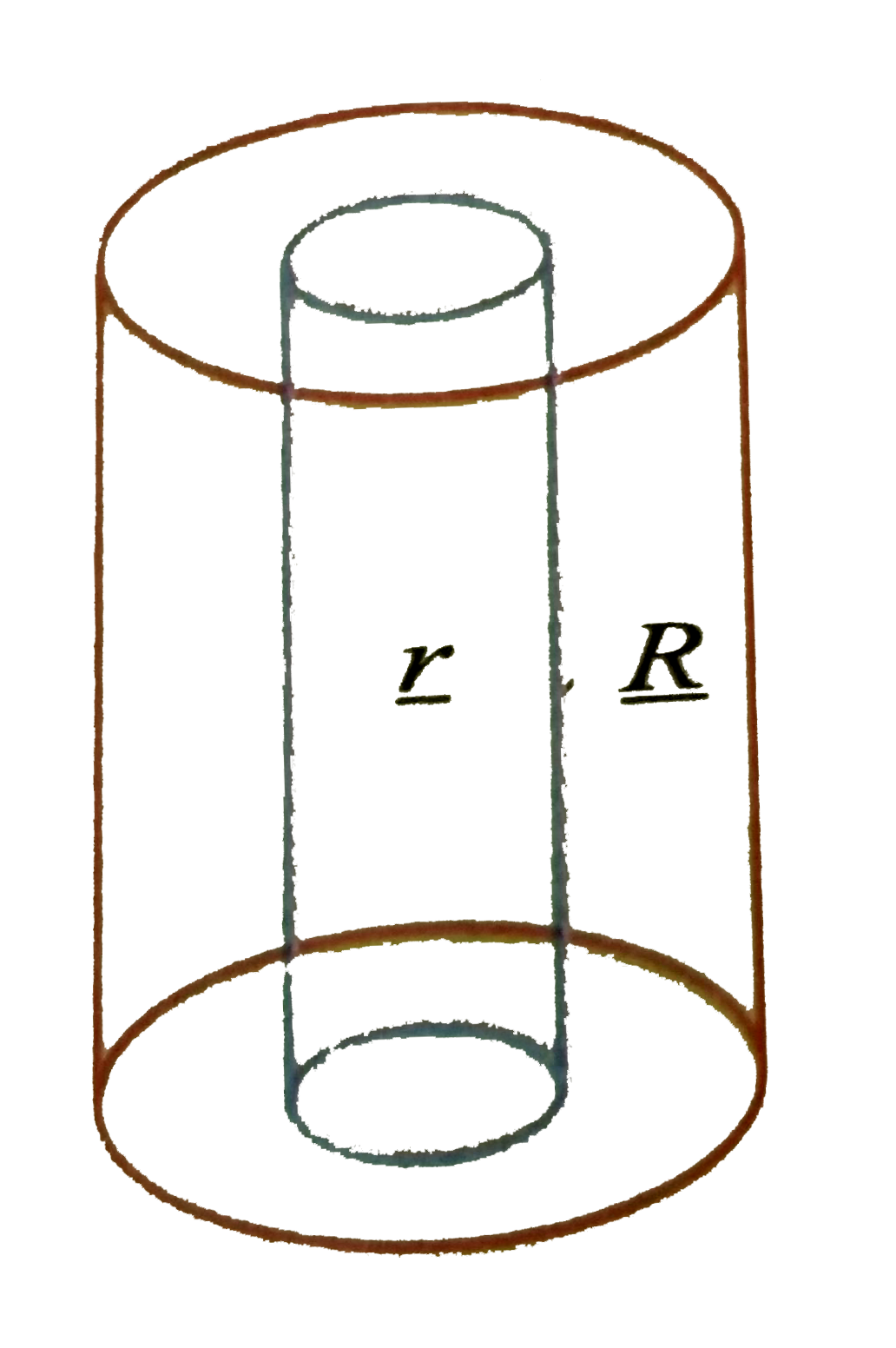
A hollow cylinder of inner radius $r$ and outer radius $R$ has specific resistance $ρ$ if its length is $l$ then its resistance
$= \frac{ρ l}{π (R^{2} - r^{2})}$
$R_{1} = \frac{ρ l}{π (5^{2} - 4^{2})} = \frac{ρ l}{9 π} = \frac{k}{9}$
Final resistance
$R_{2} = \frac{ρ l}{π (5^{2})} = \frac{ρ l}{25 π} = \frac{k}{25}$
Percentage of change $= \frac{R_{2} - R_{1}}{R_{1}} \times 100$
$= \frac{\frac{k}{25} - \frac{k}{9}}{\frac{k}{9}} \times 100 = - 64 %$

Updated on:21/07/2023

A copper cylindrical tube has inner radius $a$ and outer radius $b$ . The resistivity is $ρ$ . The resistance of the cylinder between the two ends is
A $\frac{ρ l}{b^{2} - a^{2}}$
B $\frac{ρ l}{2 π (b - a)}$
C $\frac{ρ l}{π (b^{2} - a^{2})}$
D $\frac{π (b^{2} - a^{2})}{ρ l}$
Find the volume of a hollow cylinder if its outer radius is R, inner radius is r and height is h.
A $\frac{1}{3} π (R^{2} - r^{2}) h$
B $π h (R^{2} - r^{2})$
C $π h (R^{2} + r^{2})$
D $2 π h (R - r)$
A solid sphere of copper of radius R and hollow sphere of copper of inner radius r and outer radius R are heated to the same temperature and allowed to cool in the same environment. The rate of cooling is
Amore for hollow sphere
Bmore for solid sphere
Csame for both the sphere
Dcan not say