Question

Three small bodies with the mass ratio 3 : 4: 5 (the mass of the lightest body is m) are kept at three different points on the inner surface of a smooth hemispherical cup of radius r. The cup is fixed at its lowest point on a horizontal surface. At a certain instant, the bodies are released. Determine the maximum amount of heat Q that can be liberated in such a system.At what initial arrangement of the bodies will the amount of liberated heat be maximum ? Assume that collisions are perfectly inelastic.

Options

A. `2 mgr`
B. `3 mgr`
C. `6 mgr`
D. `4 mgr`

Answer

D

Explanation

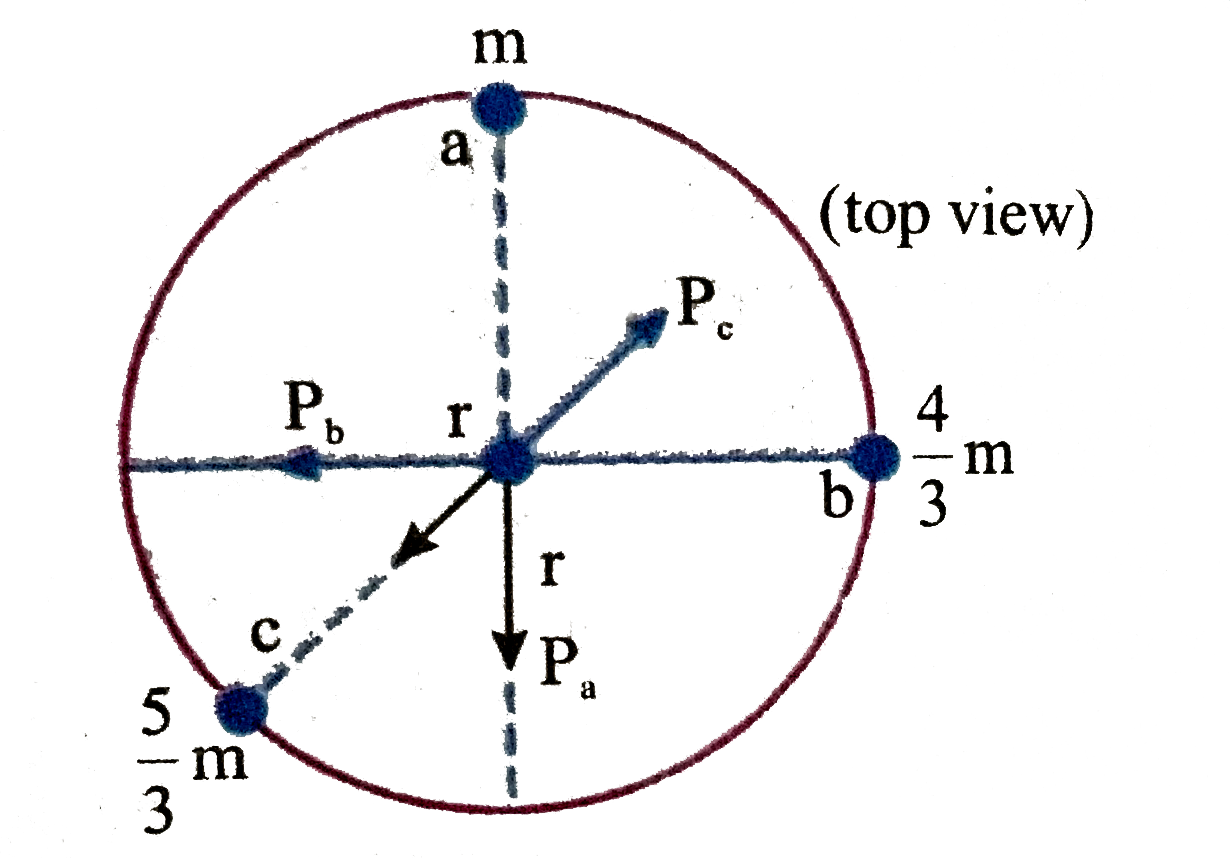
For the liberated amount of heat to be maximum the following conditions must be satisfied.
1) The potential energy of the bodies must be maximum at the intial moment
2)The bodies must collide simultaneously at the lowest point of the cup.
3) The velocity of the bodies must be zero immediately after the collision.
4) If these conditions are statisfied the whole of the initial `P.E`. of the bodies will be transformed into heat.
After the bodies are left to themselves the amount of heat `'Q'` liberated in the system is maximum and eaul to `4 mgr`.
`P.E` before collision`=` Heat
`=mgr+(4)/(3)mgr+(5)/(3)mgr=(3mgr+4mgr+5mgr)/(3)=(12mgr)/(3)=4mgr`
`v_(2) cos phi=(300)/(4)`.....(1)