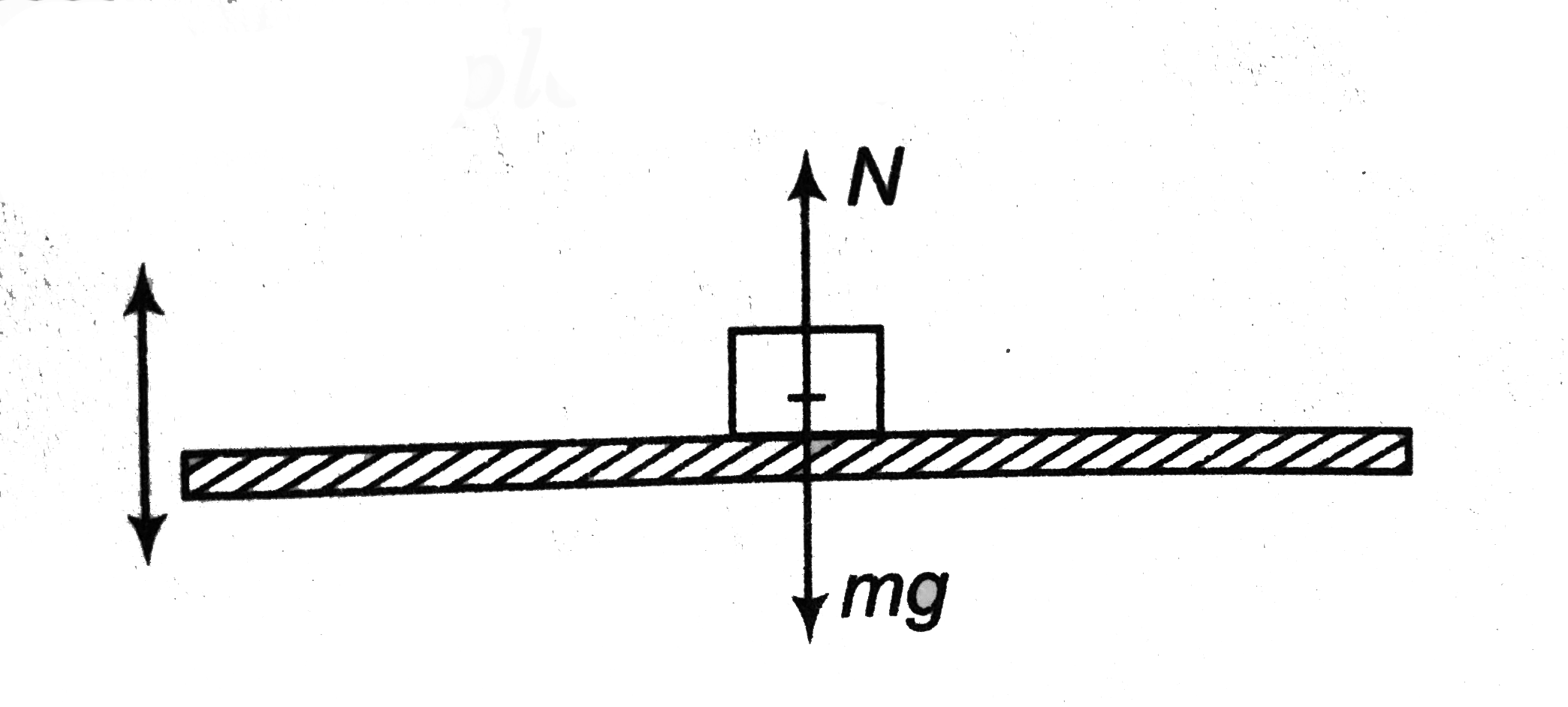
A block of 0.5kg is placed on a horizontal platform. The system is making vertical oscillations about a fixed point with a frequency of 0.5Hz. The maximum displacement of oscillation, if the block does not lose contact with the horizontal platform is nearly
0.5m
0.75m
1m
1.2m
The correct Answer is:C
mg=FSHM+N,mg=mω2A+0(∵N=0)
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - DAMPED OSCILLATIONS
1 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - ILLUSTRATION
37 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-II (H.W)
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
A block is kept is kept over a horizontal platform, executing vertical SHM of angular frequency ω. Find maximum amplitude of oscillations, so that the block does not leave contact with the platform.
View SolutionA coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time :
View Solution
Knowledge Check
A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time :
Aat the highest position of the platformBat the mean position of the platformCfor an amplitude of gω2Dfor an amplitude of g2ω2A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
A(a) at the mean position of the platformB(b) for an amplitude of gω2C(c) for an amplitude of g2ω2D(d) at the highest position of the platformA horizontal platform is undergoing vertical S.H>M of time period T. A block of mass M is placed on the platform . The maximum mplitude of the platform so that the block is not detached form it is
AgT22π⋅2BgT24π2C2gT22π2D4gT2π2
A coin is placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency ω. The amplitude of oscillation is gradually increased. The coin will leave contact with the platform for the first time
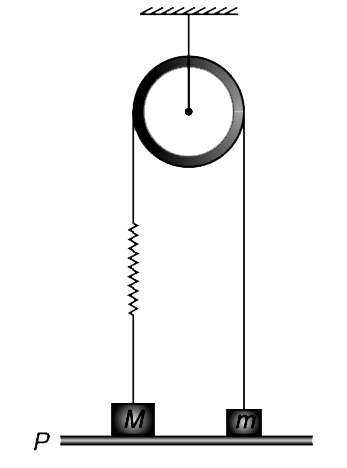
View SolutionIn the arrangement shown in the fig. the pulley, the spring and the thread are ideal. The spring is stretched and the two blocks are in contact with a horizontal platform P. When the platform is gradually moved up by 2 cm the tension in the string becomes zero. If the platform is gradually moved down by 2 cm from its original position one of the blocks lose contact with the platform. Given M = 4 kg, m = 2 kg.
(a) Find the force constant (k) of the spring
(b) If the platform continues to move down after one of the blocks loses contact, will the other block also lose contact? Assume that that the platform moves very slowly.
View SolutionA block is kept on a horizontal table. The table is undergoing simple farmonic motion of frequency 3Hz in a horizontal plane. The coefficient of static friction between the block and the table surface is 0.72. find the maximum amplitude of the table at which the block does not slip on the surface g=10ms−1
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA spring - block system undergoes vertical oscillation above a large horizontal metal sheet with uniform positive charge. The time period of the oscillation will be is given a charge Q , its time period of oscillation will be
View Solution
