A force of 4 dynes is present on a particle of mass 4g on X-axis. If it is at rest at x=10cm initially, the equation for its motion is
(d2xdt2)+x=0
(dxdt)2+x=0
(d2xdt2)+16x=0
(dxdt)2+16x=0
The correct Answer is:A
F=−4x,ma=−4x,⇒d2xdt2+ω2x=0
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:DAMPED OSCILLATIONS
Explore 1 Video
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:ILLUSTRATION
Explore 37 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL-II (H.W)
Explore 1 Video
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
A force F=−10x+2 acts on a particle of mass 0.1kg where x is in m and F in newton. If is released from rest at x=0, find:
a. Amplitude:
b. Time period:
c. Equation of motion.
View SolutionThe figure shows the force (F) versus displacement (s) graph for a particle of mass m=2kg initially at rest.
(i) The maximum speed of the particle occurs at x = …..m
(ii) The maximum speed of the particle is ….ms−1
(iii) The particle once again has its speed zero at x =....m
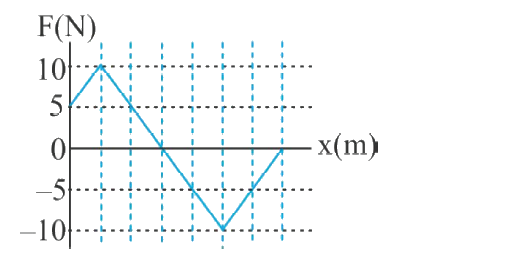
View Solution
Knowledge Check
A force of 50 dynes is acted on a body of mass 5 g which is at rest for an interval of 3 seconds, then impulse is
A0.15×10−3N-sB0.98×10−3N-sC1.5×10−3 N-sD2.5×10−3 N-sA force of 50 dynes is acted on a body of mass 5 g which is at rest for an interval of 3 seconds, then impulse is
A0.15×10−3 NsB0.98×10−3 NsC1.5×10−3 NsD2.5×10−3 NsThe potential energy in joules of a particle of mass 1 kg moving in a plane is given by U=3x+4y, the position coordinates of the point being x and y, measured in metres. If the particle is initially at rest at (6, 4), then:
Aits acceleration is of magnitude 5m/s2Bits speed when it crosses they-axis is 10m/sCit crosses the y-axis (x=0) at y=−4Dit moves in a straight line passing through the origin (0, O)
A force fo 3000 dyne acts on a body of mass 400g for 10s. Find the kinetic energy of the body after 10s.
View SolutionA time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m/s along negative x-axis at time t=0. Find the velocity of the particle at the end of 4s.
View SolutionA particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View SolutionA particle of mass 4g is in a gravitational potential V=(800x2+150)erg/g. Its frequency of oscillation is
View SolutionA particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
View Solution

