For a bar pendulum the distance between two points of minimum time period is
equal to the radius of gyration
twice the radius of gyration
twice the length of an equivalent simple pendulum
twice the length fo a compound pendulum
The correct Answer is:B
Step by step video, text & image solution for For a bar pendulum the distance between two points of minimum time period is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL -I (C.W)
Explore 34 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL -II (C.W)
Explore 36 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - IV
Explore 41 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
A hollow sphere field with water is used as the bob of a pendulum. Assume that the equation for simple pendulum is valid with the distance between the point of suspension and centre of mass of the bob acting as the effective length of the pendulum. If water slowly leaks out of the bob, how will the time period vary?
View SolutionA simple pendulum is moving simple harmonically with a period of 6 s between two extreme positions B and C about a point O. If the distance between B and C is 10 cm, then the time taken by the pendulum to move from position C to position D exactly midway between O and C will be
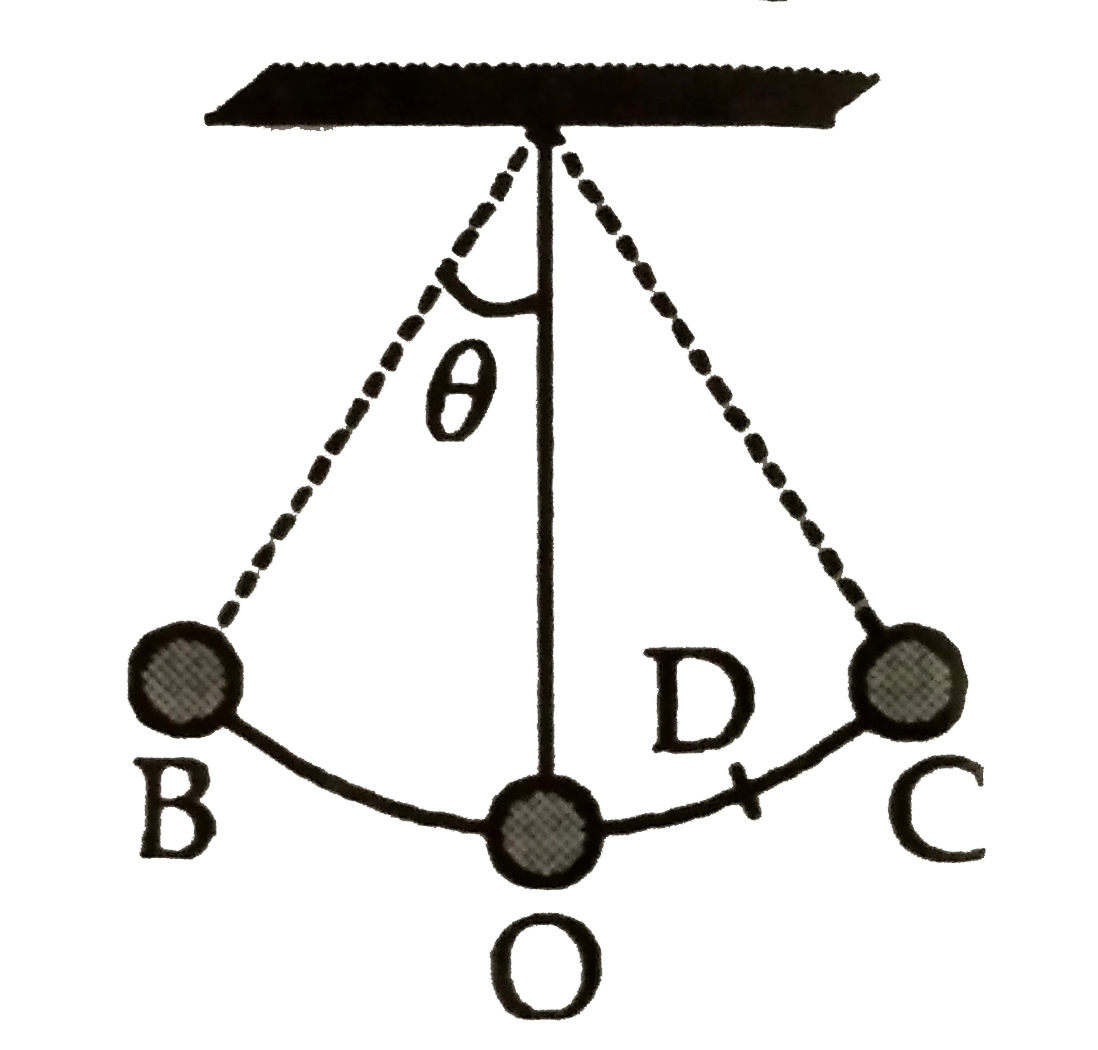
View Solution
Knowledge Check
The minimum distance between the two points having the same phase is
Awavelength of the waveBamplitude of the waveCwave numberDfrequency of the waveFor a simple pendulum the graph between length and time period will be
AhyperbolaBparabolaCstraight lineDnone of theseAssertion :- For a physical pendulum if distance of point of suspension from centre of mass increases time period first decreases then increases.
Reason :- For a physical pendulum there is some distance from centre of mass at which frequency of oscillation is maximum.AIf both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.BIf both Assertion & Reason are True but Reason is not a correct explanation of the Assertion.CIf Assertion is True but the Reason is False.DIf both Assertion & Reason are False.
If a pendulum is allowed to oscillate in vacuum, its time period will
View SolutionSimple pendulum is executing simple harmonic motion with time period T. If the length of the pendulum is increased by 21%, then the increase in the time period of the pendulum of the increased length is:
View SolutionFor a compound pendulum, the maximum time period is :
View SolutionFor a given length of a pendulum, the time period is maximum
View SolutionThe distance of point of a compound pendulum form its centre of gravity is l, the time period of oscillation relative to this point T. If g=π2, the relation between l and T will be :-
View Solution