An alternating emf given by V=V0sinωt has peak value 10 volt and freguency 50 Hz The instantaneous emf at .
10V
5√3V
5V
1V
The correct Answer is:C
To find the instantaneous emf given by the equation V=V0sin(ωt), we will follow these steps:
Step 1: Identify the given values
- Peak value V0=10 volts
- Frequency f=50 Hz
Step 2: Calculate the angular frequency ω
The angular frequency ω is given by the formula:
ω=2πf
Substituting the given frequency:
ω=2π×50=100πrad/s
Step 3: Write the equation for instantaneous emf
The equation for instantaneous emf is:
V(t)=V0sin(ωt)
Substituting the values of V0 and ω:
V(t)=10sin(100πt)
Step 4: Substitute t=1600 seconds into the equation
Now, we will substitute t=1600 seconds into the equation:
V(1600)=10sin(100π×1600)
Step 5: Simplify the argument of the sine function
Calculating the argument:
100π×1600=100π600=π6
Thus, we have:
V(1600)=10sin(π6)
Step 6: Calculate the sine value
The sine of π6 is:
sin(π6)=12
Step 7: Calculate the instantaneous emf
Substituting the sine value back into the equation:
V(1600)=10×12=5volts
Final Answer
The instantaneous emf at t=1600 seconds is 5 volts.
---
- Peak value V0=10 volts
- Frequency f=50 Hz
The angular frequency ω is given by the formula:
ω=2πf
Substituting the given frequency:
ω=2π×50=100πrad/s
The equation for instantaneous emf is:
V(t)=V0sin(ωt)
Substituting the values of V0 and ω:
V(t)=10sin(100πt)
Now, we will substitute t=1600 seconds into the equation:
V(1600)=10sin(100π×1600)
Calculating the argument:
100π×1600=100π600=π6
Thus, we have:
V(1600)=10sin(π6)
The sine of π6 is:
sin(π6)=12
Substituting the sine value back into the equation:
V(1600)=10×12=5volts
The instantaneous emf at t=1600 seconds is 5 volts.
Topper's Solved these Questions
Similar Questions
.The peak value of an alternating e.m.f. which is given by E=E_(0) coswt is 10 volts and its frequency is 50Hz .At time t=(1)/(600) s,the instantaneous e.m.f.is
View SolutionAn alternating voltage V=V0sinωt is applied across a circuit. As a result, a current I=I0sin(ωt–p2) flows in it. The power consumed per cycle is
View Solution
Knowledge Check
The peak value of an alternating emf E given by
E=(E0)cosωt
is 10V and freqency is 50 Hz. At time t=(1/600)s the instantaneous value of emf isA10VB5√3VC5VD1 VAn alternating e.m.f. is given by E=10cosωt. If the frequency is 50 Hz, then at time t=(1600)s the instantaneous value of e.m.f. is
A5 voltB1 voltC10 voltD5√3 voltThe rms value of the emf given by E=8sinωt+6sin2ωt .
A5√2VB7√2VC10VD10√2V
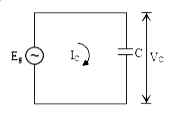
In a circuit consisting of a capacitance and a generator with alternating emf Eg=Eg0sinωt, V_CandI_C are the voltage and current. Correct phasor diagram for such circuit is :
View SolutionIn an AC circuit, voltage V = V0sinωt and inductor L is connected across the circuit. Then the instantaneous power will be
View SolutionAn alternating emf, e=200 sin ωt is applied to a lamp, whose filament has a resistance of 1000Ω. The rms valve of current is
View SolutionAn alternating emf given by equation
e=300sin(100π)tV
is applied to a resistance 100Ω. The rms current through the circuit is (in amperes).
View SolutionThe alternating emf of e=e0 sin ωt is applied across capacitor C. the current through the circuit is given by
View Solution

