The heat produced in a given resistor in a given time by the sinusoidal current I0 sin ωt will be the same as that by a steady current of magnitude .
I0√2
I0
I0√2
I02
The correct Answer is:A
To solve the problem, we need to find the steady current (DC) that produces the same amount of heat in a resistor as the sinusoidal alternating current (AC) given by I0sin(ωt).
1. Understanding Heat Produced in a Resistor:
The heat produced in a resistor due to a current is given by the formula:
H=I2Rt
where H is the heat produced, I is the current, R is the resistance, and t is the time.
2. Heat Produced by AC Current:
For the sinusoidal current I(t)=I0sin(ωt), we need to calculate the average current over a complete cycle. The effective (RMS) value of the sinusoidal current is given by:
Irms=I0√2
3. Calculating Heat Produced by AC:
The heat produced by the AC current over time t can be expressed as:
HAC=(Irms)2Rt=(I0√2)2Rt=I202Rt
4. Heat Produced by Steady Current (DC):
Let the steady current (DC) that produces the same heat be I. The heat produced by this steady current over the same time t is:
HDC=I2Rt
5. Equating Heat Produced by AC and DC:
Since the heat produced by both currents is the same, we can set the equations equal to each other:
HAC=HDC
This gives us:
I202Rt=I2Rt
6. Simplifying the Equation:
We can cancel R and t from both sides (assuming they are non-zero):
I202=I2
7. Solving for Steady Current I:
Taking the square root of both sides, we find:
I=I0√2
Final Answer:
The magnitude of the steady current I that produces the same heat as the sinusoidal current I0sin(ωt) is:
I=I0√2
The heat produced in a resistor due to a current is given by the formula:
H=I2Rt
where H is the heat produced, I is the current, R is the resistance, and t is the time.
For the sinusoidal current I(t)=I0sin(ωt), we need to calculate the average current over a complete cycle. The effective (RMS) value of the sinusoidal current is given by:
Irms=I0√2
The heat produced by the AC current over time t can be expressed as:
HAC=(Irms)2Rt=(I0√2)2Rt=I202Rt
Let the steady current (DC) that produces the same heat be I. The heat produced by this steady current over the same time t is:
HDC=I2Rt
Since the heat produced by both currents is the same, we can set the equations equal to each other:
HAC=HDC
This gives us:
I202Rt=I2Rt
We can cancel R and t from both sides (assuming they are non-zero):
I202=I2
Taking the square root of both sides, we find:
I=I0√2
The magnitude of the steady current I that produces the same heat as the sinusoidal current I0sin(ωt) is:
I=I0√2
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure the steady state current is
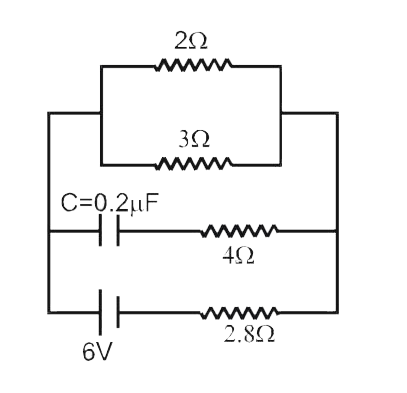 AzeroB0.6AC0.9AD1.5A
AzeroB0.6AC0.9AD1.5AThe heat produced in a wire of resistance 'x' when a current 'y' flows through it in time 'z' is given by:
Ax2×y×zBx×z×y2Cy×z2×xDy×z×xThe total heat produced in resistor r in an RL circuit when the current in the inductor decreases from Io to 0 is
ALI20B12LI20C32LI20D13LI20
In the given circuit diagram , current in 2Ω resistor is 2 A , then the current in 6Ω resistor Will be
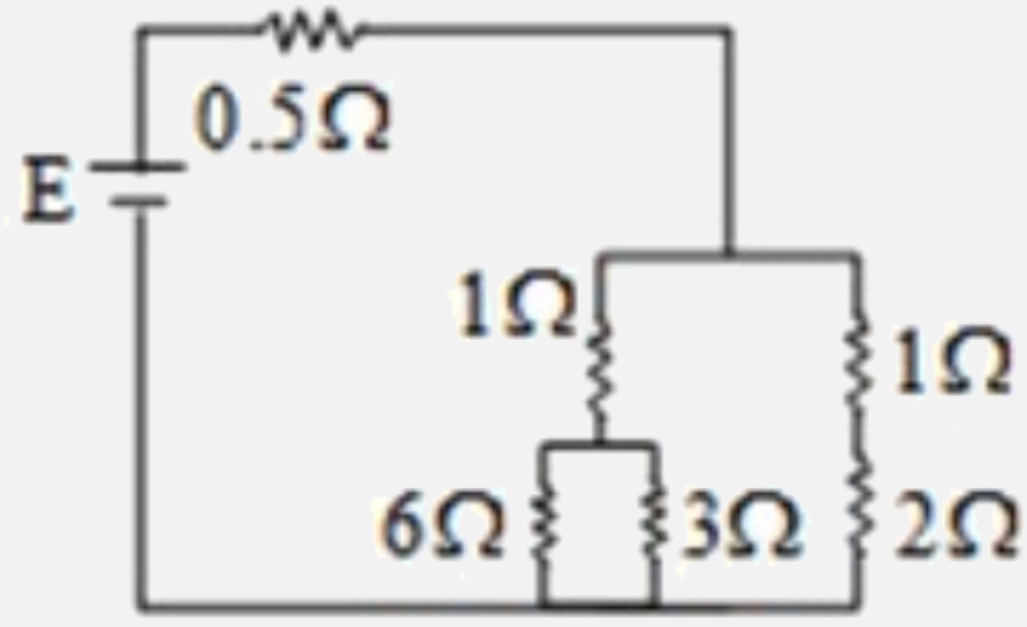
View SolutionThe average value of alternating current I=I0sinωt in time interval [0,πω] is
View SolutionThe heat produced (in calories) in a resistance R when a current I amperes flows through it for t seconds is given by the expression
View SolutionThe power dissipated in alternating circuit with voltage e=e0 sin ωt and current I=I0sin(ωt−ϕ) is
View SolutionAn alternating current is given by
(√3sinωt+cosωt). The rms current is :
View Solution


