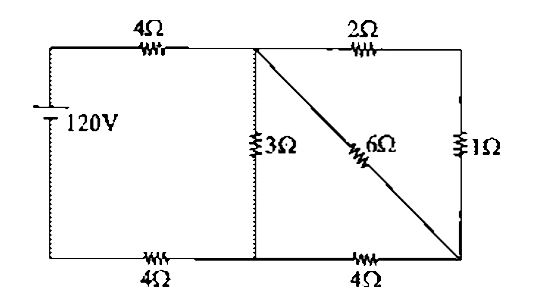
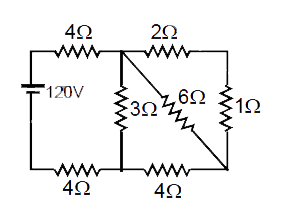find
(a) the current in 3Ω resistance
(b) the change on the capacitor

Video Solution
Text Solution

Loop 1, A to Apath ACBA
VA=(i−i1)×4+4+4i1=VA
−4i+4i1+4+4i1=VA
i−2i1=1 ..(i)
loop 2, A to A , path ABYXA
VA−i1×4−I×3−i×1+8=VA
−4i1−3i−i+8=0
4i+4i1=8
i+i1=2..(ii)
Solving
i=53A,i1=13A
(b) Branch XMY
VX−VY=8−i×1=8−53×1=193V
Branch XLY:
VX+3−V0=VY
V0=VX−VY+3=193+3=283V
Charge on capacitor Q=6V0=6×283=56μC.
|
Topper's Solved these Questions
- THERMAL AND ELECTRIC EFFECT oF CURRENTBook:CP SINGHChapter:THERMAL AND ELECTRIC EFFECT oF CURRENTExercise:Exercises
Explore 101 Videos
- SEMICONDUCTORSBook:CP SINGHChapter:SEMICONDUCTORSExercise:Exercises
Explore 140 Videos
- WAVE NATURE OF LIGHTBook:CP SINGHChapter:WAVE NATURE OF LIGHTExercise:EXERCISES
Explore 140 Videos
Similar Questions
Knowledge Check
Current in 3Ω resistance is
 A1AB17AC57AD157A
A1AB17AC57AD157AThe current in 1Ω resistance and charge stored in the capacitor are
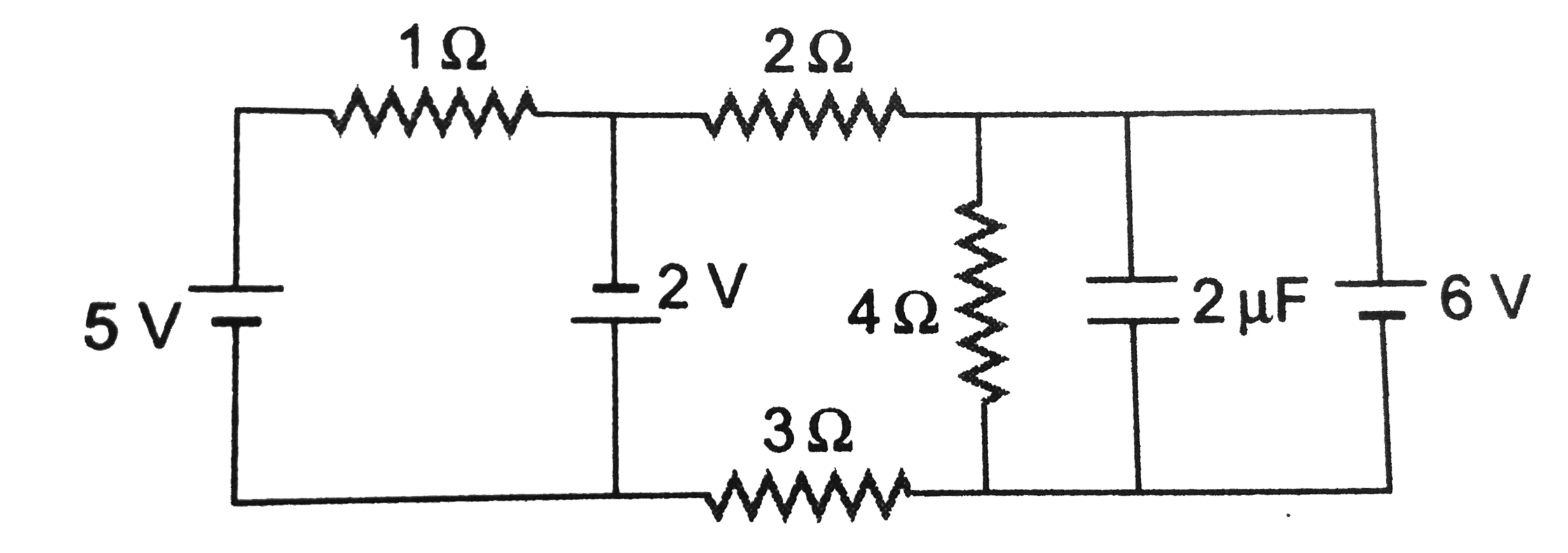 A4A,6μCB7A,12μCC4,12μCD7A,6μC
A4A,6μCB7A,12μCC4,12μCD7A,6μCIn the circuit shown, the current in 3Ω resistance is
 A1AB17AC57AD157A
A1AB17AC57AD157A
The current flowing in 3Ω Resistance will be
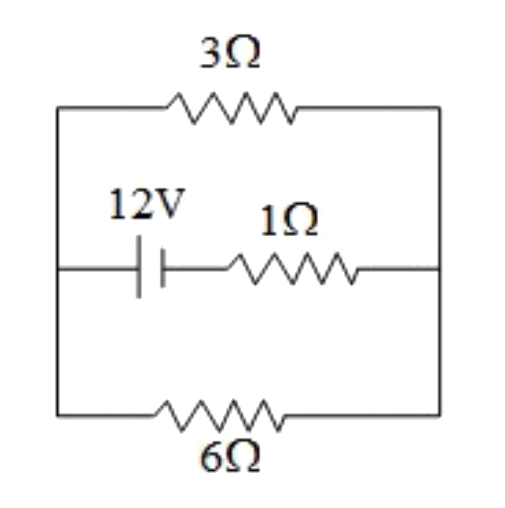
View SolutionIn the circuit shown in figure-3.355, the current in 1Ω. resistance and charge stored in the capacitor are
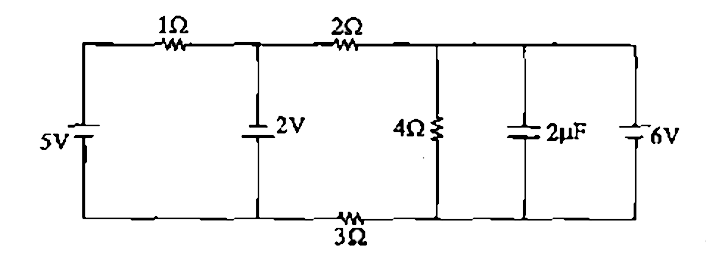
View SolutionIn the circuit shown in figure-3.166 the cells are ideal Calculate(a) The current in 3Ω resistance (b) Current the cell the 8V cell and (c) The steady state charge on the capacitor.
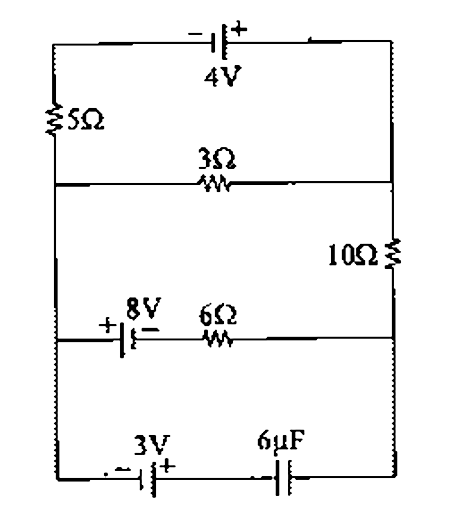
View SolutionIn the circuit shown in figure-3.238, find the current in 6Ω resistance just after closing the switch S.
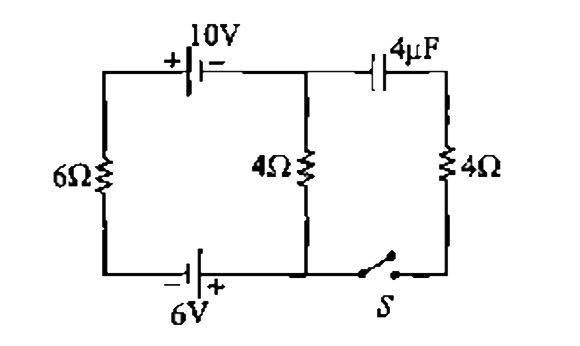
View SolutionFind the current through 23Ω resistance in the figure shown.
View Solution