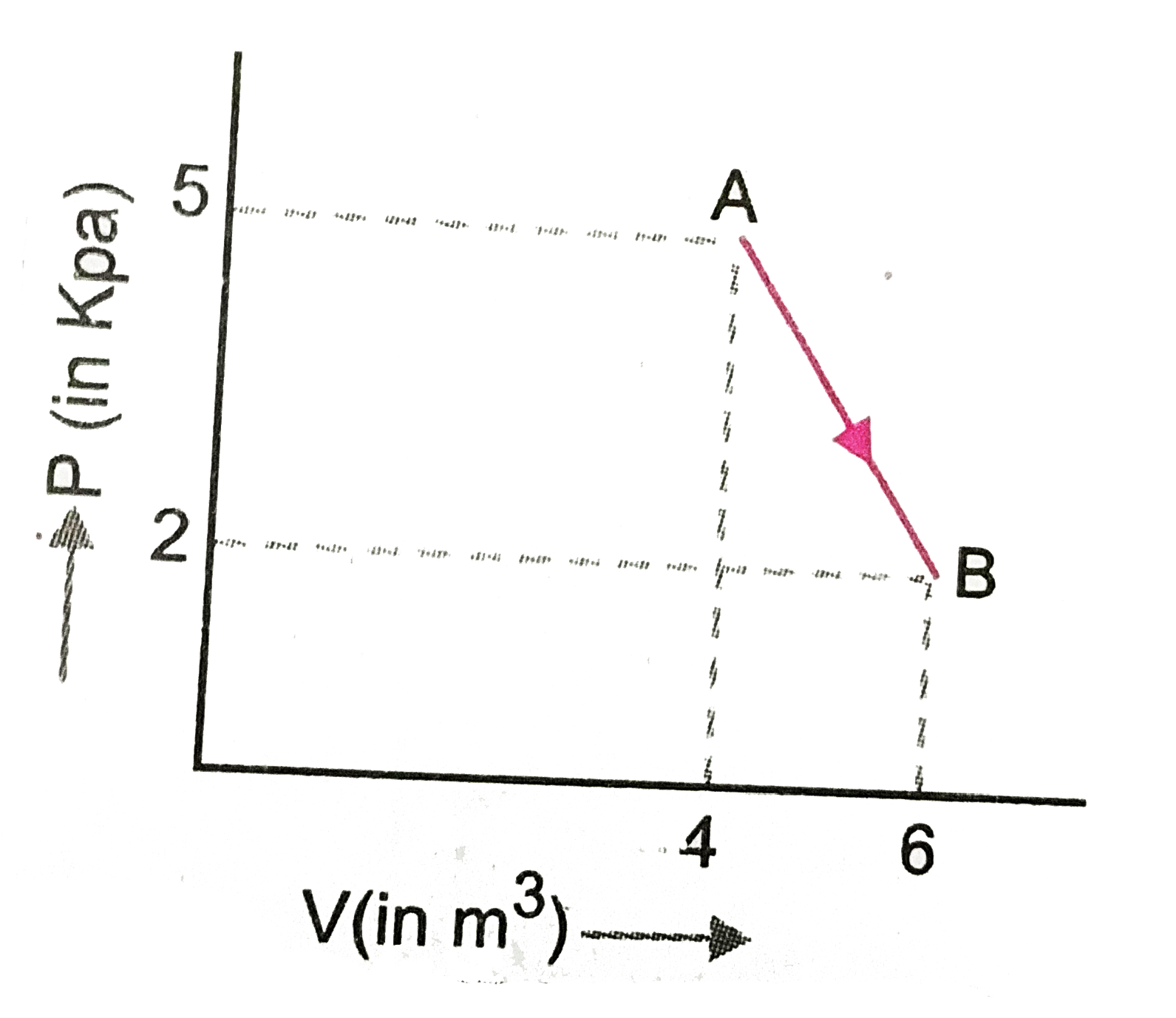
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is $(γ = 3 / 5)$

A

$- 20 k J$

B

$20 J$

C

$- 12 k J$

D

$20 k J$

Video Solution

Text Solution

Verified by Experts

$T_{A} = \frac{P_{A} V_{A}}{n R}, T_{B} = \frac{P_{B} V_{B}}{n R}$
${(Δ U)}_{A \to B} = n C_{V} Δ T = n . \frac{5 R}{2} (T_{B} - T_{A})$
$= \frac{5 n R}{2} (\frac{P_{B} V_{B} - P_{A} V_{A}}{n R})$
$= \frac{5}{2} (P_{B} V_{B} - P_{A} V_{A})$
$= \frac{5}{2} (2 \times 6 - 5 \times 4) \times 10^{3} = - 20 k J$

Updated on:21/07/2023

|

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure. The change in internal energy of the gas during the transition is

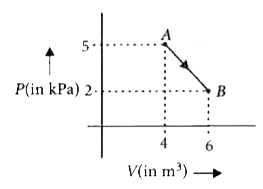A20 J
B $- 12 k J$
C20 kJ
D $- 20 k J$
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure,

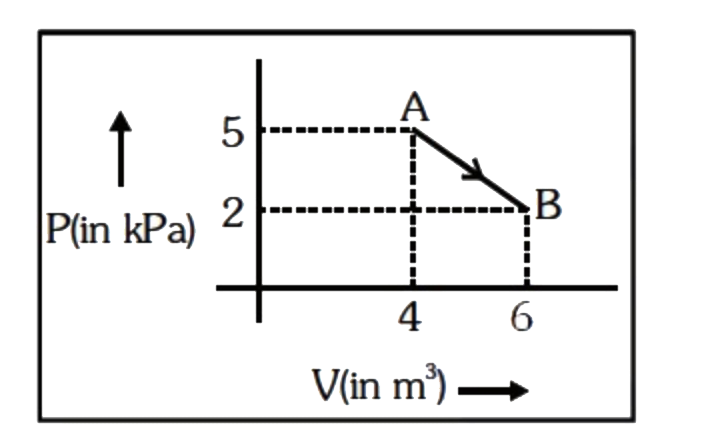
The change in internal energy of the gas during the transition is :
A20 kJ
B $- 20 k J$
C20 J
D $- 20 k J$
One mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in (figure). The change in internal energy of the gas during the transition is $(γ = 3 / 5)$

A $- 20 K J$
B20 J
C $- 12 K J$
D20 KJ

CP SINGH-NEET PREVIOUS YEAR-Solved Questions

Home
Ask Doubt
Profile