Consider the situation shown in figure. The frame is made of the same material and has a uniform cross-section area everywhere. Calculate the amount of heat flowing per second through a cross section of the bent part if the total heat taken out per second from the end at 100∘C is 130J .
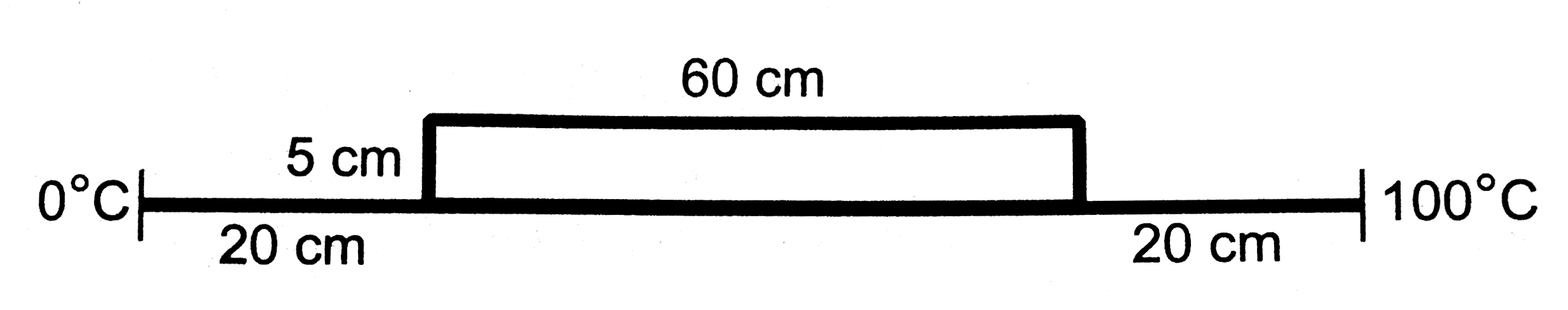
130J
60J
70J
80J
The correct Answer is:B
(2) Length AD=60cm
Length of bent part =5+60+5=70cm
Resistance ∝ length
R1=70R,R2=60R
i1=R2R1+R2i=60R70R+60R×130
=60J

Topper's Solved these Questions
Similar Questions
Conside the situation shown in figure. The frame is made of the same material and has a unifrom cross-section area everywhere. Calculate the amount of heat flowing per second through a cross section of the bent part if the total heat taken out per second from the end at 100∘C is 130J .
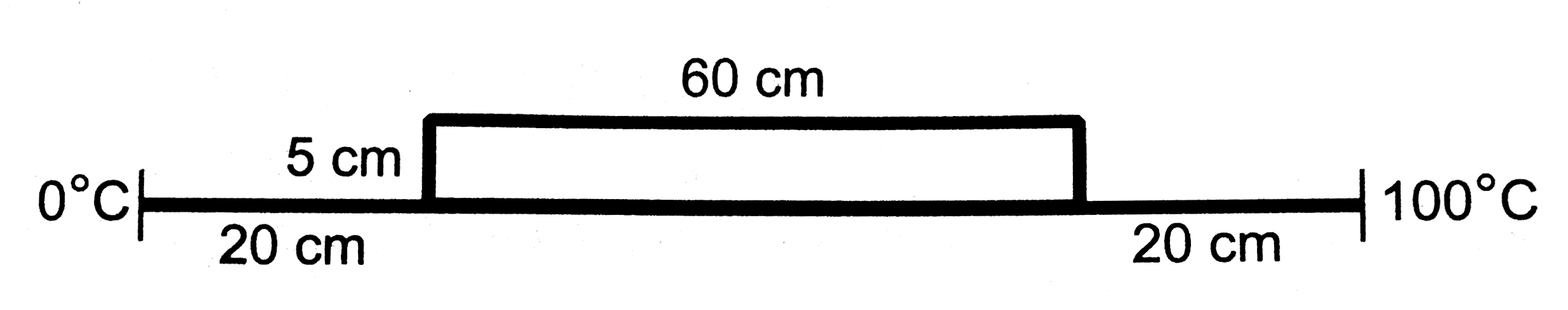
View SolutionConsider the situation shown in figure. The frame is made of the same material and has a uniform cross-sectional area everwhere. If amount of heat flowing per second through a cross-section of part A is 60J. The amount of total heat taken out per second from the end at 50∘C is 0.132×10nJ/s. Find 'n'.
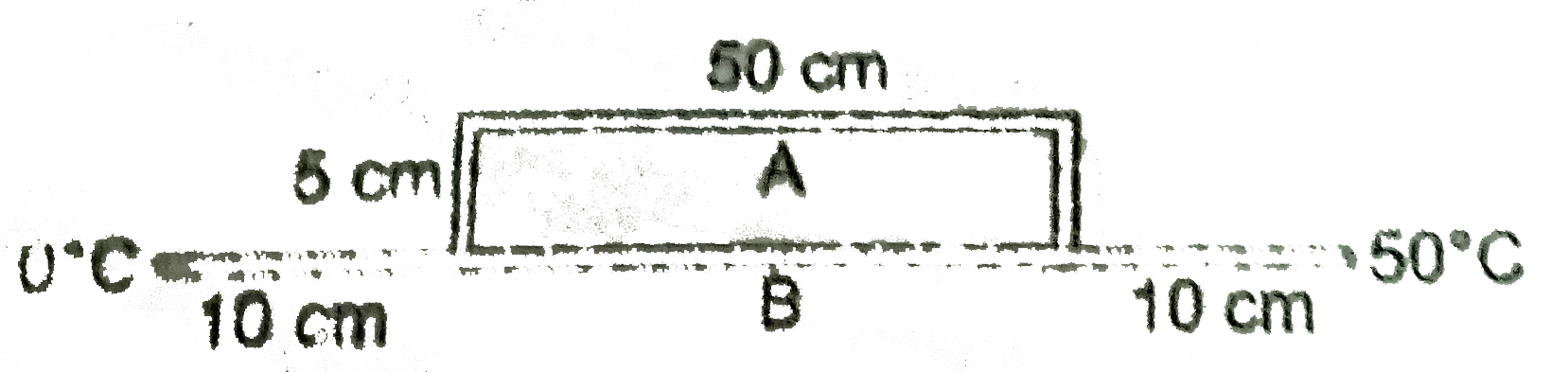
View Solution
Knowledge Check
A rod is made of uniform material and has non-uniform cross section. It is fixed at both the ends as shown and heated at mid-section. Which of the following are not correct?
 AForce of compression in the rod will be maximum at mid sectionBcomressive stress in the rod will be maximum at left endCsince rod in fixed at both the ends, its length will remain unchanged. Hence, no strain will be induced in it.Dnone of these
AForce of compression in the rod will be maximum at mid sectionBcomressive stress in the rod will be maximum at left endCsince rod in fixed at both the ends, its length will remain unchanged. Hence, no strain will be induced in it.Dnone of theseThe ratio of cross-sectional areas of two conducting wires made up of same material and having same length is 1: 2. What will be the ratio of heat produced per second in the wires, when same current is flowing in them?
A1:4B2:1C1:√2D1:1Two rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.
 A2πB1πCπDπ2
A2πB1πCπDπ2
Find the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1 . Thermal conductivity of the material of the rod is K.

View Solution(a) Three rod of lengths 20cm each and area of cross-section 1cm2 are joined to form a triangle ABC. The conductivities of the rods are KAB=50J/m−s−.∘C,KBC=200J/m−s−.∘C and KAC=400J/m−s−.∘C. The junctions A,B and C are maintained at 40∘C, 80∘C and 80∘C respectively. Find the rate of heat flowing through the rods AB,AC and BC.
(b) A semicircular rod is joineted as its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross-section of the simicircular rod to the heat transferred through a cross-section of the straight rod in a given time.
View SolutionA semicircular rods is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod formss a diameter of the other rod. The junction are maintaine dat different temperature. Find the ratio of the heat transffered through a cross section of the straigh rod in a given time.
View SolutionA metallic wire has variable cross sectional area. Cross sectional area at cd is twice the area at ab. The wire is connected to a cell as shown. find the ratio of heat dissipated per unit volume at section cd to that at section ab.
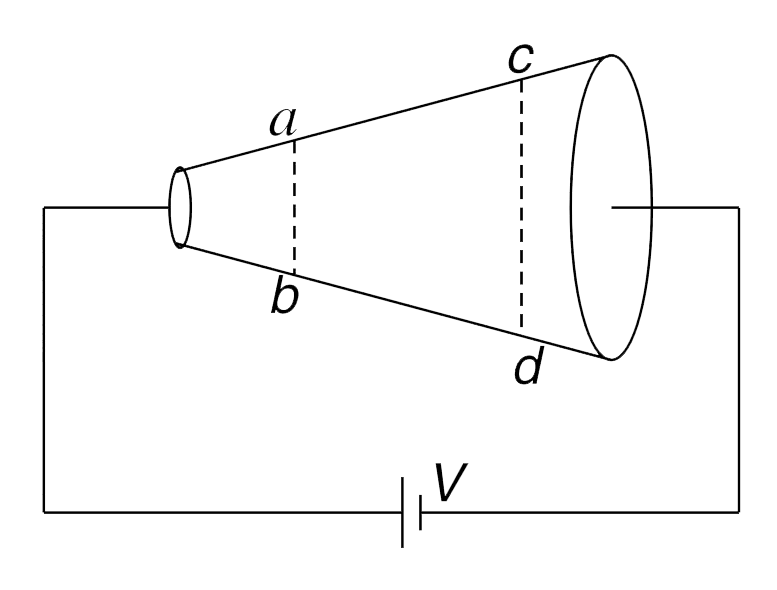
View SolutionAn irregular rod of same uniform material as shown in is conducting heat at a steady rate. The temperature gradient at varoius sections versus area of cross section graph will be
 .
.
View Solution

