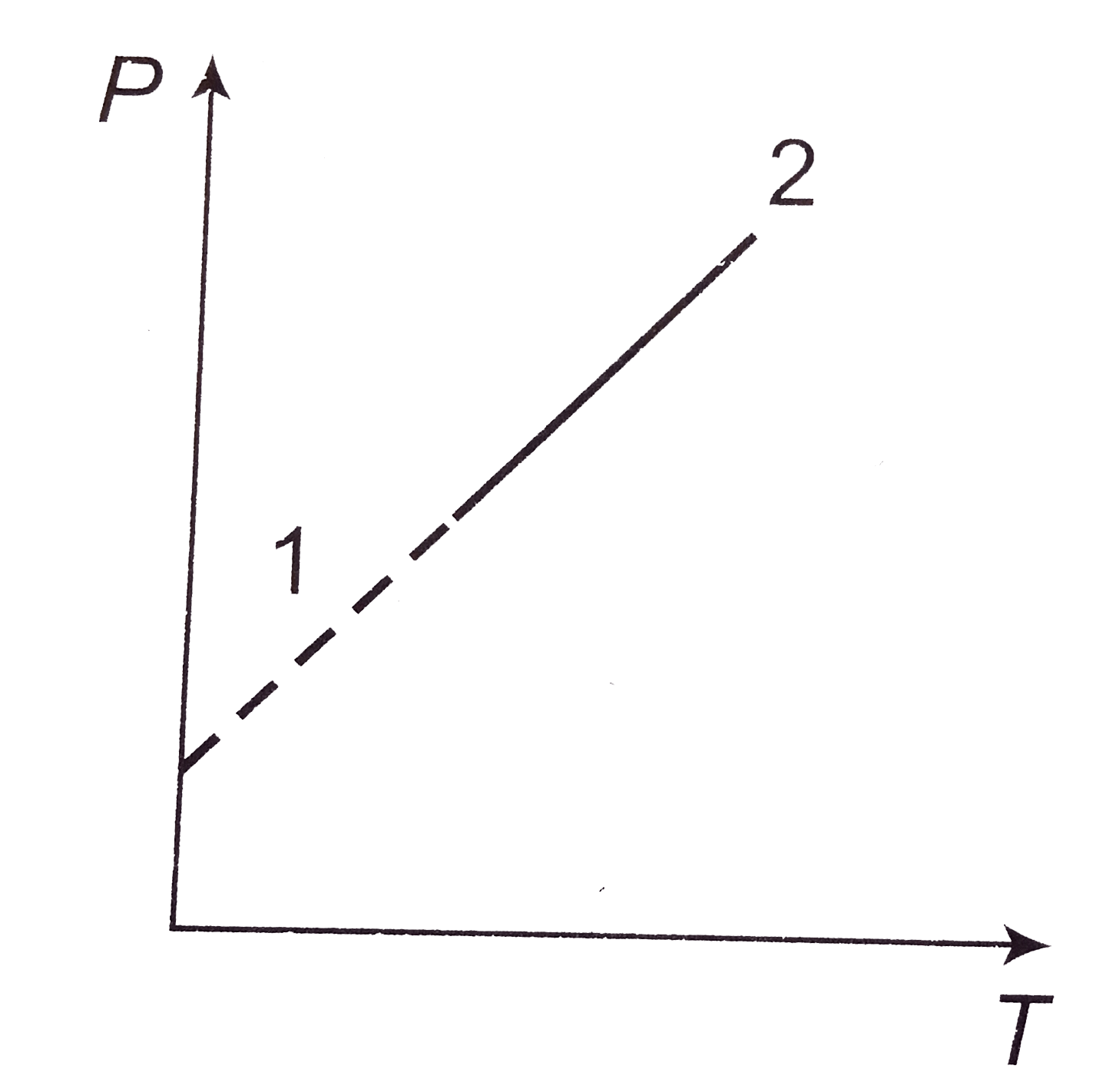
A pressure P, absolute temperature T, graph was obtained whe a given mass of a gas heated. During the heating process from the state 1 to the state 2, the volume
remained same
decreased
increased
none
The correct Answer is:C
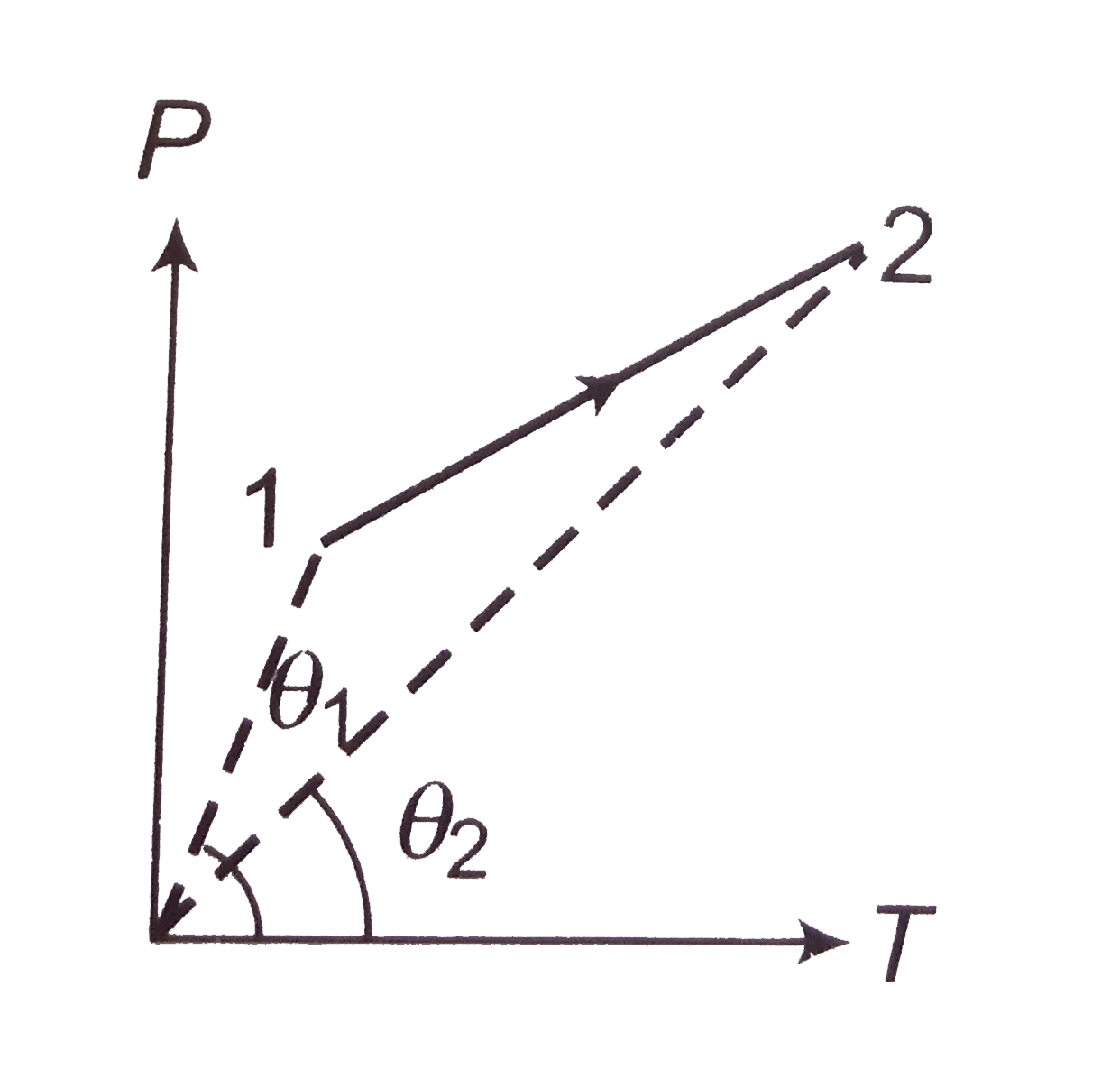
Slope : tanθ1=(PT)1=nRV1
tanθ2=(PT)2=nRV2
tanθ1>tanθ2
nRV1>nRV2
V2>V1
1→2 volume is increasing
Topper's Solved these Questions
Similar Questions
Knowledge Check
A volume V absolute temperature T diagram was obtained when a given mass of gas was heated. During the heating process from state 1 to 2, the pressure
_E01_062_Q01.png)
ARemain constantBDecreasedCChanged erraticallyDIncreasedAt pressure P and absolute temperature T a mass M of an ideal gas fills a closed container of volume V. An additional mass 2M of the same gas is added into the container and the volume is then reduced to V3 and the temperature to T3. The pressure of the gas will now be:
AP3BPC3PD9PThe P−T graph for the given mass of an ideal gas is shown in figure. Then the volume
_E01_022_Q01.png)
AincreasesBdecreasesCremains constantDdata insuficient
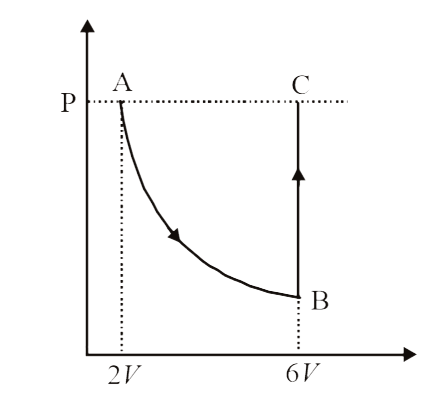
In the figure n mole of a monoatomic ideal gas undergo the process ABC as shown in the P-V diagram. The process AB is isothermal and BC is isochoric. The temperature of the gas at A is T0 total heat given to the gas during the process ABC is measured to be
Q. Heat absorbed by the gas in the process BC
View Solution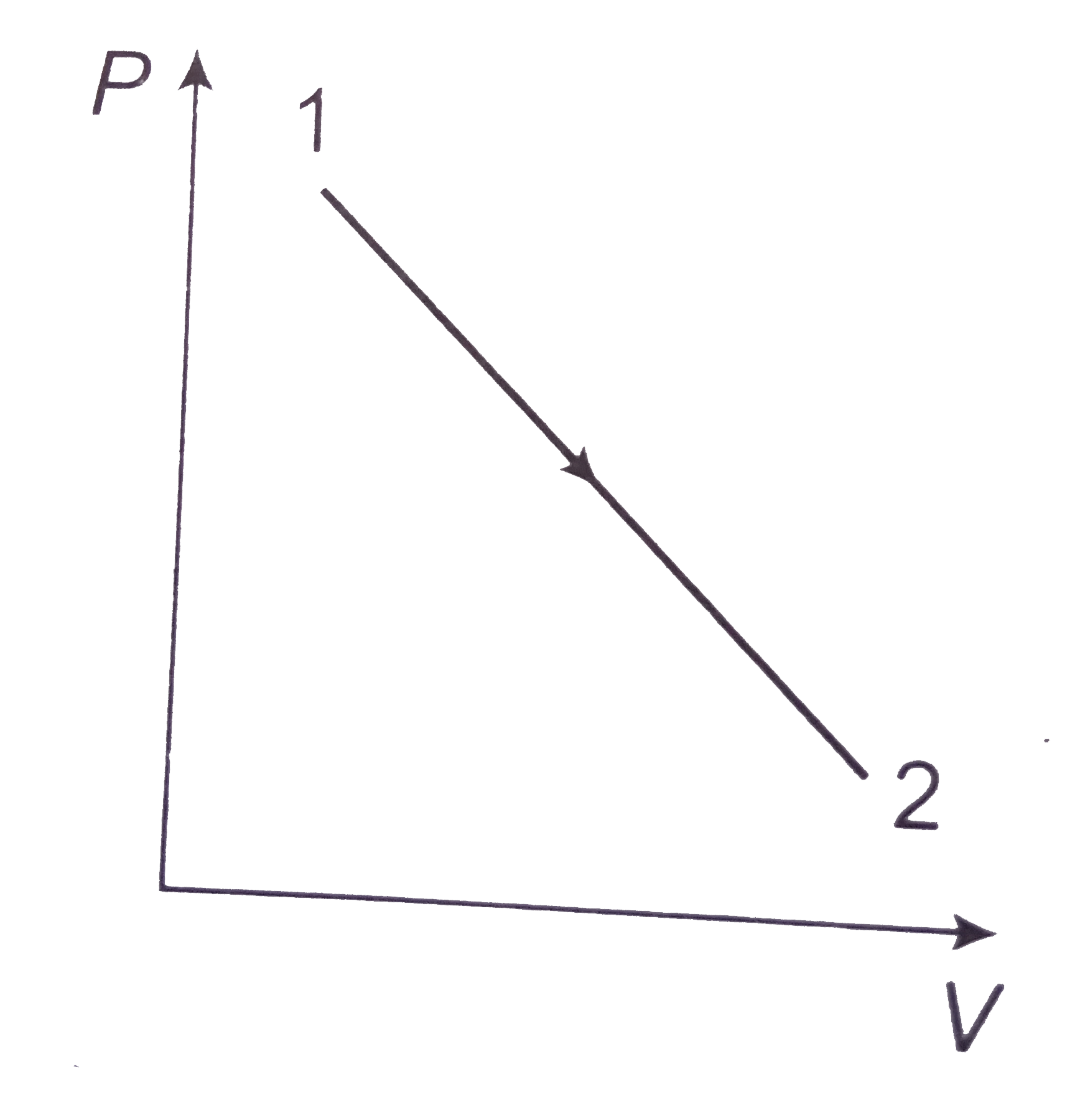
P−V graph was obtained from state 1 to state 2 when a given mass of a gas is subjected to temperature changes during the process the gas is
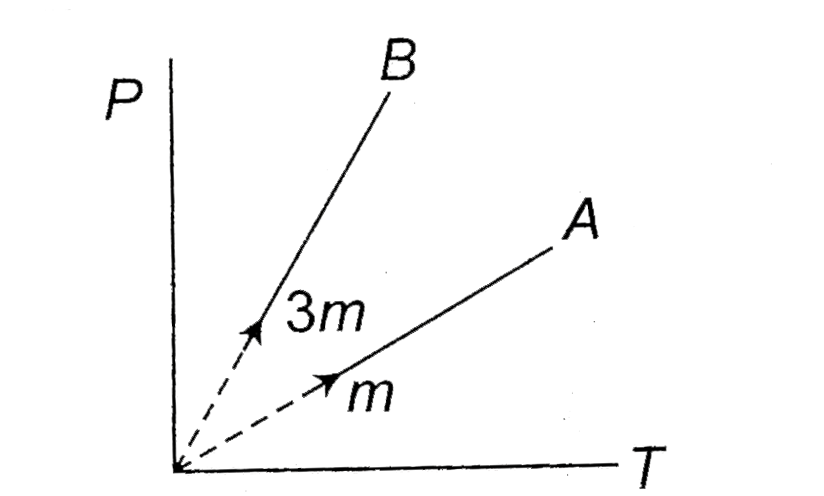
View SolutionTwo different masses m and 3m of an ideal gas are heated separately in a vessel of constant volume, the pressure P and absolute temperature T, graphs for these two cases are shown in the figure as A and B. The ratio of slopes of curves B to A is
View SolutionFor an adiabatic change in a gas, if P,V,T denotes pressure, volume and absolute temperature of a gas at any time and γ is the ratio of specific heats of the gas, then which of the following equation is true?
View SolutionA ideal gas has pressure 'p', volume 'V' and absolute temperature 'T'. It 'm' is the mass of each molecules and 'K' is the Boltzmann constant , the density of the gas is
View Solution