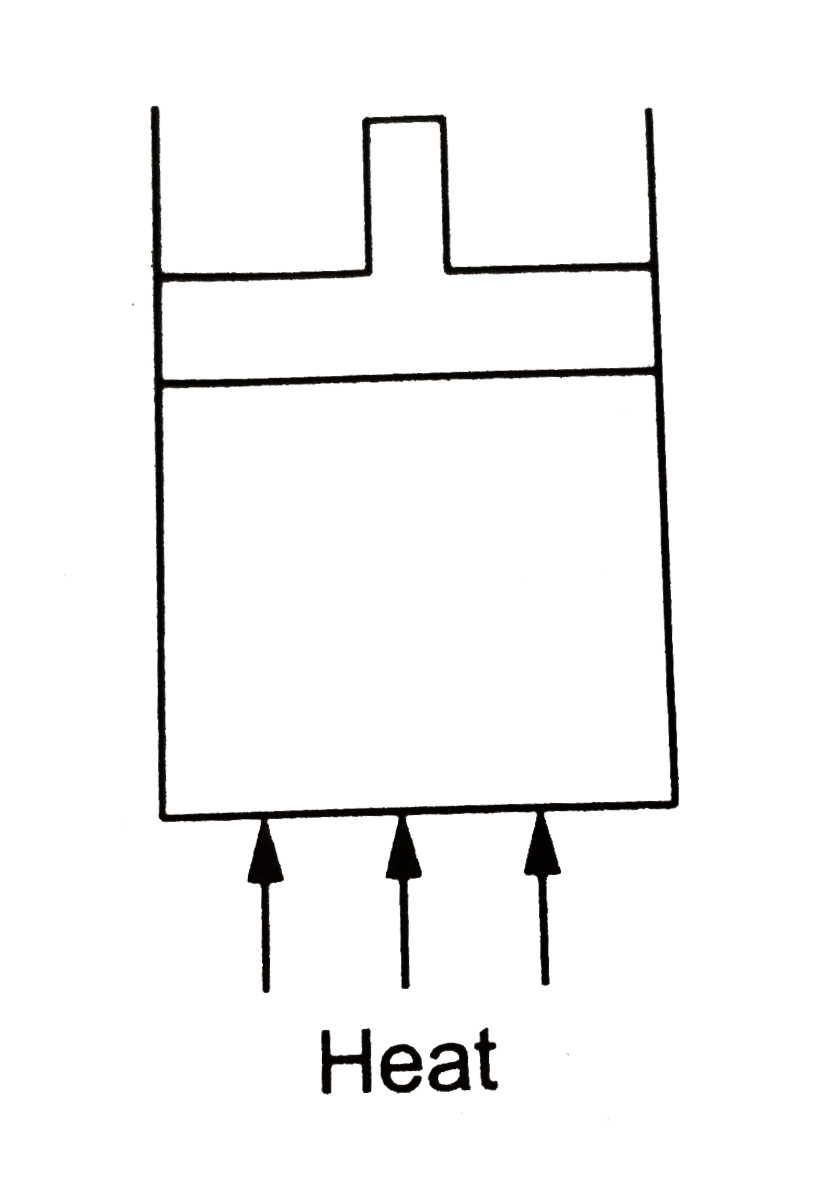
Figure shows two vessels with adiabatic walls, one containing 0.1 g of

Two identical vessels contain helium and hydrogen gases at same temperature, then
Aaverage kinetic energy per mole of hydrogen = average kinetic energy per mole of helium
Baverage translational kinetic energy per mole of hydrogen = average translational kinetic energy per mole of helium
Caverage kinetic energy per mole of hydrogen $= \frac{3}{5}$ average kinetic energy per mole of helium
Daverage kinetic energy per mole of hydrogen $= \frac{5}{3}$ average kinetic energy per mole of helium
Freundlich equation for adsorption of gases (in amount of Xg) on a solid (in amount od mg) at constant temperature can be expressed as
A $\frac{log (x)}{m} = log p + \frac{1}{n} log K$
B $\frac{log (x)}{m} = log K + \frac{1}{n} log p$
C $\frac{x}{m} \propto p^{n}$
D $\frac{x}{m} = log p + \frac{1}{n} log K$
Freundlich equation for adsorption of gases ( in amount of x g) of a solid ( in amount of m g ) at constant temperature can be expressed as
A $log (\frac{x}{m}) = log p + \frac{1}{n} log k$
B $log (\frac{x}{m}) = log k + \frac{1}{n} log p$
C $\frac{x}{m} \propto p^{n}$
D $\frac{x}{m} = log p + \frac{1}{n} log k$

Two identical vessels contain helium and hydrogen gases at same temperature, then