A U-tube containing a liquid is accelerated horizontally with a constant acceleration $a_{0}$ . If the separation between the vertical limbs is l find the difference in the heights of the liquid in the two arms.

A

$a d / g$

B

$2 d a / g$

C

$d a / 2 g$

D

$d tan (a / g)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let $A$ : area of cross-section of tube
$ρ$ : density of the liquid
Mass of the liquid in $A B = m = ρ A d$
$P_{A} = ρ g h_{2}, P_{B} = ρ g h_{1}$
Net force = mass $\times$ acceleration
$(P_{A} - P_{B}) A = m a = ρ A d a$
$ρ g (h_{2} - h_{1}) A = ρ A d a$
$(h_{2} - h_{1}) g = d a$
$h_{2} - h_{1} = \frac{d a}{g}$ .
.

|

Updated on:21/07/2023

Class 11 PHYSICS MECHANICAL PROPERTIES OF FLUIDS

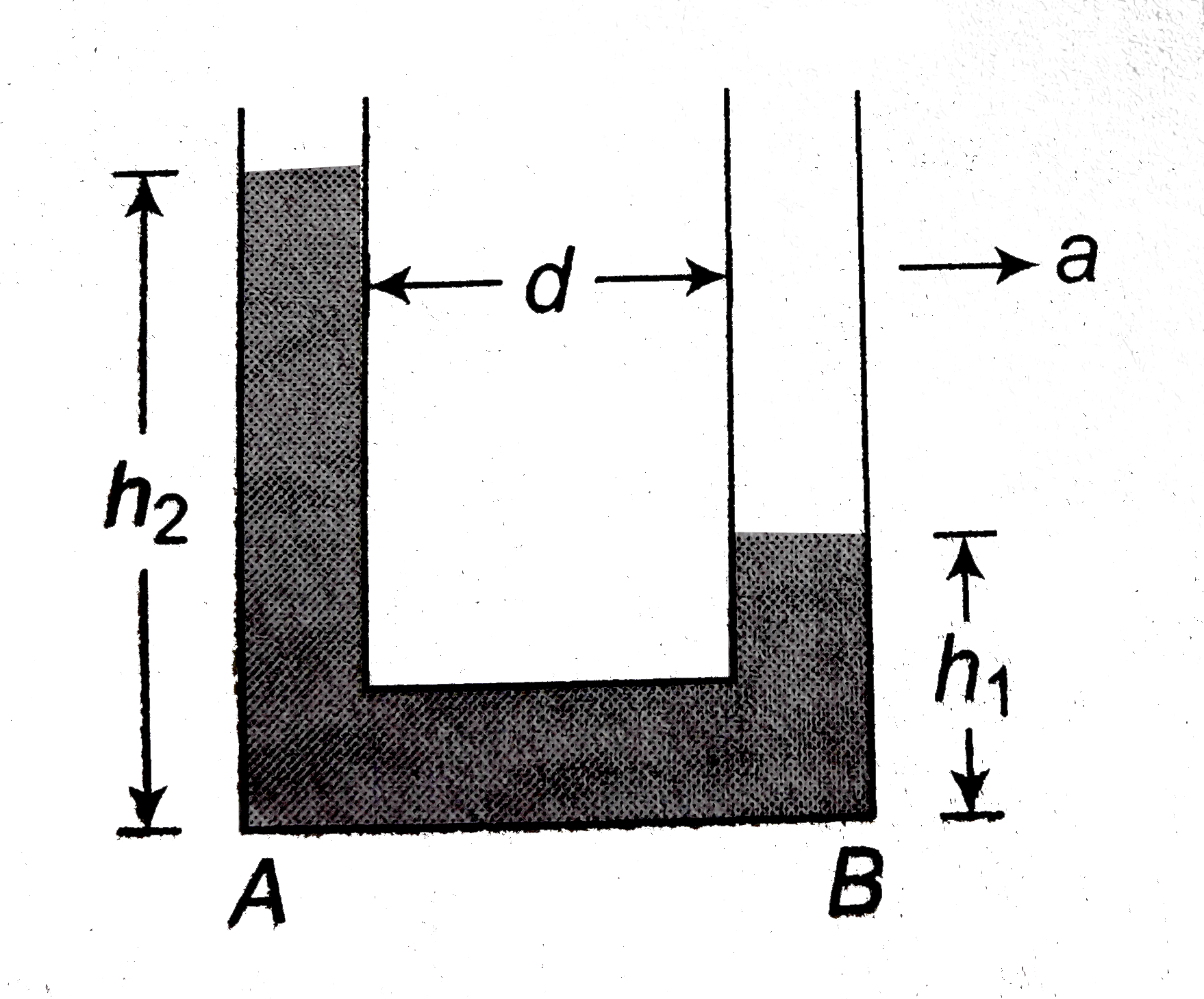Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Fig, shows a U-tube of uniform cross-sectional area $A$ accelerated with acceleration $a$ as shown. If $d$ is the seperation between the limbs. Then the difference in the levels of the liquid in the $U - t u b e$ is

A $\frac{a d}{g}$
B $\frac{g}{a d}$
C $a d g$
D $a d + g$
Question 2 - Select One
A U-tube containing a liquid moves with a horizontal acceleration a along a direction joining the two vertical limbs. The separation between these limbs is d. The difference in their liquid levels is
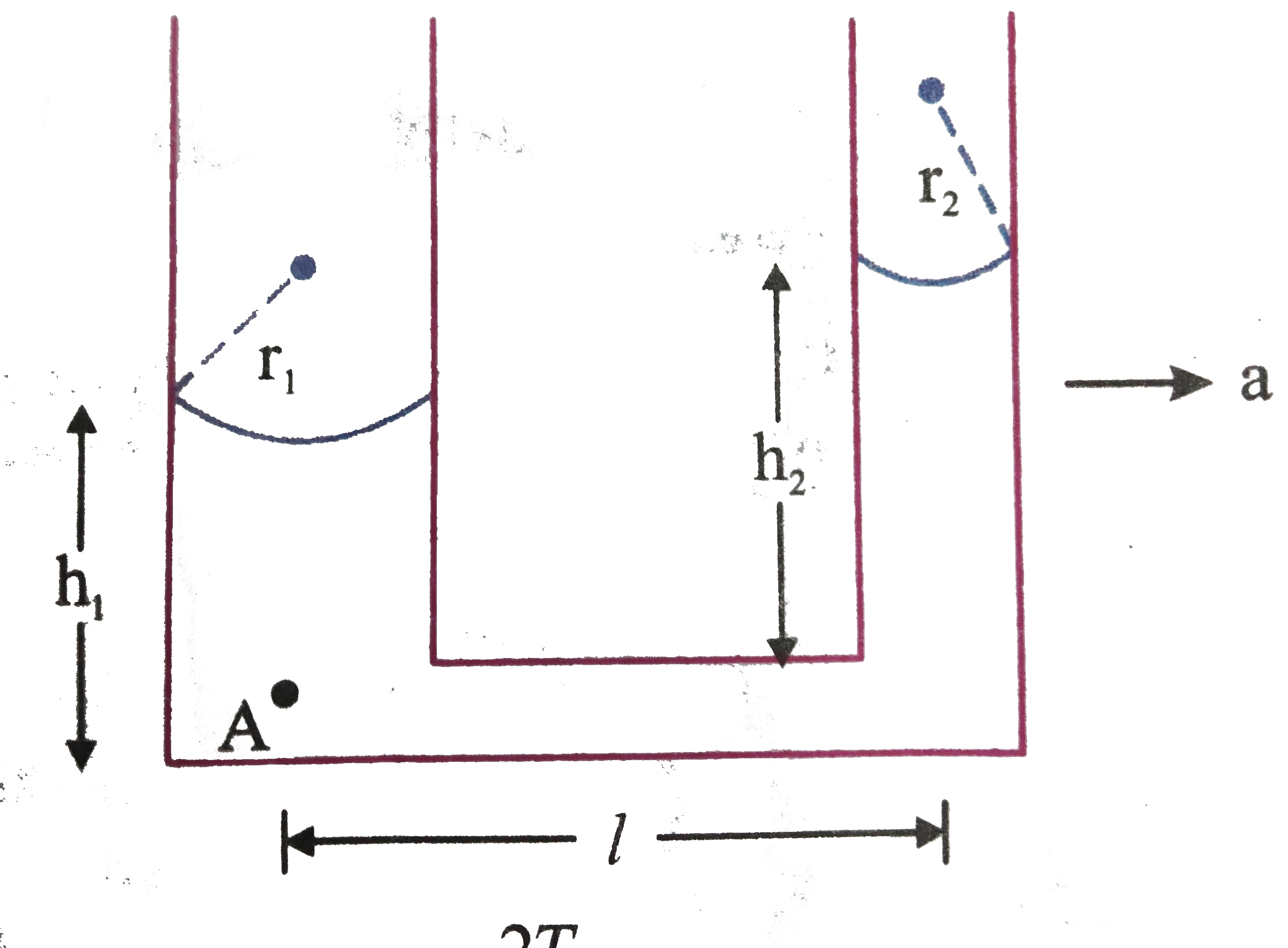
A $a d / g$
B $2 d a / g$
C $d a / 2 g$
D $d tan (a / g)$
Question 3 - Select One
A vertical U-tube contains a liquid of density $ρ$ and surface tension T. if the radius of the meniscus of liquid in the limbs of the U-tube are $R_{1}$ and $R_{2}$ find the difference in the liquid column in the limbs.
A $Δ h = \frac{T (R_{1} - R_{2})}{ρ g R_{1} R_{2}}$
B $Δ h = \frac{2 T (R_{1} - R_{2})}{ρ g R_{1} R_{2}}$
C $Δ h = \frac{2 T (R_{1} + R_{2})}{ρ g R_{1} R_{2}}$
D $Δ h = \frac{4 T (R_{1} - R_{2})}{ρ g R_{1} R_{2}}$

CP SINGH-FLUID MECHANICS-Exercises

Home
Ask Doubt
Profile