Calculate the capacitance of a parallel plate capacitor, with plate area A and distance between the plates d, when filled with a dielectric whose permittivity varies as
∈(x)=∈0+kx(0<x<d2),∈(x)=∈0+k(d−x)(d2<x≤d).

The given capacitor is equivalent to two capacitors in series. Let C1 and C2 be their capacities. Then
1C=∫[1dC1+1dC2]
Consider an element of width dx at a distance x from the left plate. Then
dC1=(ε0+kx)Adxfor0<x<d2
and dC2={∈0+k(d−x)}Adxford2<x≤d
on substituting these two values we get
1C−∫1dC=2KAln(2∈0+Kd2∈0)⇒C=KA2ln(2∈0+Kd2∈0).
Topper's Solved these Questions
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:C.U.Q
Explore 54 Videos
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:Assertion & Reasoning
Explore 16 Videos
- ATOMS Book:NARAYNAChapter:ATOMS Exercise:EXERCISE -4
Explore 47 Videos
- COMMUNICATION SYSTEMBook:NARAYNAChapter:COMMUNICATION SYSTEMExercise:Level-II(H.W)
Explore 25 Videos
Similar Questions
Calculate the capacitance of a parallel plate condenser, with plate area A and distance between plates d, when filled with a dielectric whose dielectric constant varies as,
K(x)=1+βx∈0 0<x<d2, K(x)=1+β∈0(d−x) d2<x<d.
For what value of β would the capacity of the condenser be twice that when it is without any dielectric?
View SolutionThe plates of a parallel plate capacitance 1.0 F are separated by a distance d =1 cm. Find the plate area .
View Solution
Knowledge Check
The capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
 Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2d
Aε0A1dBε0A2dCε0(A1+A2)2dDε0√A1A2dThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
ACV22dBC2V22d2CC2V2d2DV2dC
A parallel plate capacitor with plate area 'A' and distance of separation 'd' is filled with a dielectric. What is the capacity of the capacitor when permittivity of the dielectric varies as : ε(x)=ε0+kx, for (0<x≤d2)
ε(x)=e0+k(d−x), for (d2≤x≤d)
View SolutionThe distance between the plates fo a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates, what will be the new capacity ?
View SolutionIn a parallel plate capacitor distance between the plate is 'd'. If dielectric of variable permeability is filled as
ε(x)=ε0+kx,0<x≤d2
ε(x)=ε0+k(d−x),d2<x≤d
Find capacitance.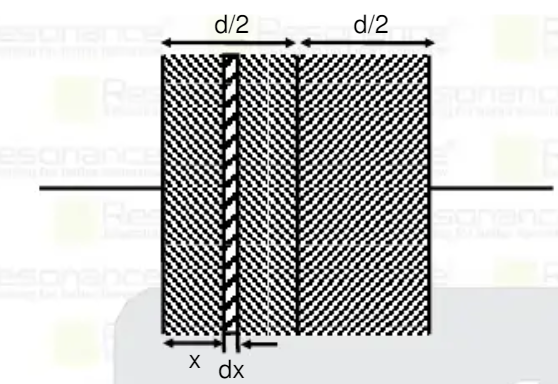
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.
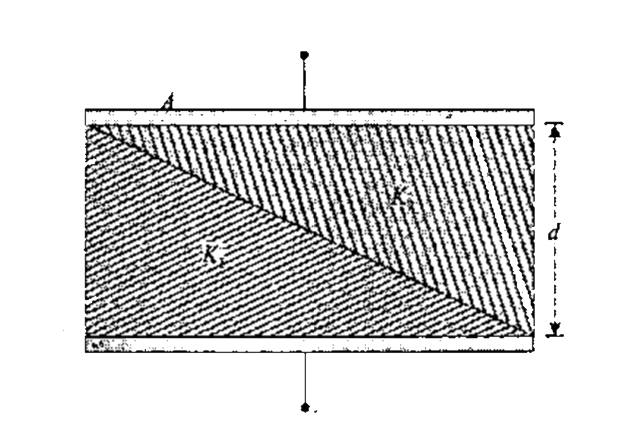
View SolutionThe capacitance of a parallel plate capacitor with plate area A and separation d is C. The space between the plates in filled with two wedges of dielectric constants K1 and K2 respectively. Find the capacitance of resulting capacitor.

View SolutionThe' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View Solution

