In a capillary rise, find the heat developed taking all standard notations as described in the foregoing section.
Q=2πTcos2θρg
Q=2πr2Tcos2θρg
Q=2πT2sin2θρg
Q=2πT2cos2θρg
The correct Answer is:D
As the liquid rises, positive work is done by surface tension in pulling the liquid up by a distance h which is given as
WST=Fyh where Fy=(Tcosθ)2πr
Wgr=−ΔU=mgyCM,
where YCM=h2 and m=(πr2h)ρ
Then, ΔU=πr2ρgh22 where h=2Tcosθρgr This gives applying first law of thermodynamics, the heat dissipated Q can be gives as WST=Q+ΔU
From the above equations,
we have Q=2πT2cos2θρg
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:integer Type Questions
Explore 25 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Level 1 (H.W)
Explore 55 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Paragraph Type Questions
Explore 5 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBook:NARAYNAChapter:MATHEMATICAL REVIEW & PHYSICAL WORLDExercise:C.U.Q
Explore 13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
Similar Questions
Knowledge Check
A narrow capillary tube when dipped in beaker containing water, the rise is 20 cm . If the area of cross section of the bore is reduced to (1/4)th calue , water will rise to a height of
A10 cmB20 cmC40 cmD80 cmIf L is the capillary rise or dip and A the cross sectional area of the tube, other condition being the same, then
ALA= constantBL√A= constantCLA= constantDL√A= constantWater rises to a height h in a capillary tube when dipped vartically . If another capillary tube of the same material with half the bore cross section is dipped vertically rise of water in this case
A2hBh/2C√2hDh√2
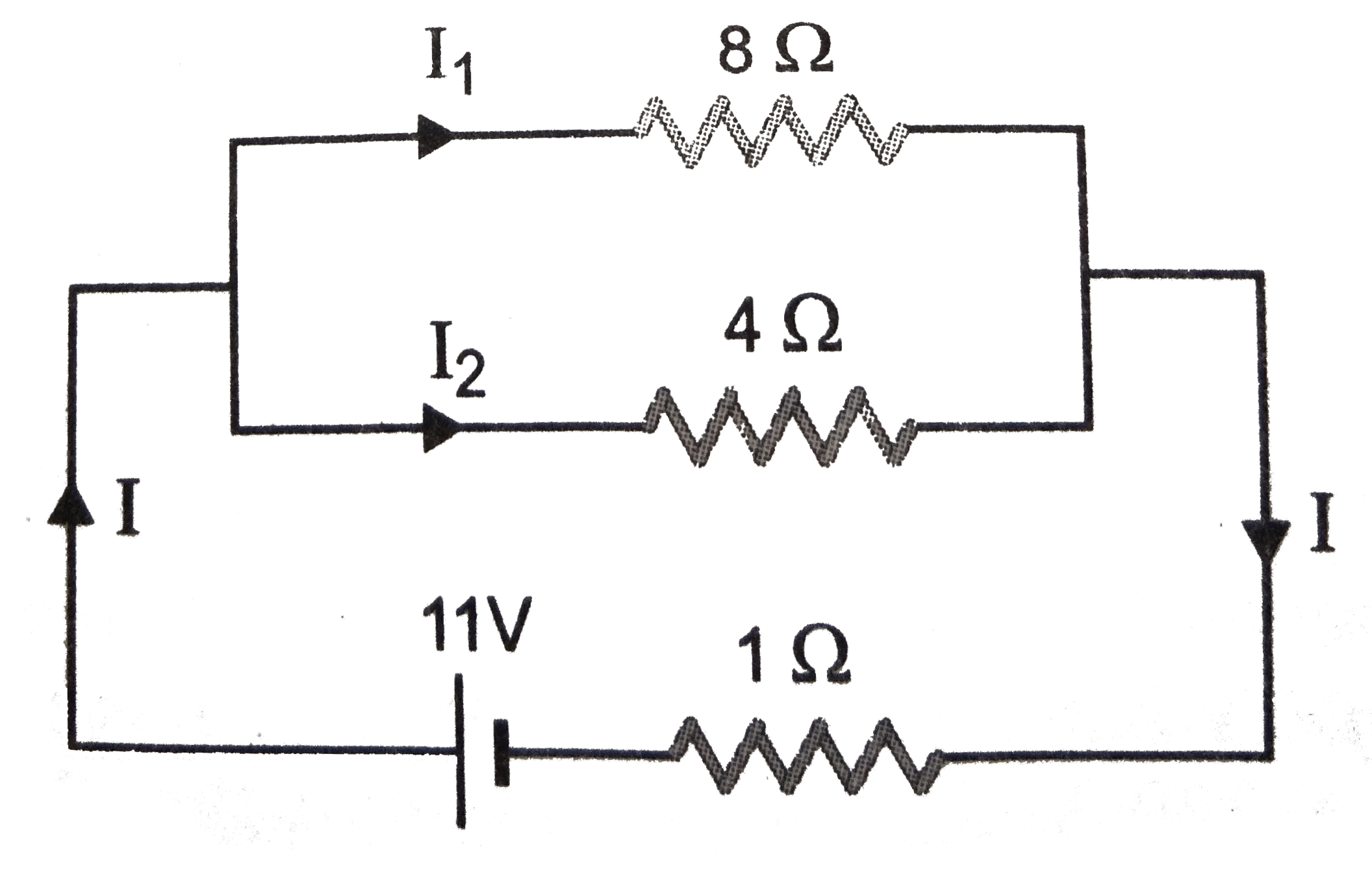
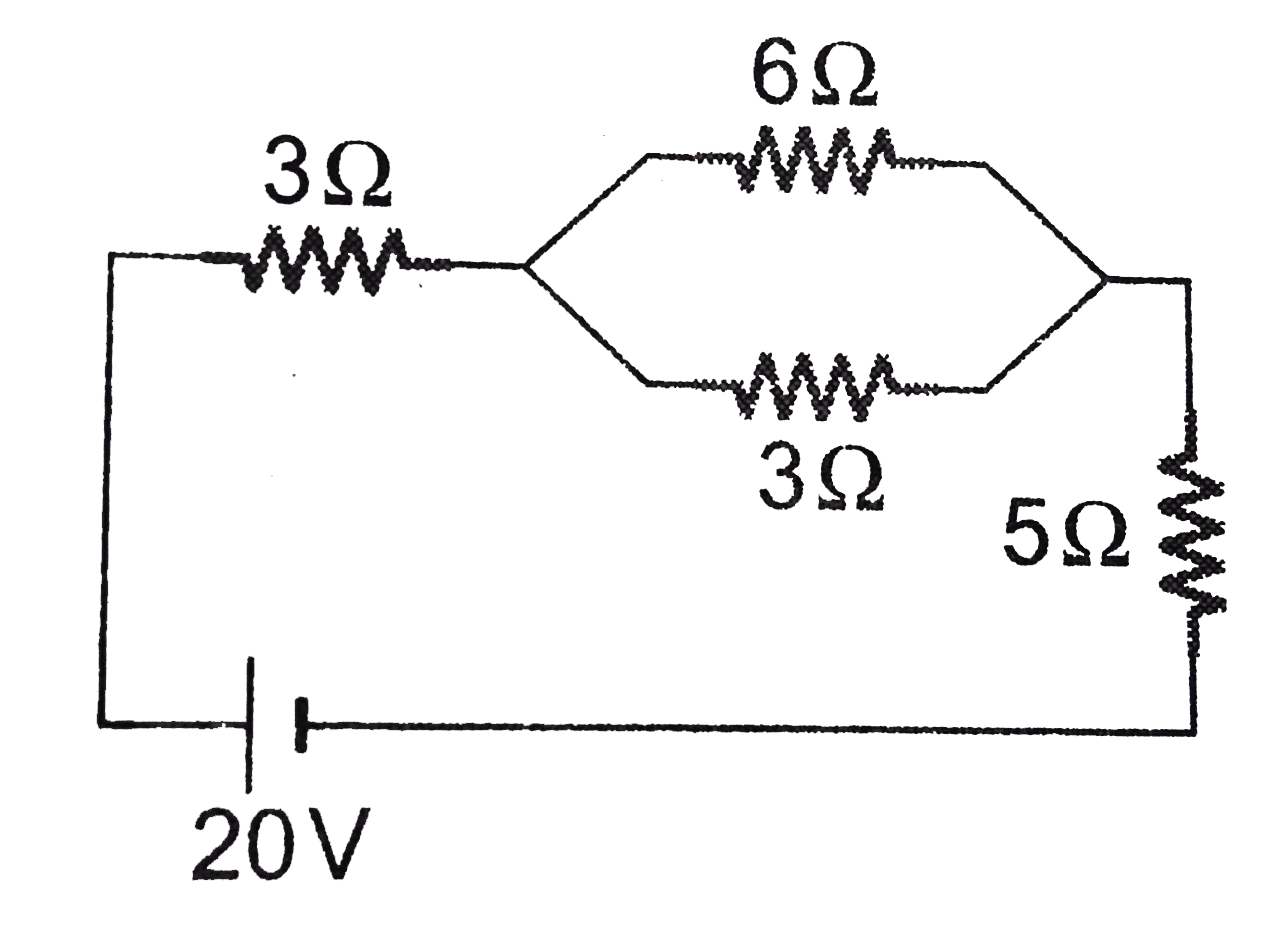
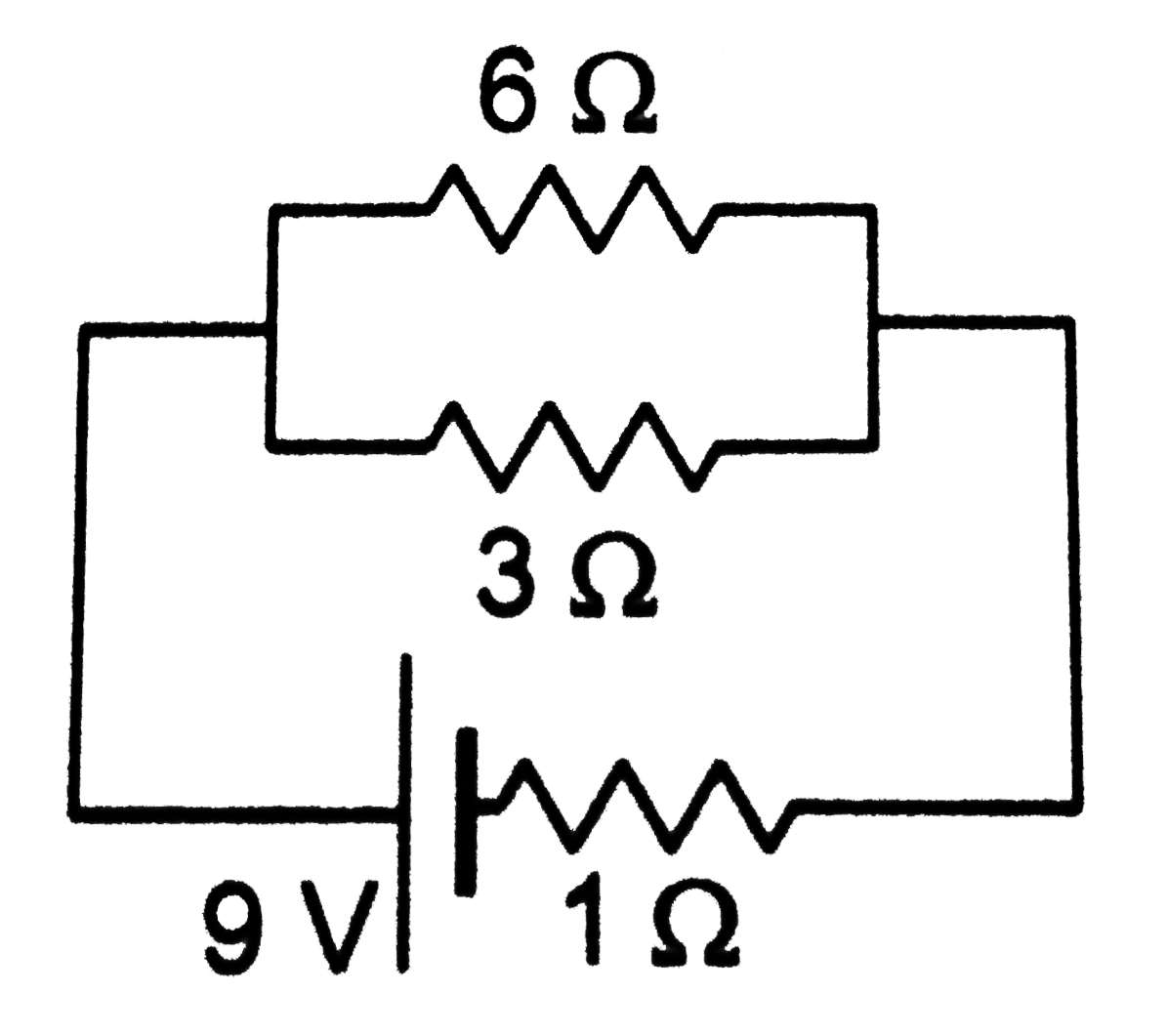
Find the heat developed in eachof the three resistors shown in figure in 1 minute.
View SolutionThe current in the inner coil is I=2t2. Find the heat developed in the outer coil between t =0 and t seconds. The resistance of the outer coil is R and take b>>a.

View SolutionWater rises to a height 3.2 cm in a glass capillary tube. Find the height to which the same water will rise in another glass capillary having half area of cross-section.
View SolutionWhen a capillary tube of radius r is immersed in a liquid of density ρ, the liquid rises to a height h in it. If m is the mass of the liquid in the capillary tube, find the potential energy of this mass of the liquid in the tube.
View SolutionThe lower end of a capillary tube of radius r cm is placed vertically in water. What is the heat evolved if water rise upto a height h in the capillary tube ?
View Solution