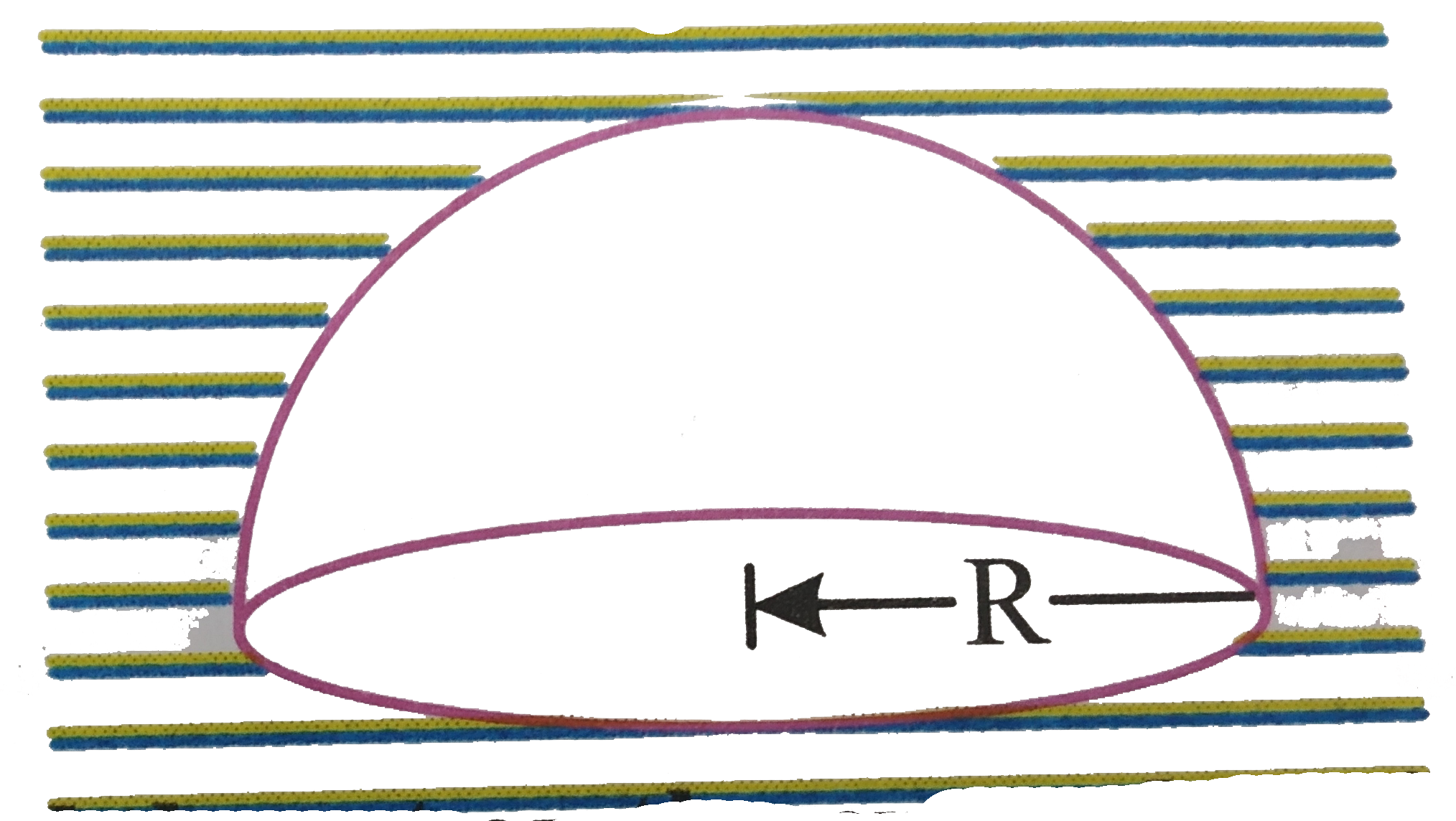
A solid hemisphere of radius R is made to just sink in a liquid of density ρ find the
πR3ρg3
πR3ρg2
0
πR3ρg
The correct Answer is:C
conceptual
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Paragraph Type Questions
Explore 5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Single Answer Questions
Explore 108 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:More Than One Alternative Type Question
Explore 32 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBook:NARAYNAChapter:MATHEMATICAL REVIEW & PHYSICAL WORLDExercise:C.U.Q
Explore 13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
Similar Questions
A solid hemisphere of radius R is made to just sink in a liquid of density ρ. Find a. the vertical thrust on the curved surface b. the vertical thrust on the flat surface c. the side thrust on the hemisphere. d. the total hydrostatic force acting on the hemisphere.
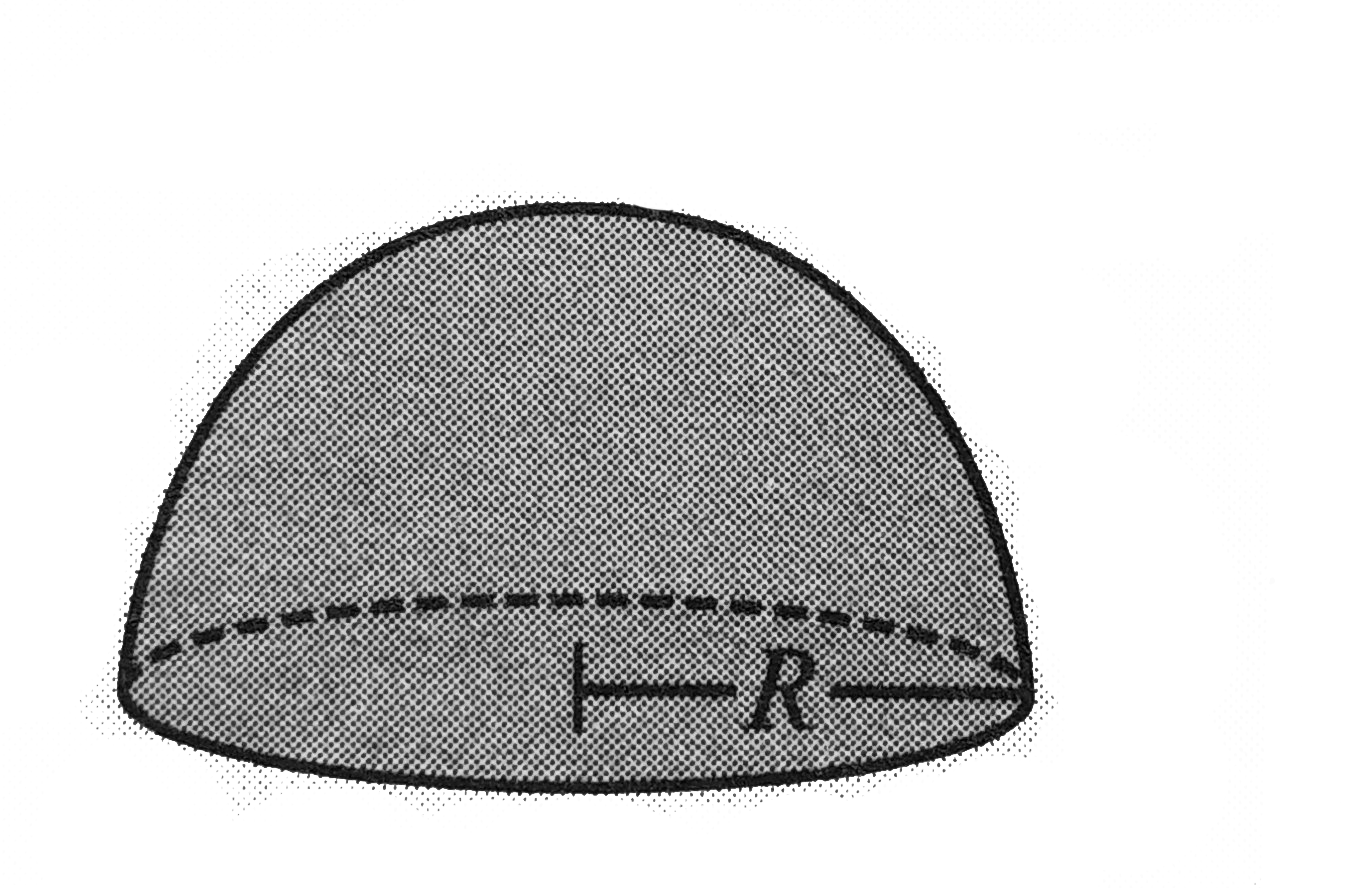
View SolutionA solid hemisphere of radius R is mounted on a solid cylinder of same radius and density as shown .the height of cylinder is such that the resulting centre of mass is at O. if radius of sphrere is 2√2m, what is the height of the cylinder (in m ) ?
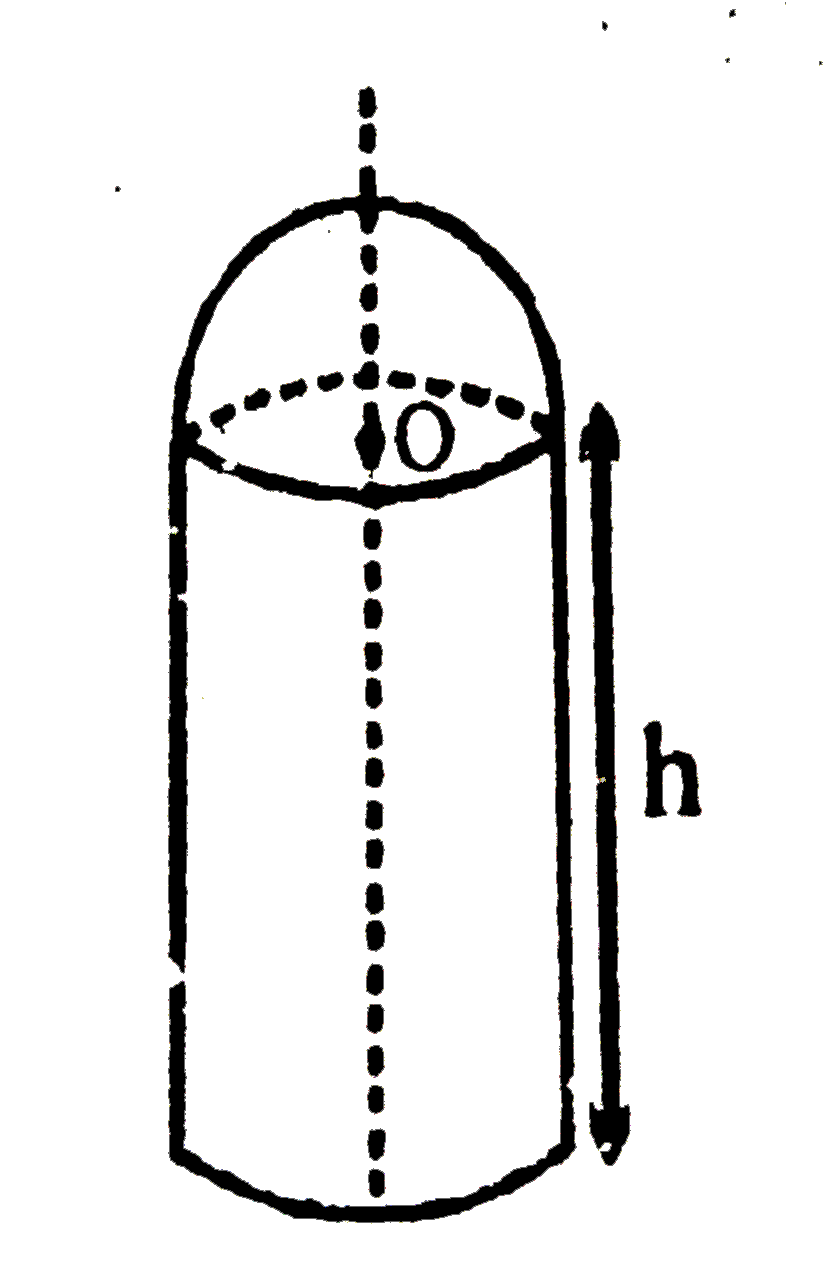
View Solution
Knowledge Check
A uniform solid sphere of radius R is in equilibrium inside a liquid whose density varies with depth from free surface as ρ=ρ0(1+hh0) where h is depth from free surface. Density of sphere σ will be :
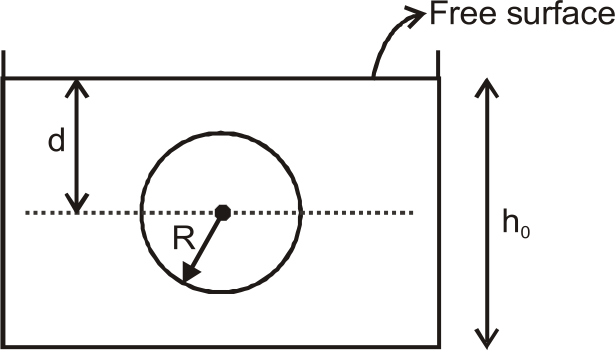 Aσ=ρ0(1+d2h0)Bσ=ρ0(1−d2h0)Cσ=ρ0(1+2dh0)Dσ=ρ0(1+dh0)
Aσ=ρ0(1+d2h0)Bσ=ρ0(1−d2h0)Cσ=ρ0(1+2dh0)Dσ=ρ0(1+dh0)A sphere of radius R and density ρ1 is dropped in a liquid of density σ. Its terminal velocity is v1. If another sphere of radius R and density ρ2 is dropped in the same liquid, its terminal velocity will be:
A(ρ2−σρ1−σ)v1B(ρ1−σρ1−σ)v1C(ρ1ρ2)v1D(ρ2ρ1)v1A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder bby the liquid is
 AMgBMg - h ρ gCMg+πR2hρgDρg(V+πR2h)
AMgBMg - h ρ gCMg+πR2hρgDρg(V+πR2h)
A solid sphere of radius R has a mass distributed in its volume of mass density ρ=ρ0 r, where ρ0 is constant and r is distance from centre. Then moment of inertia about its diameter is
View SolutionThere is a hemisphere of radius R having a uniform volume charge density ρ. Find the electric potential and field at the centre
View SolutionTwo solid spheres A and B each of radius R are made of materials of densities ρA and ρB respectively. Their moments of inertia about a diameter are IA and IB respectively. The value of IAIB is
View SolutionA rubber ball of bulk modulus B is taken to a depth h of a liquid of density ρ. Find the fractional change in the radius of the ball.
View SolutionWhen one end of a tube of radius r is immersed vertically in a liquid of density ρ, surface tension S, the rise of liquid in the tube is h and angle of contact is θ . If the tube is broken and its length is made h'(<h), then find the value of height of rise of liquid in the tube and angle of contact.
View Solution

