The mass of a metallic beam of uniform thickness and of length 6m is 60kg. The beam is horizontally and symmetrically lies on two vertical pillars which are separated by a distance 3m. A person of mass 75kg is walking on this beam. The closest distance to which the person can approach one end of the beam so that the beam does not tilt down is (neglect thickness of pillars)
30cm
20cm
15cm
10cm
The correct Answer is:A
To solve the problem step by step, we will analyze the situation using the principles of equilibrium and moments.
Step 1: Understand the System
We have a metallic beam of length 6 m and mass 60 kg, supported symmetrically on two pillars that are 3 m apart. A person with a mass of 75 kg is walking on this beam. We need to find the closest distance that the person can approach one end of the beam without causing it to tilt.
Step 2: Identify Key Points
- Let the beam be positioned horizontally with points A and D at the ends, and E and F as the pillars.
- The midpoint of the beam (C) is at 3 m from either end (A or D).
- The distance between the two pillars (E and F) is 3 m.
Step 3: Set Up the Free Body Diagram
- The weight of the beam acts downwards at its center (C), which is 60 kg × g.
- The weight of the person acts downwards at a distance x from point A.
- Let RE be the reaction force at pillar E and RF be the reaction force at pillar F.
Step 4: Conditions for Equilibrium
For the beam to be in equilibrium:
1. The sum of vertical forces must be zero:
RE+RF=60g+75g
2. The sum of moments about any point must be zero. We will take moments about point E.
Step 5: Calculate Moments about Pillar E
Taking moments about E (clockwise moments are positive):
- Moment due to the weight of the beam (60 kg) at a distance of 1.5 m from E (half of 3 m):
Moment due to beam=60g×1.5
- Moment due to the person (75 kg) at a distance of 3−x from E:
Moment due to person=75g×(3−x)
Setting the sum of moments about E to zero:
60g×1.5=75g×(3−x)
Step 6: Simplify the Equation
We can cancel g from both sides:
60×1.5=75×(3−x)
Calculating the left side:
90=75×(3−x)
Step 7: Solve for x
Expanding the right side:
90=225−75x
Rearranging gives:
75x=225−90
75x=135
x=13575=1.8 m
Step 8: Find the Closest Distance to the End
The closest distance to end A is x=1.8 m.
Step 9: Convert to Centimeters
To convert meters to centimeters:
1.8 m=180 cm
Final Answer
The closest distance to which the person can approach one end of the beam without causing it to tilt is 180 cm.
We have a metallic beam of length 6 m and mass 60 kg, supported symmetrically on two pillars that are 3 m apart. A person with a mass of 75 kg is walking on this beam. We need to find the closest distance that the person can approach one end of the beam without causing it to tilt.
- Let the beam be positioned horizontally with points A and D at the ends, and E and F as the pillars.
- The midpoint of the beam (C) is at 3 m from either end (A or D).
- The distance between the two pillars (E and F) is 3 m.
- The weight of the beam acts downwards at its center (C), which is 60 kg × g.
- The weight of the person acts downwards at a distance x from point A.
- Let RE be the reaction force at pillar E and RF be the reaction force at pillar F.
For the beam to be in equilibrium:
1. The sum of vertical forces must be zero:
RE+RF=60g+75g
2. The sum of moments about any point must be zero. We will take moments about point E.
Taking moments about E (clockwise moments are positive):
- Moment due to the weight of the beam (60 kg) at a distance of 1.5 m from E (half of 3 m):
Moment due to beam=60g×1.5
- Moment due to the person (75 kg) at a distance of 3−x from E:
Moment due to person=75g×(3−x)
60g×1.5=75g×(3−x)
We can cancel g from both sides:
60×1.5=75×(3−x)
Calculating the left side:
90=75×(3−x)
Expanding the right side:
90=225−75x
Rearranging gives:
75x=225−90
75x=135
x=13575=1.8 m
The closest distance to end A is x=1.8 m.
To convert meters to centimeters:
1.8 m=180 cm
The closest distance to which the person can approach one end of the beam without causing it to tilt is 180 cm.
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:NCERT based questions
Explore 15 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -I(H.W)
Explore 58 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-II(C.W.)
Explore 64 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A uniform beam of length 2 a rests in equilibrium with one end resting against a smooth vertical wall and with a point of its length resting upon a smooth horizontal rod which is parallel to the wall and at a distance b from it. The inclination of the beam to the vertical is sin−1(ba)13.
View SolutionA uniform board of mass M and length L rests on two spring scales. A person of mass m stands at a distance l from one end as shown in Fig. (a) The board and person are at rest. What is the reading of the two scales?
View Solution
Knowledge Check
A boy of mass 50kg is standing at one end of a boat of length 9m and mass 400kg. He runs to the other end. The distance through which the centre of mass of the boat boy system moves is
A0B1mC2mD3mIf two particles of masses 3kg and 6kg which are at rest are separated by a distance of 15m. The two particles are moving towards each other under a mutual force of attraction. Then the ratio of distances travelled by the particles before collision is
A2:1B1:2C1:3D3:1A man of mass m stands at the left end of a uniform plank of length L and mass M, which lies on a frictionaless surface of ice. If the man walks to the other end of the plank, then by what distance does the plank slide on the ice?
ALBMLm+MCmLMDmLm+M
A boat of 90kg is floating in still water. A boy of mass 30 kg walks from the stern to the bow. The length of the boat is 3 m. Calculate the distance through which the boat will move.
View SolutionTwo persons P and Q of same height are carrying a uniform beam of length 3m. If Q is at end, the distane of P from the other end so that P,Q receive loads in the ratio 5:3 is
View SolutionA uniform wooden plank of mass 150 kg and length 8 m is floating on still water with a man of 50 kg at one end of it . The man walks to the other end of the plank and stops. Than the distance covered by the plank is
View SolutionAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.
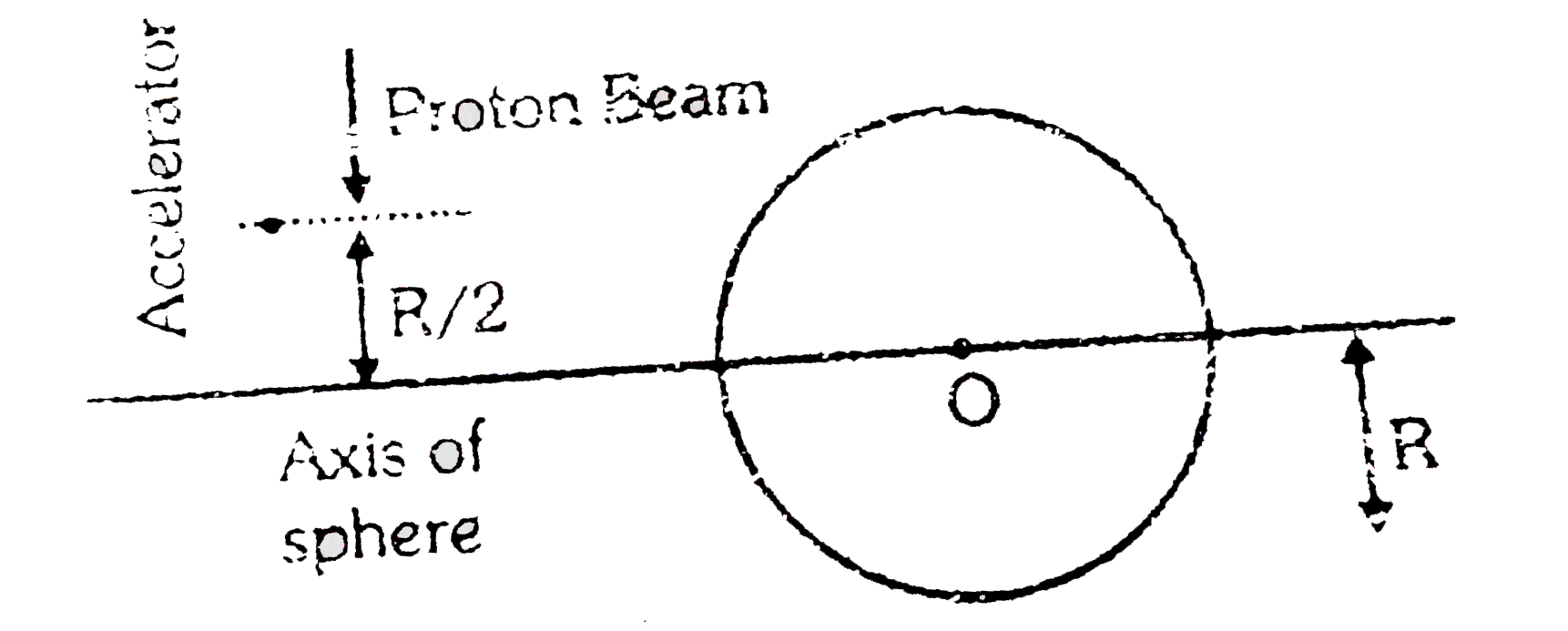
The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
One the potential of the sphere has reached its final, constant value, the minimum speed v of a proton along its trajectory path is given by
View SolutionAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.

The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
After a long time, when the potential of the sphere reaches a constant value, the trajectory of proton is correctly sketched as

View Solution

