For the given uniform square lamina , where centre is . Its moment of inertia about an axis is equal to how many times its moment of inertia about an axis ?
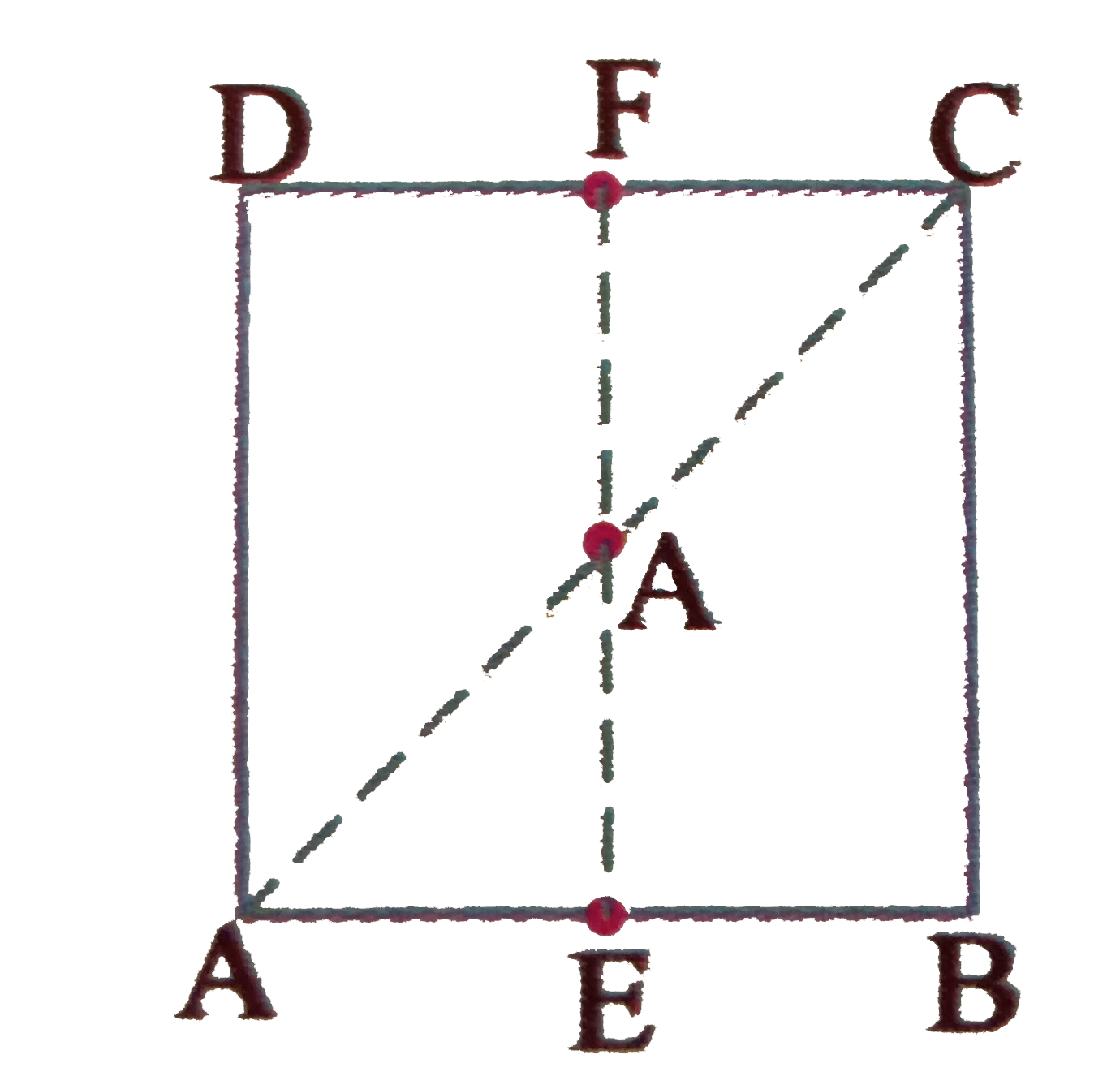
(due to symmetry)
(due to symmetry)
and
From eq(1) and (2), we get
Similar Questions
Knowledge Check
The moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
A1 IBI/2CIDI/4A solid aluminimum sphere of radius R has moment of inertia I about an axis through its centre. The moment of inertia about a central axis of a solid aluminimum sphere of radius 2R is.
A4 IB8 IC16 ID32 IA body is rotating with angular momentum L. If I is its moment of inertia about the axis of rotation is I, its kinetic energy of rotation is
A12IL2B12ILC12(I2/L)D12.L2I
Moment of inertia of a uniform circular disc about a diameter is I. Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be.
View SolutionThe moment of inertia of a circular ring about one of its diameters is I . What will be its moment of inertia about a tangent parallel to the diameter?
View SolutionMoment of inertia of a solid sphere about its diameter is I0 . Then moment of inertia about an axis parallel to its diameter at a distance equal to half of its radius is
View SolutionThere is a square planar object. Moment of inertia of this object about an axis passing through its centre and parallel to its edge is I. What will be moment of inertia about one of its diagonals?
View SolutionThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is
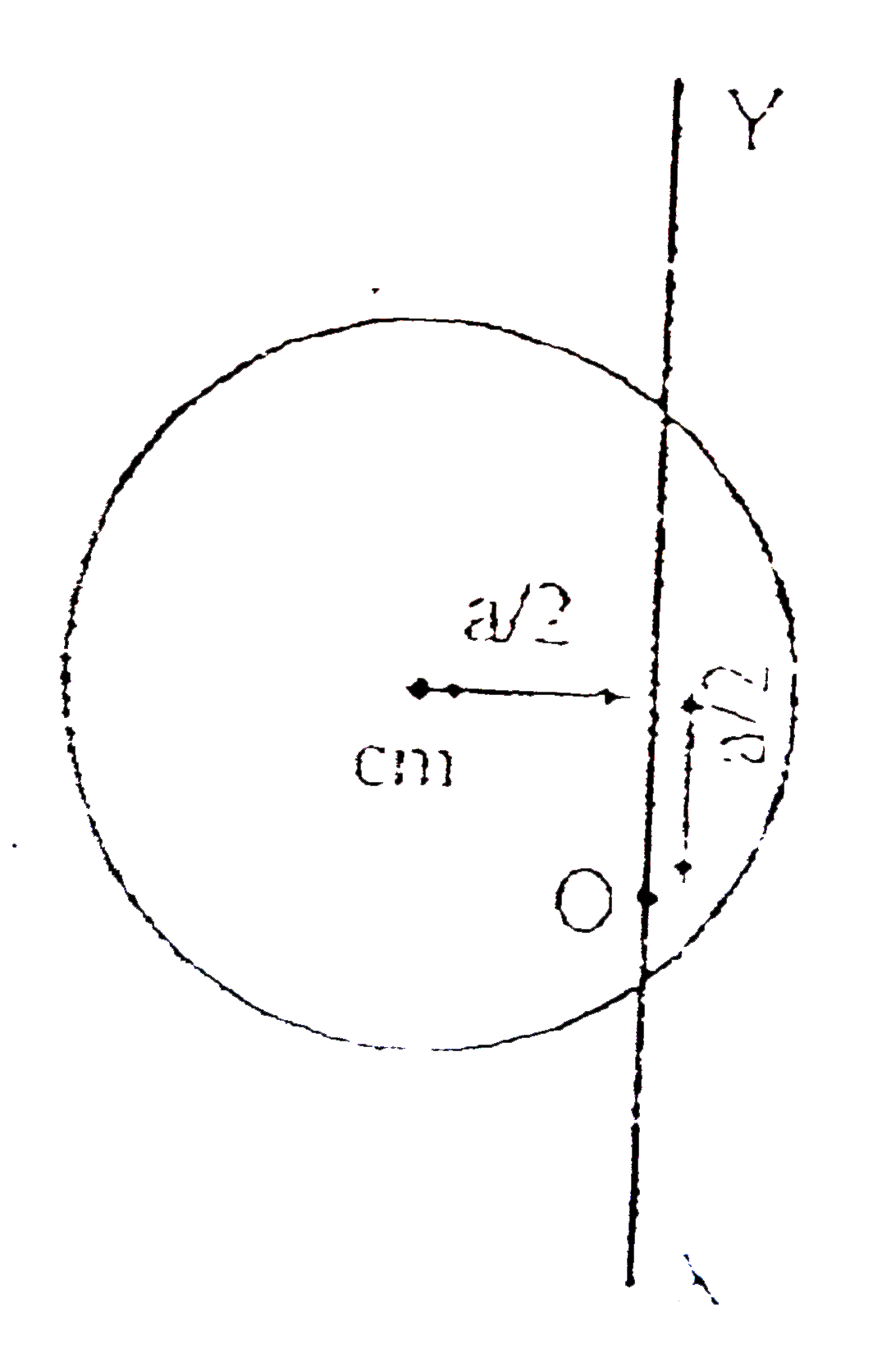
View Solution

