A uniform rod is made to lean between rough vertical wall and the ground. Friction coefficient between rod and walls is μ1=12 and between the rod and the ground is μ2=14. The rod is about to slip at contact surfaces. The correct options are:
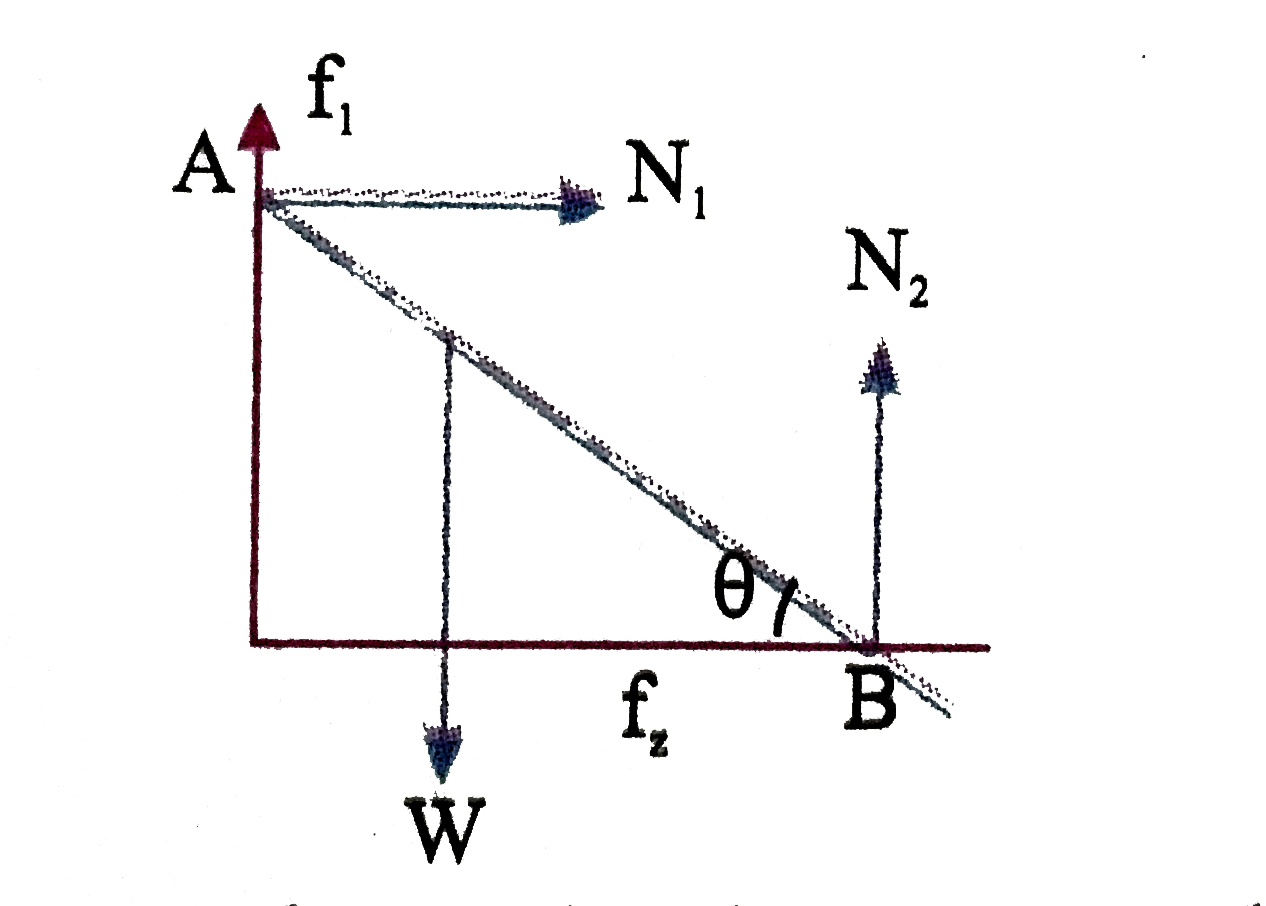
The normal reaction between rod and wall is μ2W1+μ1μ2
Normal reaction between rod and ground is W1+μ1μ2
N2>N1
N1>N2
The correct Answer is:A, B, C
For equilibrium of rod
∑Fx=0,N1=μ2N2∑Fy=0,N1=μ2W1+μ1μ2
So, choice (a) is correct. and N2=W1+μ1μ2
So, choice (b) is correct. by subsutituting the values
N1=2w9&N2=8w9∴N2>N1
Topper's Solved these Questions
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions
Explore 6 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Integer type questions
Explore 14 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Level-II (H.W)
Explore 54 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:EXERCISE -IV
Explore 40 Videos
Similar Questions
A uniform rod is made to lean between a rough vertical wall and the ground. The coefficient of friction between the rod and the ground is μ1 and between the rod and the wall is μ2. Find the angle at which the rod can he leaned without slipping.
View SolutionFind the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
View Solution
Knowledge Check
A man is running on the ground .It is known that the coefficient of friction between the man and the ground is μ . Then which of the following statements is correct
ANormal reaction between man and ground is equal to weight of manBThe direction of friction on man is in the direction of normal reaction on the manCDirection of friction on man is opposite to the direction of motion of manDMaximum acceleration of man can be 2μgA uniform rod kept vertically on the ground falls from rest. Its foot does not slip on the ground
ANo part of the rod can have acceleration greater than g in any positiveBFor any one position of the rod, different points on it have different accelerationsCThe maximum acceleration on any point on the rod, at any position, is 1.5 gDnone of theseA ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
Aθ=tan−1(μ)Bθ=tan−1(2μ)Cθ=tan−1(μ2)Dnone of these
The coefficient of friction between the wedge and the table is μ, the friction between the rod and the wedge being negligible.
View SolutionA uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

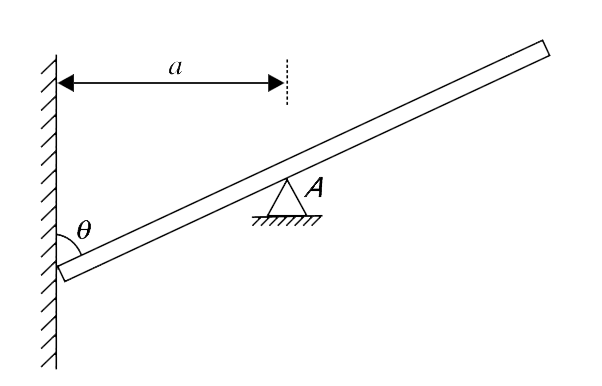
View SolutionA uniform rod of length b can be balanced as shown in figure. The lower end of the rod is resting against a vertical wall. The coefficient of friction between the rod and the wall and that between the rod and the support at A is μ. Distance of support from the wall is a.
(a) Find the ratio ab if the maximum value of θ is θ1.
(b) Find the ratio ab if the minimum value of θ is θ2.
View SolutionA uniform rod of length L rests against a smooth roller as shown in figure. Find the friction coefficient between the ground and the lower end if the minimum angle that rod can make with the horizontal is θ.

View SolutionA 60kg man is running on horizontal road with acceleration 2ms−1 friction coefficient between foot of the man and the ground is μ=0.4 then
View Solution

