A woman throws and object of mass 500g with a speed of 25ms−1. If the object hits a wall and rebounds with half the original speed, what is the change in momentum of the object?
−18.75N−S
18.75N−S
−20.75N−S
20.75N−S
The correct Answer is:A
To solve the problem, we need to calculate the change in momentum of the object when it is thrown, hits the wall, and rebounds. Here are the steps to find the solution:
Step 1: Convert mass to kilograms
The mass of the object is given as 500 grams. We need to convert this to kilograms because the standard unit of mass in physics is kilograms (kg).
Mass(m)=500g=5001000kg=0.5kg
Step 2: Calculate the initial momentum
The initial momentum (p_initial) of the object can be calculated using the formula:
pinitial=m×vinitial
Where:
- m=0.5kg
- vinitial=25m/s
Substituting the values:
pinitial=0.5kg×25m/s=12.5kg m/s
Step 3: Calculate the final velocity
The object rebounds with half the original speed. Therefore, the final speed (v_final) after rebounding is:
vfinal=252m/s=12.5m/s
Since the object is moving in the opposite direction after rebounding, we will consider this speed as negative:
vfinal=−12.5m/s
Step 4: Calculate the final momentum
The final momentum (p_final) of the object can be calculated using the same formula:
pfinal=m×vfinal
Substituting the values:
pfinal=0.5kg×(−12.5m/s)=−6.25kg m/s
Step 5: Calculate the change in momentum
The change in momentum (Δp) is given by the formula:
Δp=pfinal−pinitial
Substituting the values we calculated:
Δp=−6.25kg m/s−12.5kg m/s=−18.75kg m/s
Final Answer
The change in momentum of the object is:
Δp=−18.75kg m/s
The mass of the object is given as 500 grams. We need to convert this to kilograms because the standard unit of mass in physics is kilograms (kg).
The initial momentum (p_initial) of the object can be calculated using the formula:
- m=0.5kg
- vinitial=25m/s
The object rebounds with half the original speed. Therefore, the final speed (v_final) after rebounding is:
The final momentum (p_final) of the object can be calculated using the same formula:
The change in momentum (Δp) is given by the formula:
The change in momentum of the object is:
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:SINGLE ANSWER QUESTIONS
Explore 35 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:SINGLE ANSWER QUESTIONS Passage -1
Explore 1 Video
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -III
Explore 31 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - IV
Explore 41 Videos
Similar Questions
A woman throws an object of mass 500 g with a speed of 25ms−1 .
(a) What is the impulse imparted to the object ?
(b) If the object hitts a wall and rebounds with the half the original speed , what is the change in momentum of the object ?
View SolutionA woman throws an object of mass 500 g with a speed of 25ms−1 .
(a) What is the impulse imparted to the object ?
(b) If the object hitts a wall and rebounds with the half the original speed , what is the change in momentum of the object ?
View Solution
Knowledge Check
An object is moving in a circle at constant speed v. The magnitude of rate of change of momentum of the object.
Ais zeroBis proportional to vCis proportional to v2Dis proportional to v3A ball of mass 0.20kg falls freely from a certain height and rebounds elastically with a speed of 40ms−1. The change in momentum of the ball is
A4kgms−1B8kgms−1C16kgms−1D40kgms−1A ball of mass 'm' moves normal to a wall with a velocity 'u' and rebounds with the same speed. The change in momentum of the ball during the rebounding is
A2mu towards the wallB2mu away from the wallCzeroDmu away from the wall
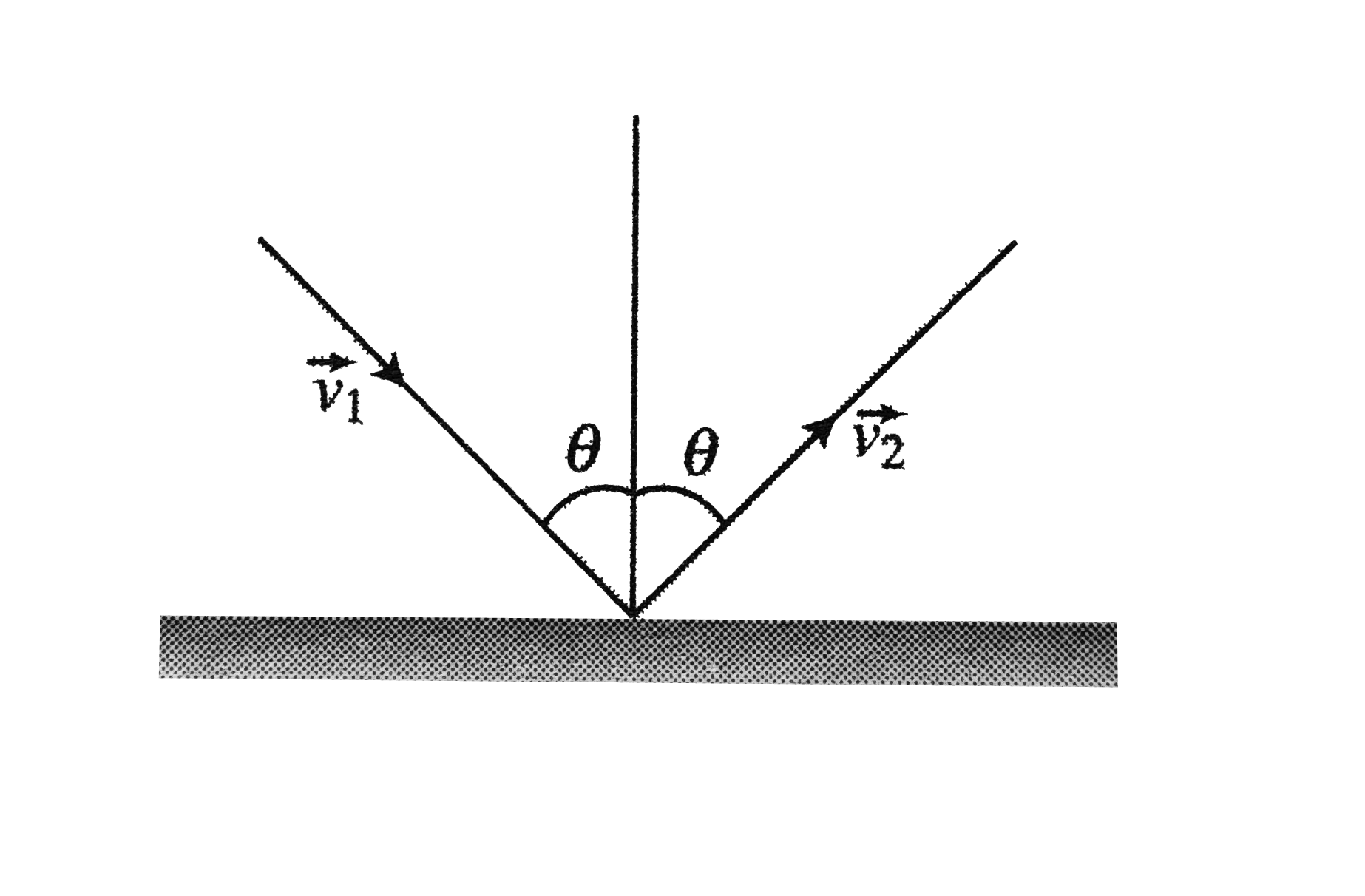
An object of m kg with speed of ms−1 strikes a wall at an angle θ and rebounds at the same speed and same angle. Find the magnitude of change in the momentum of object.
View SolutionA massless spring hangs from the ceiling with a small object attached to its lower end. The object is initially held at rest in a position y such that the spring is at its rest length. The object is then released from y and oscillates up and down, with its lowest position being 10cm below y, (a) What is the frequency of the oscillation? (b) What is the speed of the object when it is 8.0 cm below the initial position? (c ) An object of mass 600g is attached to the first object, after which the system oscillates with half the original frequency. What is the mass of the first object? (d) How far below y, is the new equilibrium (rest) position with both objects attached to the spring?
View SolutionA ball of 0.20kg hits a wall at an angle of 45∘ with a velocity of 25ms−1. If the rebounds at 90∘ to the direction of incidence, calculate the change in momentum of the ball.
View SolutionA body of mass m collides against a wall with the velocity v and rebounds with the same speed. Its magnitude of change of momentum is
View SolutionA body of mass m collides against a wall with the velocity v and rebounds with the same speed. Its magnitude of change of momentum is
View Solution

