A block of mass is placed on a rough surface with a vertical cross section of . If the coefficient of friction is , the maximum height above the ground at which the block can be placed without slipping is .
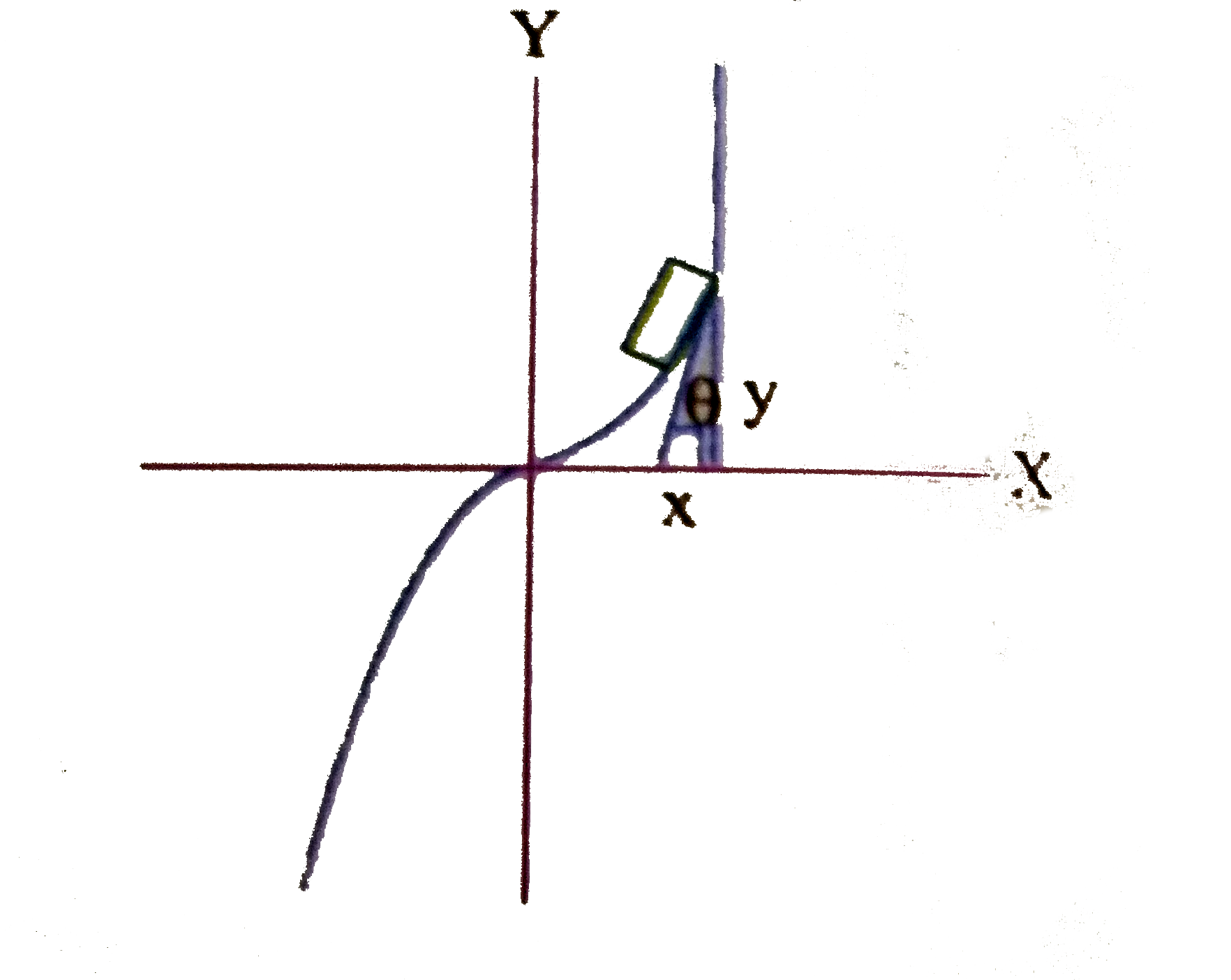
At limiting equilibrium, we get
Now putting the values of 'x' in we get
When
So the maximum height above the ground at which the block can be placed without slipping is .
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:C.U.Q
Explore 73 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -I (C.W)
Explore 47 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - IV
Explore 41 Videos
Similar Questions
A block of mass m is palced on a surface having coefficient of frictionn 0.25, with a vertical cross section given by y=x416. Calculate the maximum height above the ground t which block can be placed without slipping.
View SolutionA block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is 0.5. When

View Solution
Knowledge Check
A block of mass is placed on a surface with a vertical cross section given by y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is:
A(a) 16mB(b) 23mC(c) 13mD(d) 12mA block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
A12B√3C1√3DNoneA block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-
 A10 NB10011NC1008ND20 N
A10 NB10011NC1008ND20 N
A block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it is
View SolutionA block of mass 5 kg slides down a rough inclined surface. The angle of inclination is 45∘. The coefficient of sliding friction is 0.20. When the block slides 10 cm, the work done on the block by force of friction is
View SolutionA block is released from rest from point on a rough inclined place of inclination 37∘. The coefficient of friction is 0.5.
View SolutionA block of mass 1 kg is placed on a truck which accelerates with acceleration 5ms−2. The coefficient of static friction between the block and truck is 0.6. The frictional force acting on the block is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View Solution
