Question

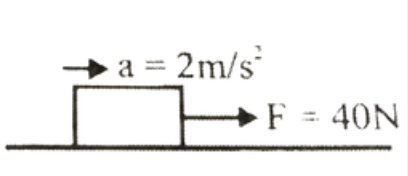
A block of mass $10kg$ is pushed by a force $F$ on a horizontal rough plane is moving with acceleration $5m{s}^{-2}$ When force is doubled its acceleration becomes $18m{s}^{-2}$ Find the coefficient of friction between the block and rough horizontal plane $(g=10m{s}^{-2})$ .

Explanation

To solve the problem, we will follow these steps:

Step 1: Identify the given data
- Mass of the block, \( m = 10 \, \text{kg} \)
- Initial acceleration, \( a_1 = 5 \, \text{m/s}^2 \)
- Final acceleration when force is doubled, \( a_2 = 18 \, \text{m/s}^2 \)
- Acceleration due to gravity, \( g = 10 \, \text{m/s}^2 \)

Step 2: Write the equations of motion
Using Newton's second law, we can write the equations for both scenarios.

1. For the initial scenario where the force is \( F \):
\( F - f_k = m \cdot a_1 \)
where \( f_k \) is the frictional force, which can be expressed as:
\( f_k = \mu_k \cdot N = \mu_k \cdot m \cdot g \)
Therefore, the equation becomes:
\( F - \mu_k \cdot m \cdot g = m \cdot a_1 \)
Substituting the values:
\( F - \mu_k \cdot 10 \cdot 10 = 10 \cdot 5 \)
Simplifying:
\( F - 100 \mu_k = 50 \quad \text{(Equation 1)} \)

2. For the second scenario where the force is doubled (\( 2F \)):
\( 2F - f_k = m \cdot a_2 \)
This gives us:
\( 2F - \mu_k \cdot m \cdot g = m \cdot a_2 \)
Substituting the values:
\( 2F - \mu_k \cdot 10 \cdot 10 = 10 \cdot 18 \)
Simplifying:
\( 2F - 100 \mu_k = 180 \quad \text{(Equation 2)} \)

Step 3: Solve the equations
Now we have two equations:
1. \( F - 100 \mu_k = 50 \) (Equation 1)
2. \( 2F - 100 \mu_k = 180 \) (Equation 2)

From Equation 1, we can express \( F \):
\( F = 50 + 100 \mu_k \)

Substituting this expression for \( F \) into Equation 2:
\( 2(50 + 100 \mu_k) - 100 \mu_k = 180 \)
Expanding:
\( 100 + 200 \mu_k - 100 \mu_k = 180 \)
This simplifies to:
\( 100 + 100 \mu_k = 180 \)
Subtracting 100 from both sides:
\( 100 \mu_k = 80 \)
Dividing by 100:
\( \mu_k = 0.8 \)

Final Answer
The coefficient of friction between the block and the rough horizontal plane is \( \mu_k = 0.8 \).

---