A body of mass is moved by a force , where x is the disatance covered Initial position is and final position is If initially the body is at rest find the final speed .
To find the final speed of a body of mass 8kg that is moved by a force F=3xN, where x is the distance covered, we will follow these steps:
Step 1: Identify the given information
- Mass of the body, m=8kg
- Force applied, F=3xN
- Initial position, xi=2m
- Final position, xf=10m
- Initial speed, u=0m/s
Step 2: Relate force to acceleration
According to Newton's second law, the force is equal to mass times acceleration:
F=m⋅a
We can express acceleration a as:
a=dvdt
Thus, we can write:
F=m⋅dvdt
Step 3: Substitute the expression for force
Substituting the expression for force:
3x=8⋅dvdt
Step 4: Use the chain rule to relate dv and dx
Using the chain rule, we can express dvdt as:
dvdt=dvdx⋅dxdt
Substituting this into the equation gives:
3x=8⋅dvdx⋅v
Step 5: Rearrange the equation
Rearranging the equation yields:
3xdx=8vdv
Step 6: Integrate both sides
Now we will integrate both sides. The left side will be integrated from x=2 to x=10, and the right side from v=0 to v:
∫1023xdx=∫v08vdv
Step 7: Calculate the integrals
Calculating the left side:
∫3xdx=3x22∣∣102=3(102)2−3(22)2=3002−122=150−6=144
Calculating the right side:
∫8vdv=4v2∣∣v0=4v2−0=4v2
Step 8: Set the integrals equal to each other
Setting the results of the integrals equal gives:
144=4v2
Step 9: Solve for v
Dividing both sides by 4:
36=v2
Taking the square root:
v=6m/s
Final Answer
The final speed of the body is 6m/s.
---
- Mass of the body, m=8kg
- Force applied, F=3xN
- Initial position, xi=2m
- Final position, xf=10m
- Initial speed, u=0m/s
According to Newton's second law, the force is equal to mass times acceleration:
F=m⋅a
We can express acceleration a as:
a=dvdt
Thus, we can write:
F=m⋅dvdt
Substituting the expression for force:
3x=8⋅dvdt
Using the chain rule, we can express dvdt as:
dvdt=dvdx⋅dxdt
Substituting this into the equation gives:
3x=8⋅dvdx⋅v
Rearranging the equation yields:
3xdx=8vdv
Now we will integrate both sides. The left side will be integrated from x=2 to x=10, and the right side from v=0 to v:
∫1023xdx=∫v08vdv
Calculating the left side:
∫3xdx=3x22∣∣102=3(102)2−3(22)2=3002−122=150−6=144
∫8vdv=4v2∣∣v0=4v2−0=4v2
Setting the results of the integrals equal gives:
144=4v2
Dividing both sides by 4:
36=v2
Taking the square root:
v=6m/s
The final speed of the body is 6m/s.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:C.U.Q
Explore 73 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -I (C.W)
Explore 47 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - IV
Explore 41 Videos
Similar Questions
An object of mass 8 kg starts to move from rest under the action of a variable force F=3xN where x is the distance (in m) covered by the object. If initially, the position of the object is x = 2 m, then find its speed (in m s−1) when it crosses x = 10 m.
View SolutionA body covers a distance of 4m under the action of force F = (17 – 4x)N where x is the distance in metres. The work done by the force is
View Solution
Knowledge Check
A body of mass m = 1 kg is moving in a medium and experiences a frictional force F = -kv, where v is the speed of the body. The initial speed is v0=10ms−1 and after 10 s, its energy becomes half of the initial energy. Then, the value of k is
A10ln√2Bln√2C120ln2D10 ln 2A body of mass 2kg is moving along north-east direction with a speed √2 m/s. A force of 0.2N is applied on the body due west for 10 sec. The final velocity ofthe body is :
A1 m/s due northB1 m/s due eastC2 m/s due northD2 m/s due east
A body covers a distance of 4m under the action of force F=(17-4x)N where x is the distance in metres. The work done by the force is
View SolutionA body of mass 5kg is acted upon by a variable force. The force varies with the distance covered by the body as shown in figure. What is the speed of the body when it has covered 25m? Assume that the body starts from rest.
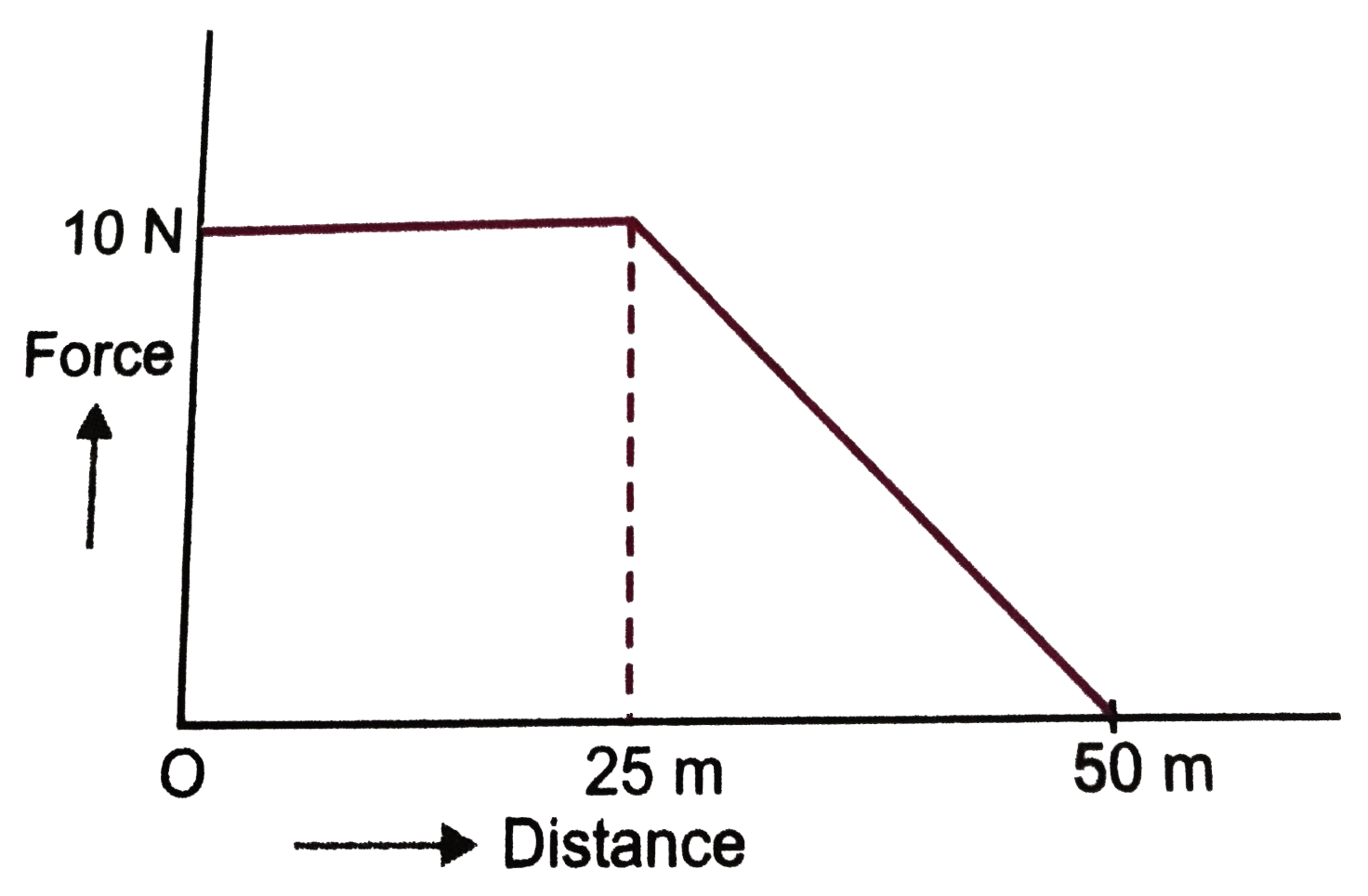
View SolutionA body covers a distance of 4m under the action of force F=(17-4x)N where x is the distance in metres.The work done by the force is
View SolutionA body covers a distance of 4m under the action of force F=(17-4x)N where x is the distance in metres.The work done by the force is
View SolutionA particle of mass m is subject to a force (F) .Find the time dependent position x(t) of the particle for the following two cases : (a) F(x)=kx, with k>0, the initial position is x0, and the initial speed is zero. (b) F(v)=−bv2 and the initial position is zero,and the initial speed is v0.
View Solution7.A particle A of mass 10/7kg is moving in the positive direction of x .Its initial position is x=0 & initial velocity is 1m/s .The velocity at x=10 is: (use the graph given)
View Solution

